Glatter Raum

Glatte normierte Räume werden im mathematischen Teilgebiet der Funktionalanalysis untersucht. Es handelt sich um normierte Räume, deren Norm eine gewisse Glattheitseigenschaft hat.

Definitionen

Es sei $(X,\|\cdot \|)$ ein normierter Raum, $B_{X}:=\{x\in X;\,\|x\|\leq 1\}$ sei die Einheitskugel und $S_{X}:=\{x\in X;\,\|x\|=1\}$ ihr Rand, die sogenannte Einheitssphäre. Nach dem Satz von Hahn-Banach gibt es zu jedem $x\in S_{X}$ ein stetiges, lineares Funktional $f_{x}\in X^{*}$ mit $\|f_{x}\|=1$ und $f_{x}(x)=1$ .

Dieses Funktional $f_{x}$ definiert die Hyperebene $\{y\in X;\,f_{x}(y)=1\}$ , die $B_{X}$ in schneidet und keinen Punkt aus dem Inneren der Einheitskugel enthält. Eine solche Hyperebene nennt man eine Stützhyperebene an , das Funktional $f_{x}$ heißt Stützfunktional an . Stellt man sich eine Hyperebene als lineare Approximation der Kugeloberfläche vor, so liegt es nahe, einen Punkt $x\in S_{X}$ einen Glattheitspunkt zu nennen, wenn es genau eine Stützhyperebene an gibt, das heißt, wenn es genau ein $f_{x}\in X^{*}$ gibt mit $\|f_{x}\|=1$ und $f_{x}(x)=1$ .

Ein normierter Raum heißt glatt, wenn jeder Punkt der Einheitssphäre ein Glattheitspunkt ist. Die Einheitskugel eines glatten Raums ist damit eine glatte konvexe Menge.

Stützabbildung

Man nennt eine Abbildung $f:X\setminus \{0\}\rightarrow X^{*}\setminus \{0\},x\mapsto f_{x}$ , eine Stützabbildung, falls folgendes gilt:

Aus $\|x\|=1$ folgt $\|f_{x}\|=f_{x}(x)=1$
Für $\lambda >0$ und $x\in X\setminus \{0\}$ gilt $f_{{\lambda x}}=\lambda f_{x}$ .

Definitionsgemäß gibt es in einem glatten Raum genau eine Stützabbildung, man kann also von der Stützabbildung eines glatten Raums sprechen. Man kann zeigen, dass diese norm-schwach*-stetig ist, das heißt stetig, wenn man auf $X\setminus \{0\}$ die Normtopologie und auf $X^{*}\setminus \{0\}$ die schwach-*-Topologie betrachtet.

Beispiele

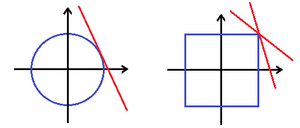
Die euklidische Norm links ist glatt, die Maximumsnorm rechts nicht.

Zweidimensionaler Raum

Glattheit hängt von der Norm ab und kann beim Übergang zu einer äquivalenten Norm verloren gehen. Das zeigt sich schon am Beispiel des zweidimensionalen Raums $\mathbb {R} ^{2}$ . Versieht man den zweidimensionalen Raum mit der euklidischen Norm $\|.\|_{2}$ , so ist die Einheitssphäre ein Kreis und jeder Punkt hat genau eine Stützhyperebene, nämlich die Tangente an diesem Punkt, das heißt $(\mathbb{R} ^{2},\|.\|_{2})$ ist glatt. Betrachtet man auf dem $\mathbb {R} ^{2}$ die Maximumsnorm $\|.\|_{\infty }$ , so ist die „Einheitskugel“ ein Quadrat. An jeder Ecke des Quadrates gibt es unendlich viele Stützhyperebenen, alle anderen Punkte sind Glattheitspunkte. Damit ein Raum glatt ist, muss aber jeder Punkt der Einheitssphäre ein Glattheitspunkt sein, das heißt $(\mathbb{R} ^{2},\|.\|_{\infty })$ ist nicht glatt. Da die euklidische Norm und die Maximumsnorm auf dem $\mathbb {R} ^{2}$ äquivalent sind, sieht man an diesem Beispiel, dass die Glattheit beim Übergang zu einer äquivalenten Norm verloren gehen kann.

Weitere Beispiele

Hilberträume sind glatt, die Stützabbildung lautet $x\mapsto f_{x}=\langle \cdot ,x\rangle$ .
Die L^p[0,1]-Räume und die Folgenräume $\ell ^{p}$ sind für $1<p<\infty$ glatt. Allgemeiner sind gleichmäßig glatte Räume glatt.
Ist ein kompakter Hausdorffraum mit mindestens zwei Punkten, so ist der Funktionenraum der stetigen Funktionen auf mit der Supremumsnorm nicht glatt.

Charakterisierungen

Folgende Aussage über einen normierten Raum $(X,\|\cdot \|)$ sind äquivalent:

$(X,\|\cdot \|)$ ist glatt.
Die Norm auf $S_{X}$ ist Gâteaux-differenzierbar, das heißt für jedes $x\in S_{X}$ und $y\in X$ existiert $\lim _{{t\searrow 0}}{\frac {\|x+ty\|-1}{t}}$ .
Jede Stützabbildung des Raums ist norm-schwach*-stetig.
Es gibt eine norm-schwach*-stetige Stützabbildung.
Für jedes $x\in S_{X}$ und jede Folge $(\varphi _{n})_{{n\in \mathbb{N} }}$ in $S_{{X^{*}}}$ mit $\varphi _{n}(x)\rightarrow 1$ folgt, dass $(\varphi _{n})_{{n\in \mathbb{N} }}$ schwach*-konvergiert.
Jeder zwei-dimensionale Unterraum ist glatt.
Die Orthogonalität ist rechts-additiv, das heißt aus $x\perp y$ und $x\perp z$ folgt $x\perp (y+z)$ .

Dualität

Über die Dualität besteht ein enger Zusammenhang zur strikten Konvexität.

Ein normierter Raum $(X,\|\cdot \|)$ ist glatt, falls sein Dualraum strikt konvex ist.
Ein normierter Raum $(X,\|\cdot \|)$ ist strikt konvex, falls sein Dualraum glatt ist.

Die Umkehrungen gelten im Allgemeinen nicht.

Renormierbarkeit

Da die Glattheit beim Übergang zu einer äquivalenten Norm verloren gehen kann, stellt sich in natürlicher Weise die Frage, zu welchen normierten Räumen es äquivalente, glatte Normen gibt, die also durch Übergang zu einer äquivalenten Norm glatt werden. Solche Räume nennt man glatt renormierbar.

Reflexive Räume sind strikt konvex renormierbar und daher wegen obiger Dualitätseigenschaften auch glatt renormierbar, sogar glatt und gleichzeitig strikt konvex renormierbar. Das gilt allgemeiner für schwach kompakt erzeugte Räume.

$\ell ^{\infty }$ ist nicht glatt renormierbar.

Basierend auf einem Artikel in:

Wikipedia.de