
Neilsche Parabel

Die Neil’sche Parabel (nach dem englischen Mathematiker William Neile benannt) oder semikubische Parabel ist eine spezielle ebene algebraische Kurve, die durch eine Gleichung der Form
- (A)
beschrieben werden kann. Auflösen nach
ergibt die explizite Form
- (E1)
die Anlass für die Bezeichnung semikubische Parabel liefert.
(Eine gewöhnliche Parabel kann durch eine Gleichung
beschrieben werden.)
Löst man (A) nach
auf, so erhält man die Gleichung
- (E2)
Mit Hilfe der ersten Gleichung erkennt man, dass
- (P)
eine Parameterdarstellung der Neilschen Parabel ist.
William Neile hatte erstmals die Bogenlänge dieser Kurve berechnet, die sog. Rektifikation, und dies 1657 bekannt gemacht. Aufgrund der Probleme bei der Rektifizierung von Ellipsen und Parabeln vermutete man zu dieser Zeit, dass der Kreis und die Gerade die einzigen rektifizierbaren algebraischen Kurven seien.
Die Neil’sche Parabel ist rational, es existiert also eine rationale Abbildung mit einer inversen rationalen Abbildung, die die Neil'sche Parabel auf die projektive Gerade abbildet.
Eigenschaften einer Neilschen Parabel
Ähnlichkeit
- Jede Neilsche Parabel
ist zur Neilschen Einheitsparabel
ähnlich.
Beweis: Die Ähnlichkeitsabbildung
(Streckung am Ursprung) führt die Neilsche Parabel
in die Kurve
mit
über.
Singularität
- Die Parameterdarstellung
ist überall außer im Punkt
regulär. Die Kurve besitzt im Nullpunkt eine Singularität (Spitze).
Der Beweis folgt aus dem Tangentenvektor .
Nur für
ergibt sich der Nullvektor.

Tangenten
Für die Neilsche Einheitsparabel
ergibt sich durch Differentiation die Gleichung der Tangente in einem Punkt
des oberen Astes:
Diese Tangente schneidet die Kurve in genau einem weiteren Punkt des unteren Astes mit den Koordinaten
(Beim Nachrechnen sollte man berücksichtigen, dass
ein doppelter Schnittpunkt der Tangente mit der Kurve ist.)
Bogenlänge
Um die Bogenlänge einer parametrisierten Kurve
zu bestimmen, muss man das unbestimmte Integral
lösen. Für die Neilsche Parabel
ist
(Das Integral lässt sich mit Hilfe der Substitution
lösen.)
Beispiel: Für
(Neilsche Einheitsparabel) und der oberen Grenze
,
d.h. bis zum Punkt
,
ist die Länge
.
Evolute der Einheitsparabel
- Die Evolute
der Parabel
ist eine in x-Richtung um 1/2 verschobene Neilsche Parabel:
Polarkoordinaten
Um die Darstellung der Neilschen Parabel
in Polarkoordinaten zu finden, schneidet man die Ursprungsgerade
mit der Kurve. Für
gibt es einen vom Nullpunkt (Spitze) verschiedenen Punkt:
.
Der Abstand dieses Punktes zum Nullpunkt ist
.
Mit
und
ergibt sich
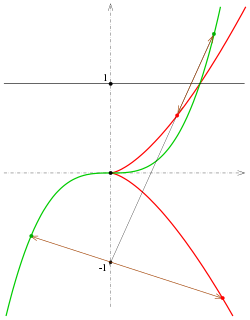
Projektive Äquivalenz zur kubischen Parabel
Bildet man die Neilsche Einheitsparabel
mit der projektiven Abbildung
(involutorische Perspektivität
mit der Achse
und Zentrum
) ab, so erhält man die Kurve
,
also die kubische
Parabel
.
Die Spitze (Nullpunkt) der Neilschen Parabel wird mit dem Fernpunkt der y-Achse
vertauscht.
Diese Eigenschaft lässt sich auch an der Darstellung der Neilschen Parabel in
homogenen
Koordinaten erkennen: Ersetzt man in (A)
(die Ferngerade hat die Gleichung
)
und multipliziert mit
erhält man die Kurvengleichung
- in homogenen Koordinaten:
Wählt man nun die Gerade
als Ferngerade und setzt
erhält man die (affine) Kurve


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 11.09. 2021