
Pythagoreische Primzahl
In der Zahlentheorie
ist eine pythagoreische Primzahl
(vom englischen pythagorean prime) eine Primzahl
der Form
mit
(nicht zu verwechseln mit Pythagoraszahl).
Ist eine Primzahl keine pythagoreische Primzahl, so heißt sie
nicht-pythagoreische Primzahl.
Beispiele
- Die kleinsten pythagoreischen Primzahlen sind die folgenden:
- 5, 13, 17, 29, 37, 41, 53, 61, 73, 89, 97, 101, 109, 113, 137, 149, 157,
173, 181, 193, 197, 229, 233, 241, 257, 269, 277, 281, 293, 313, 317, 337,
349, 353, 373, 389, 397, 401, 409, 421, 433, 449, 457, 461, 509, 521, 541,
557, 569, 577, 593, 601, 613, 617, … (Folge
 A002144 in OEIS)
A002144 in OEIS)
Eigenschaften
- Jede pythagoreische Primzahl kann als Summe von zwei Quadraten dargestellt werden.
-
- Beweis:
- Der Beweis folgt direkt aus Fermatschem Satz über die Summe von zwei Quadraten. Gelegentlich nennt man diesen Satz auch Girard’s Theorem.
- Beispiel:
,
, …
- Beweis:
- Die Umkehrung der obigen Eigenschaft gilt ebenfalls:
- Ist die Summe von zwei Quadraten eine ungerade Primzahl, so ist sie eine
pythagoreische Primzahl.
- Beweis:
- Der Beweis folgt ebenfalls direkt aus Fermatschem Satz über die Summe von zwei Quadraten:
- Für das Quadrat einer geraden Zahl
mit
gilt:
.
- Für das Quadrat einer ungeraden Zahl
mit
gilt:
.
- Für ungerade Primzahlen
gilt:
(für pythagoreische Primzahlen) oder
(für nicht-pythagoreische Primzahlen).
- Die Summe von zwei Quadratzahlen ist aus obigen Gründen immer
,
oder
, aber niemals
. Ist sie also eine ungerade Primzahl, so bleibt nur
übrig und das sind genau die pythagoreischen Primzahlen.
- Beweis:
- Für jede pythagoreische Primzahl
gibt es ein rechtwinkliges Dreieck mit Hypotenusenlänge
, welches ganzzahlige Kathetenlängen hat.
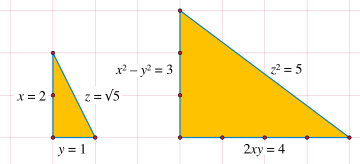
Die
pythagoreische Primzahl  und seine Quadratwurzel als Hypotenusen von rechtwinkligen Dreiecken und wie man
aus dem kleinen Dreieck das große berechnen kann
und seine Quadratwurzel als Hypotenusen von rechtwinkligen Dreiecken und wie man
aus dem kleinen Dreieck das große berechnen kann
-
- Beweis:
- Siehe Satz des Pythagoras
- Beweis:
- Ist die Primzahl
die Hypotenusenlänge eines rechtwinkligen Dreiecks, so ist
eine pythagoreische Primzahl und größter Teil eines pythagoreischen Tripels.
- Es gibt unendlich viele pythagoreische Primzahlen.
-
- Beweis:
Das Primrennen zwischen 4n+1 und 4n+3
Sei .
Dann gilt:
- Die Anzahl der pythagoreischen Primzahlen (der Form
) bis
ist annähernd gleich wie die Anzahl der nicht-pythagoreischen Primzahlen (der Form
) bis
. Im Speziellen ist die Anzahl der pythagoreischen Primzahlen bis
oft etwas kleiner. Dieses Phänomen nennt man auf Englisch Chebyshev's bias und stammt vom Mathematiker Pafnuti Lwowitsch Tschebyschow.
Beispiele
- Bis
gibt es nur zwei Zahlen, unter denen mehr pythagoreische Primzahlen (der Form
) als nicht-pythagoreische (ungerade) Primzahlen (der Form
) existieren, nämlich
und
. Zwischen
und
sind es gleich viele und ab
gibt es wieder mehr nicht-pythagoreische (ungerade) Primzahlen.
- Die folgende Liste zeigt an, wann ein „Führungswechsel“ im „Rennen“ pythagoreische Primzahlen gegen nicht-pythagoreische (ungerade) Primzahlen stattfindet (auf englisch Where prime race 4n-1 vs. 4n+1 changes leader):
- 3, 26861, 26879, 616841, 617039, 617269, 617471, 617521, 617587, 617689,
617723, 622813, 623387, 623401, 623851, 623933, 624031, 624097, 624191,
624241, 624259, 626929, 626963, 627353, 627391, 627449, 627511, 627733,
627919, 628013, 628427, 628937, 629371, … (Folge
 A007350 in OEIS)
A007350 in OEIS)
Zusammenhang mit Gaußschen Primzahlen
Die Norm
einer Gaußschen
Zahl der Form
ist
.
Es gilt:
- Eine pythagoreische Primzahl (inklusive der Primzahl
) kann immer als Norm einer Gaußschen ganzen Zahl dargestellt werden. Ungerade nicht-pythagoreische Primzahlen können das nicht.
- Eine pythagoreische Primzahl ist keine Primzahl in der Menge der
Gaußschen Primzahlen. Der Realteil
und der Imaginärteil
ihrer Primfaktoren in dieser Faktorisierung sind die Kathetenlängen des rechtwinkligen Dreiecks mit gegebener Hypotenusenlänge
.
-
- Beweis:
- Es kann jede pythagoreische Primzahl
zerlegt werden in
.
- Es kann jede pythagoreische Primzahl
- Beweis:
- Vergleiche dazu auch die Gruppe der rationalen Punkte auf dem Einheitskreis.
Quadratische Reste
- Seien
zwei verschiedene ungerade Primzahlen, wobei mindestens eine der beiden eine pythagoreische Primzahl sein soll. Dann gilt:
-
ist quadratischer Rest modulo
genau dann, wenn
quadratischer Rest modulo
ist.
- Mit anderen Worten:
- Seien
mit
und
. Dann gilt mit dem Legendre-Symbol:
- Beispiel:
- Sei
und
. Dann ist
und somit ist
quadratischer Rest modulo
. Umgekehrt ist
und somit ist
quadratischer Rest modulo
.
- Sei
- Seien
zwei verschiedene ungerade Primzahlen, wobei beide nicht-pythagoreische Primzahlen sein sollen. Dann gilt:
-
ist quadratischer Rest modulo
genau dann, wenn
kein quadratischer Rest modulo
ist.
- Mit anderen Worten:
- Seien
mit
und
. Dann gilt:
- Beispiel:
- Sei
und
. Dann ist
und somit ist
quadratischer Rest modulo
. Umgekehrt gibt es aber kein
mit
und somit ist
kein quadratischer Rest modulo
.
- Sei
Siehe auch
Quadratisches Reziprozitätsgesetz


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 23.08. 2022