Pythagoreisches Tripel

Kleinstes Tripel: $(3,\ 4,\ 5)$

In der Zahlentheorie wird ein pythagoreisches Tripel oder pythagoreisches Zahlentripel von drei natürlichen Zahlen gebildet, die als Längen der Seiten eines rechtwinkeligen Dreiecks vorkommen können. Mit den Seitenlängen eines solchen Dreiecks kann auf einfache Weise ein rechter Winkel konstruiert werden, beispielsweise mit dem kleinsten Tripel $(3,\ 4,\ 5)$ . Wegen des pythagoreischen Lehrsatzes sind diese Tripel genau die positiven ganzzahligen Lösungen der diophantischen Gleichung

$a^{2}+b^{2}=c^{2}$ .

Wenn , und außer 1 keinen Teiler gemeinsam haben, spricht man von einem primitiven pythagoreischen Tripel.

Geschichte

Die Tontafel Plimpton 322

Pythagoreische Tripel finden sich bereits auf babylonischen Tontafeln, die in die Zeit der Hammurabi-Dynastie datiert werden (1829 bis 1530 v.Chr.). Die Keilschrifttafel Plimpton 322 enthält 15 verschiedene pythagoreische Tripel, u.a. (56,90,106) , (119, 120, 169) und (12709, 13500, 18541) , was darauf schließen lässt, dass bereits vor mehr als 3500 Jahren ein Verfahren zur Berechnung solcher Tripel bekannt war. Für Ägypten ist die explizite Erwähnung von pythagoreischen Tripeln nur aus einem demotischen Papyrus des 3. Jahrhunderts v.Chr. bekannt, doch wurde auch die Verwendung insbesondere der Tripel $(3,\ 4,\ 5)$ und $(20,\ 21,\ 29)$ für Böschungswinkel bei einigen Pyramiden aus einer Zeit rund zweitausend Jahre vor dem erwähnten Papyrus diskutiert.

Das indische Baudhayana-Sulbasutra aus dem 6. Jahrhundert vor Christus enthält fünf pythagoreische Tripel.

Pythagoreische Tripel wurden bei den Griechen von Euklid, nach dem Kommentar von Proklos zu Euklids Elementen von Pythagoras und Platon behandelt und später von Diophant.

Beispiele

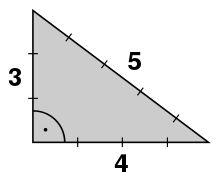
$(3,\ 4,\ 5)$ ist das kleinste und bekannteste pythagoreische Tripel. Es ist primitiv, denn die drei natürlichen Zahlen haben nur 1 als Teiler gemeinsam. Im Gebrauch einer Zwölfknotenschnur lässt sich mit den Proportionen 3:4:5 für die Seitenlängen ein rechtwinkliges Dreieck aufspannen und somit ein rechter Winkel darstellen.
$(5,\ 12,\ 13)$ und $(8,\ 15,\ 17)$ sind Beispiele für weitere kleine primitive pythagoreische Tripel.
Beispiele für nicht primitive pythagoreische Tripel sind $(15,\ 20,\ 25)$ mit als einem gemeinsamen Teiler oder $(15,\ 36,\ 39)$ mit dem gemeinsamen Teiler .

Erzeugung der pythagoreischen Tripel

Pythagoreische Tripel im kartesischen Koordinatensystem mit x und y von 1 bis 2500. Die deutlich dunklen Linien markieren Tripel der Form $(3n,\ 4n,\ 5n).$ Die Symmetrie zur 45°-Achse ist eine Folge des Kommutativgesetzes.

Die drei Formeln

$a=m^{2}-n^{2}$

$b=2\;\!mn$

$c=m^{2}+n^{2}$

liefern für beliebige $m,n\in \mathbb {N} ,m>n>0$ ein pythagoreisches Tripel $(a,\ b,\ c)$ . Es ist genau dann primitiv, wenn und teilerfremd und nicht beide ungerade sind.

Diese Formeln wurden von Euklid angegeben (Elemente, Buch 10, Proposition 29, Lemma 1). Sie werden manchmal indische Formeln genannt, da sie explizit auch vom indischen Mathematiker Brahmagupta (598–668) knapp 900 Jahre später angegeben wurden. Möglicherweise waren sie auch den Babyloniern bekannt bei ihrer Erstellung pythagoreischer Tripel, denn die Formeln ergeben sich unmittelbar aus der babylonischen Multiplikationsformel

$k\cdot l={\left({\frac {k+l}{2}}\right)\!}^{2}-{\left({\frac {k-l}{2}}\right)\!}^{2},$

wenn man $k=m^{2}$ und $l=n^{2}$ setzt und mit $2^{2}$ multipliziert: $\quad (2\;\!mn)^{2}=\left(m^{2}+n^{2}\right)^{2}-\left(m^{2}-n^{2}\right)^{2}$ .

Umgekehrt lässt sich jedes primitive pythagoreische Tripel $(a,\ b,\ c)$ mit Hilfe dieser Formeln aus teilerfremden $m,n\in \mathbb {N}$ erzeugen.

Jedes pythagoreische Tripel (A, B, C) kann aus einem primitiven pythagoreischen Tripel durch $(A,B,C)=(Na,Nb,Nc)$ berechnet werden. Die natürliche Zahl ist der größte gemeinsame Teiler von $A,\ B,\ C$ und damit eindeutig bestimmt.

Beispiele:

$m=2,\ n=1$ liefert das Tripel $(3,\ 4,\ 5)$ .
Multiplikation mit liefert $(6,\ 8,\ 10)$ . Es ergibt sich auch nach der babylonischen Multiplikationsformel aus $k=3,\ l=1.$ Weil und beide ungerade sind, ist es nicht primitiv.
$m=3,\ n=2$ liefert das primitive Tripel $(5,\ 12,\ 13)$ .
Multiplikation mit $N=7$ liefert $(35,\ 84,\ 91)$ ; dies ist ein pythagoreisches Tripel, das sich nicht mit den Formeln nach Euklid erzeugen lässt. Diese erzeugen zwar alle primitiven, aber nur einen Teil der nicht-primitiven Tripel.

Die Verbindung der von B. Berggren (1934) und von A. Hall (1970) bekannten Baumstruktur der primitiven pythagoreischen Tripel mit der modularen Gruppe untersuchte R. C. Alperin (2005). Sämtliche primitiven pythagoreischen Tripel lassen sich über sieben verschiedene Lineartransformationen, jeweils ausgehend von $(3,4,5)$ , in (bis auf die Anordnung) genau drei verschiedenen ternären Wurzelbäumen erzeugen, wie Firstov allgemein bewies. Genau ein Wurzelbaum hat mit einem anderen jeweils eine Lineartransformation gemeinsam, eine davon erzeugt bspw. alle (primitiven) pythagoreischen Tripel $(x,\ y,\ y+1)$ , auch alle mit einer beliebigen ungeraden Primzahl , und der von Price entdeckte andere Wurzelbaum die beiden (gemischten) Darstellungen $(p'q',\ 2pq,\ pq'+qp')$ und $(p'q',\ 2pq,\ pq'-qp')$ der primitiven Tripel mit ungeradem $q$ , einem dazu teilerfremden und $p=q'+q,\ p'=q+p$ .

Herleitung der Formel zur Bildung der pythagoreischen Tripel

Ist (a,b,c) ein pythagoreisches Tripel, so ergibt die Division der zugehörigen Gleichung $a^{2}+b^{2}=c^{2}$ durch $c^{2}$

$\left({\frac {a}{c}}\right)^{2}+\left({\frac {b}{c}}\right)^{2}=1$ .

Die Zahlen $x:={\tfrac {a}{c}}$ und $y:={\tfrac {b}{c}}$ sind rational und positiv und erfüllen die Koordinatengleichung des Einheitskreises

$x^{2}+y^{2}=1$ .

Also ist (x,y) ein Punkt mit rationalen Koordinaten auf dem Einheitskreis. Die Gerade durch die Punkte (-1,0) und (x,y) schneidet die -Achse in einem Punkt (0,t) , wobei die Steigung dieser Geraden ist, für die gilt:

$t={\frac {y}{x+1}}$

Daher ist eine rationale Zahl.

Eliminiert man aus dieser Gleichung und der des Einheitskreises, erhält man mit

${\begin{aligned}x^{2}+t^{2}(x+1)^{2}&=1\\(x^{2}-1)+t^{2}(x+1)^{2}&=0\\(x+1)\left[(x-1)+t^{2}(x+1)\right]&=0\end{aligned}}$

eine Bestimmungsgleichung für .

Wegen x>0 gilt $x+1\neq 0$ , sodass man beide Seiten durch (x+1) dividieren darf:

${\begin{aligned}(x-1)+t^{2}(x+1)&=0\\x&={\frac {1-t^{2}}{1+t^{2}}}\\y&=t\cdot (x+1)=t\cdot \left({\frac {1-t^{2}}{1+t^{2}}}+1\right)={\frac {2t}{1+t^{2}}}\end{aligned}}$

Damit haben wir also

$(x,y)=\left({\frac {1-t^{2}}{1+t^{2}}},{\frac {2t}{1+t^{2}}}\right)$

oder, weil man $t={\tfrac {v}{u}}$ mit teilerfremden natürlichen Zahlen u,v setzen kann:

$\left({\frac {a}{c}},{\frac {b}{c}}\right)=\left({\frac {1-{\frac {v^{2}}{u^{2}}}}{1+{\frac {v^{2}}{u^{2}}}}},{\frac {\frac {2v}{u}}{1+{\frac {v^{2}}{u^{2}}}}}\right)=\left({\frac {u^{2}-v^{2}}{u^{2}+v^{2}}},{\frac {2uv}{u^{2}+v^{2}}}\right)$

Dies ergibt das pythagoreische Tripel

$(a,b,c)=(u^{2}-v^{2},2uv,u^{2}+v^{2}).$

Es kann vorkommen, dass $u^{2}-v^{2}$ , 2uv und $u^{2}+v^{2}$ einen gemeinsamen Teiler N > 1 haben. Aus $u=3,\ v=1$ würde beispielsweise $a=8,\ b=6,\ c=10$ folgen.

Als einzige Möglichkeit hierfür kommt jedoch N=2 in Betracht. Denn angenommen, eine ungerade Primzahl teilte sowohl $u^{2}-v^{2}$ als auch $u^{2}+v^{2}$ , so wäre

$v^{2}\equiv u^{2}{\pmod {p}}$ und $v^{2}\equiv -u^{2}{\pmod {p}},$

woraus man, weil prim und teilerfremd zu ist, so weiter schließen kann:

${\begin{aligned}u^{2}&\equiv -u^{2}{\pmod {p}}\\2u^{2}&\equiv 0\quad \ {\pmod {p}}\\u^{2}&\equiv 0\quad \ {\pmod {p}}\\u&\equiv 0\quad \ {\pmod {p}}\\\end{aligned}}$

Die ungerade Primzahl teilt also und wegen $v^{2}\equiv u^{2}{\pmod {p}}$ auch . Das steht jedoch in Widerspruch zur Teilerfremdheit von und , sodass nicht ungerade sein kann. Also bleibt nur N=2 , was mit $u\equiv v\equiv 1{\pmod {2}}$ offenbar auch tatsächlich möglich und immer der Fall ist.

Man kann solche u,v , die teilerfremd und beide ungerade sind, jedoch aussortieren, ohne primitive pythagoreische Tripel zu verlieren. Denn, wenn und das Tripel (2a,2b,2c) ergeben, so ergeben $u'=(u+v)/2$ und $v'=(u-v)/2$ das Tripel (b,a,c) . Dabei sind u',v' teilerfremd und nicht beide ungerade.

Weitere Formeln für pythagoreische Tripel

Aus der Antike stammen nach Proklos die Formeln von Pythagoras und Plato.

Pythagoras gibt die Seitenlängen

$a=k,\ b={\frac {k^{2}-1}{2}},\ c={\frac {k^{2}+1}{2}}$

für ungerades $k\geq 3$ an. Plato gibt die Seitenlängen

$a=l,\ b={\left({\frac {l}{2}}\right)}^{\!2}\!\!-1,\ c={\left({\frac {l}{2}}\right)}^{\!2}\!\!+1$

für gerade $l\geq 4$ an.

Setzt man $k=2n+1$ mit $1\leq n\in \mathbb {N}$ , ergibt die Formel von Pythagoras

$(2n+1,\ 2n^{2}+2n,\ 2n^{2}+2n+1)$ .

Die Formel für Plato ergibt für $l=2n$ mit $2\leq n\in \mathbb {N}$

$(2n,\ n^{2}-1,\ n^{2}+1)$ .

Primitive pythagoreische Tripel

Primitive pythagoreischen Tripel $(a,\ b,\ c)$ sind solche, für die a,b und keinen gemeinsamen Teiler außer 1 haben (diese drei Zahlen sind dann auch paarweise teilerfremd).

Die größte Zahl ist ungerade, von den Zahlen und ist jeweils eine gerade und eine ungerade.
Für jeden Primfaktor von $|b-a|$ gilt: $\quad p\equiv \pm 1{\pmod {8}}$ .
Für jeden Primfaktor des Quadrats der Kathetenhalbierenden $a^{2}+({\tfrac {b}{2}})^{2}$ gilt: $\quad p\equiv 1{\pmod {12}}$ .
Das Produkt $a\!\cdot \!b\!\cdot \!c$ aller drei Zahlen ist immer durch 60 teilbar.

Beispiele primitiver pythagoreischer Tripel

Nach den Euklidischen Regeln erhält man als primitive pythagoreische Tripel zum Beispiel (aufsteigend geordnet nach m+n und bei Gleichheit dann nach der kleineren Zahl ):

m	n	a	b	c	m	n	a	b	c
2	1	3	4	5	7	2	45	28	53
4	1	15	8	17	5	4	9	40	41
3	2	5	12	13	10	1	99	20	101
6	1	35	12	37	9	2	77	36	85
5	2	21	20	29	8	3	55	48	73
4	3	7	24	25	7	4	33	56	65
8	1	63	16	65	6	5	11	60	61

Die primitiven pythagoreischen Tripel mit $c<300$ (aufsteigend geordnet nach der größten der drei Zahlen und bei Gleichheit dann nach der kleinsten) sind:

(3, 4, 5)	(5, 12, 13)	(8, 15, 17)	(7, 24, 25)
(20, 21, 29)	(12, 35, 37)	(9, 40, 41)	(28, 45, 53)
(11, 60, 61)	(16, 63, 65)	(33, 56, 65)	(48, 55, 73)
(13, 84, 85)	(36, 77, 85)	(39, 80, 89)	(65, 72, 97)
(20, 99, 101)	(60, 91, 109)	(15, 112, 113)	(44, 117, 125)
(88, 105, 137)	(17, 144, 145)	(24, 143, 145)	(51, 140, 149)
(85, 132, 157)	(119, 120, 169)	(52, 165, 173)	(19, 180, 181)
(57, 176, 185)	(104, 153, 185)	(95, 168, 193)	(28, 195, 197)
(84, 187, 205)	(133, 156, 205)	(21, 220, 221)	(140, 171, 221)
(60, 221, 229)	(105, 208, 233)	(120, 209, 241)	(32, 255, 257)
(23, 264, 265)	(96, 247, 265)	(69, 260, 269)	(115, 252, 277)
(160, 231, 281)	(161, 240, 289)	(68, 285, 293)

Bemerkenswertes

Zwei Folgen von pythagoreischen Tripeln sind noch bemerkenswert:

$m=k+1$ und $n=k\quad (1\leq k\in \mathbb {N} )$ ergibt mit $(m^{2}-n^{2},\ 2\;\!mn,\ m^{2}+n^{2})$

$(3,4,5),\;(5,12,13),\;(7,24,25),\;(9,40,41),\;(11,60,61),\;(13,84,85),\;\dotsc ,\;(2k+1,\ 2k^{2}+2k,\ 2k^{2}+2k+1),\ \dotsc$

für jede Zahl ein Tripel, das die ungerade Zahl 2k+1

(als kleinste Zahl) enthält und bei dem sich die beiden anderen Zahlen um genau unterscheiden.

Der Halbumfang eines rechtwinkeligen Dreiecks mit diesen Seitenlängen beträgt $s=2n^{2}+3n+1$ .

$m=2k\quad (1\leq k\in \mathbb {N} )$ und ergibt mit $(m^{2}-n^{2},\ 2\;\!mn,\ m^{2}+n^{2})$

$(3,4,5),\;(15,8,17),\;(35,12,37),\;(63,16,65),\;(99,20,101),\;(143,24,145),\;\dotsc ,(4k^{2}-1,\ 4k,\ 4k^{2}+1),\ \dotsc$

für die durch 4 teilbare Zahl ein Tripel, das (als kleinste Zahl, außer für k=1

, dort ist es die mittlere Zahl) enthält und bei dem sich die beiden anderen Zahlen um genau unterscheiden.

Der Halbumfang eines rechtwinkeligen Dreiecks mit diesen Seitenlängen beträgt $s=4n^{2}+2n$ .

Auch in dem noch fehlenden Fall $2\cdot (2n+1)$ des Doppelten einer ungeraden Zahl findet man leicht immer ein (natürlich nicht primitives) pythagoreisches Tripel, indem man die Lösungen der ersten Folge einfach zu $(4n+2,4n^{2}+4n,4n^{2}+4n+2)$ verdoppelt. Somit kann man zu jeder natürlichen Zahl $x>2$ ein Zahlenpaar (b,c) finden, mit dem sich zu einem pythagoreischen Tripel $(x,\ y,\ z)$ ergänzen lässt – bei ungeradem mit der Differenz 1, bei geradem mit Differenz 2:

a	b	c	a	b	c	a	b	c
3	4	5	11	60	61	19	180	181
4	3	5	12	35	37	20	99	101
5	12	13	13	84	85	21	220	221
*6	8	10	*14	48	50	*22	120	122
7	24	25	15	112	113	23	264	265
8	15	17	16	63	65	24	143	145
9	40	41	17	144	145	25	312	313
*10	24	26	*18	80	82	*26	168	170

Mit * sind nichtprimitive Tripel markiert. Diese Fälle für $a=4n+2$ sind redundant, da sie auch durch Verdoppelung von $a=2n+1$ entstehen.

Alternative Formel zur Erzeugung primitiver pythagoreischer Tripel

Die babylonischen Multiplikationsformel

$a=kl$

$b={\frac {k^{2}-l^{2}}{2}}$

$c={\frac {k^{2}+l^{2}}{2}}$

liefern für teilerfremde ungerade $k,l\in \mathbb {N}$ mit $k>l$ ein primitives pythagoreisches Tripel.

Höhe primitiver pythagoreischer Tripel

Primitive pythagoreische Tripel $((1+2i)(1+2j),2(i-j)(1+i+j),(i-j)^{2}+(1+i+j)^{2})$ mit $i,j\in \mathbb {N} _{0},i>j,ggT(i-j,1+i+j)=1$ haben (zur Hypotenuse) stets eine unkürzbare Höhe

$h={\frac {2(1+2i)(1+2j)}{{\frac {i-j}{1+i+j}}+{\frac {1+i+j}{i-j}}}}$ .

Verallgemeinerung auf pythagoreische (N + 1)-Tupel

Pythagoreische Tripel können als Punkte mit ganzzahligen Koordinaten auf einem Kreis mit ganzzahligem Radius aufgefasst werden. Diese Idee lässt sich auf beliebig viele Dimensionen verallgemeinern derart, dass ein pythagoreisches $(N+1)$ -Tupel einen Punkt mit ganzzahligen Koordinaten auf einer -dimensionalen Hypersphäre mit ganzzahligem Radius darstellt.

Alle diese $(N+1)$ -Tupel sind Lösungen der diophantischen Gleichung $\textstyle \sum _{k=1}^{N}x_{k}^{2}=r^{2}$ , wobei den Radius bezeichnet. Für jedes N > 1 sind für alle -Tupel ganzer Zahlen unendlich viele Lösungen dieser Gleichung durch die folgende Identität gegeben:

$\forall (z_{1},z_{2},\dotsc ,z_{N})\in \mathbb {Z} ^{N}\exists (x_{1},x_{2},\dotsc ,x_{N})\in \mathbb {Z} ^{N}\colon \sum _{k=1}^{N}x_{k}^{2}=r^{2},r\in \mathbb {N}$

mit $x_{N}=z_{N}^{2}-\sum _{k=1}^{N-1}z_{k}^{2}$ sowie $x_{k}=2z_{N}z_{k}$ für alle $k<N$ .

Damit ergibt sich als Summe von Quadraten ganzer Zahlen und somit als natürliche Zahl zu $\textstyle r=\sum _{k=1}^{N}z_{k}^{2}$ . Der Beweis erfolgt direkt durch Einsetzen und Vereinfachen:

Beweis der Identität

${\begin{aligned}\sum _{k=1}^{N}x_{k}^{2}&=\sum _{k=1}^{N-1}(2z_{N}z_{k})^{2}+\left(z_{N}^{2}-\sum _{k=1}^{N-1}z_{k}^{2}\right)^{2}\\&=\sum _{k=1}^{N-1}(2z_{N}z_{k})^{2}+\sum _{k=1}^{N}z_{k}^{4}+\sum _{k\neq j}^{N-1}\sum _{j=1}^{N-1}z_{k}^{2}z_{j}^{2}-2\sum _{j=1}^{N-1}z_{N}^{2}z_{j}^{2}\\&=\sum _{k=1}^{N}z_{k}^{4}+\sum _{k\neq j}^{N-1}\sum _{j=1}^{N-1}z_{k}^{2}z_{j}^{2}+2\sum _{j=1}^{N-1}z_{N}^{2}z_{j}^{2}\\&=\left(z_{N}^{2}+\sum _{k=1}^{N-1}z_{k}^{2}\right)^{2}\\&=\left(\sum _{k=1}^{N}z_{k}^{2}\right)^{2}\quad \square \\\end{aligned}}$

Dies stimmt offensichtlich mit der rechten Seite der Gleichung überein, womit die Gültigkeit der Identität für alle $(N+1)$ -Tupel ganzer Zahlen gezeigt ist.

Alternativer Beweis

Eine bequemere Notation des Sachverhaltes und eine Formulierung als Satz ergibt sich durch Betrachtung der folgenden Abbildung:

Seien $z\in \mathbb {Z} ^{N}$ sowie $Q\in \mathbb {Z} ^{N\times N}$ mit $Q(z):=2z_{N}I_{N}-e_{N}\cdot z^{T}$ , wobei $z_{N}$ die -te Komponente von , $I_{N}$ die $N\times N$ -Einheitsmatrix und $e_{N}\cdot z^{T}$ das dyadische Produkt des -ten kanonischen Einheitsvektors mit dem Vektor bezeichnen. Dann gilt:

$\forall z\in \mathbb {Z} ^{N}\colon Q(z)\cdot z\in \{q\in \mathbb {Z^{N}} \mid \|q\|\in \mathbb {N} \}$

Anschaulich handelt es sich hierbei um eine Abbildung, die jeden Gitterpunkt eines kartesischen Gitters auf einen weiteren solchen Gitterpunkt – mit der Eigenschaft, ganzzahligen euklidischen Abstand zum Ursprung zu haben – abbildet.

Der Beweis erfolgt auch hier durch einfaches Ausrechnen:

${\begin{aligned}Q(z)\cdot z&=\left(2z_{N}I_{N}-e_{N}\cdot z^{T}\right)\cdot z\\&=\left(\left({\begin{smallmatrix}2z_{N}&0&0&\ldots &0\\0&2z_{N}&0&\ldots &0\\\vdots &\vdots &\vdots &\ddots &\vdots \\0&0&0&\ldots &2z_{N}\end{smallmatrix}}\right)-\left({\begin{smallmatrix}0&0&0&\ldots &0\\0&0&0&\ldots &0\\\vdots &\vdots &\vdots &\ddots &\vdots \\z_{1}&z_{2}&z_{3}&\ldots &z_{N}\end{smallmatrix}}\right)\right)\cdot z\\&=\left({\begin{smallmatrix}2z_{N}&0&0&\ldots &0\\0&2z_{N}&0&\ldots &0\\\vdots &\vdots &\vdots &\ddots &\vdots \\-z_{1}&-z_{2}&-z_{3}&\ldots &z_{N}\end{smallmatrix}}\right)\cdot z\\&=\left(2z_{N}z_{1},2z_{N}z_{2},\dotsc ,2z_{N}z_{N-1},z_{N}^{2}-z_{1}^{2}-z_{2}^{2}-\dotsb -z_{N-1}^{2}\right)\quad \square \end{aligned}}$

Das entspricht gerade der zuvor bewiesenen Identität.

Anzahl der Lösungen

Die Anzahl der Lösungen der diophantischen Gleichung $\textstyle \sum _{k=1}^{N}x_{k}^{2}=r^{2}$ hängt sowohl von als auch von ab. Für N=3 und N=4 kann die Anzahl der Lösungen für $r\leq 10$ der folgenden Tabelle entnommen werden. Dabei bezeichnet $R_{N}(r)$ die Anzahl der Lösungen in Dimensionen für den Abstand und $Z_{N}(r)$ die Gesamtanzahl aller Lösungen mit Abstand $\leq r$ , es gilt also: $\textstyle Z_{N}(r)=\sum _{k=1}^{r}R_{N}(k)$

	1	02	003	004	005	006	0007	0008	0009	0010	Folge in der OEIS
$R_{3}(r)$	6	06	030	006	030	030	0054	0006	0102	0030	OEIS:A267651
$R_{4}(r)$	8	24	104	024	248	312	0456	0024	0968	0744	OEIS:A267326
$Z_{3}(r)$	6	12	042	048	078	108	0162	0168	0270	0300	OEIS:A267309
$Z_{4}(r)$	8	32	136	160	408	720	1176	1200	2168	2912	OEIS:A264390

Die Einträge in der Folge $R_{N}(r)$ sind durch $2N$ teilbar. Danny Rorabaugh hat dies am Beispiel $R_{3}(r)$ gezeigt.[Folge A267651 in OEIS] Der Beweis lässt sich problemlos auf alle verallgemeinern.

Gilt $R_{N}(r)=2N$ , so besitzt die diophantische Gleichung $\textstyle \sum _{k=1}^{N}x_{k}^{2}=r^{2}$ nur triviale Lösungen der Form $\textstyle \sum _{k=1}^{N-1}0^{2}+r^{2}=r^{2}$ . Interessanterweise muss $N\geq 4$ gelten, damit für alle r>1 eine nichttriviale Lösung existiert. Dies folgt unmittelbar aus dem Vier-Quadrate-Satz von Lagrange, wonach jede natürliche Zahl (und damit auch jede Quadratzahl) als Summe von höchstens vier Quadratzahlen darstellbar ist, und der Tatsache, dass die einzige Darstellung $2^{2}$ als Summe von Quadratzahlen durch $2^{2}=1^{2}+1^{2}+1^{2}+1^{2}$ gegeben ist.

Spezielle Tripel

(3,4,5) ist das kleinste Beispiel eines Pythagoreischen Tripels (x, x+1, z), bei dem sich die Katheten um 1 unterscheiden. Weitere pythagoreische Zwillingstripel sind (20, 21, 29), (119, 120, 169) und die mit x=696, 4059, 23660, 137903, 803760 beginnenden Tripel Schon A. Girard waren im 17. Jahrhundert 14 solcher Tripel bekannt, das höchste mit x=31509019100. Es gibt unendlich viele solcher Tripel, wie Pierre de Fermat zeigte, denn mit (x,x+1, z) ist auch (X, X+1, Z) mit X=2z+3x+1 ein solches Tripel. Eine weitere Formel ergibt sich aus der Standardform $(m^{2}-n^{2},2mn,m^{2}+n^{2})$ über $m^{2}-n^{2}=2mn\pm 1$ und Einsetzen von $m=x+y$ , $n=y$ als Lösung der Pell-Gleichung $x^{2}-2y^{2}=1$ . Es gibt noch weitere Bestimmungsmethoden. Sind m, n die Generatoren eines solchen Tripels in der oben angegebenen Standardform, so sind (2m+n, m) Generatoren eines weiteren Tripels. Aufeinanderfolgenden Werte $m_{r},n_{r}$ erhält man über $n_{r}=2n_{r-1}+n_{r-2}$ und es gilt $m_{r}=n_{r+1}$ . Werden die Katheterlängen $x_{r}$ der Lösungen nach Größe geordnet, so ist $x_{r}=6x_{r-1}-x_{r-2}+2$ und $z_{r}=6z_{r-1}+z_{r-2}$ . Es gibt auch explizite Formeln für $x_{r},z_{r}$ . Außerdem gibt es unendlich viele Zwillingstripel, bei denen sich eine Seite und die Hypotenuse um 1 unterscheidet wie (3,4,5), (7, 24, 25),(9, 40, 41), (11, 60, 61), (13, 84, 85), (15, 112, 113).

Zusammenhang mit den heronischen Dreiecken

Jedes zu einem pythagoreischen Tripel gehörige Dreieck ist ein heronisches Dreieck, das heißt, sowohl die Seitenlängen als auch der Flächeninhalt sind rationale Zahlen. Jedes heronische Dreieck lässt sich in zwei rechtwinklige Dreiecke zerlegen, die durch pythagoreische Tripel aus rationalen Zahlen gegeben sind.

Die Fermatsche Gleichung

Eine Verallgemeinerung der pythagoreischen Tripel erhält man, wenn man den Exponenten 2 durch eine natürliche Zahl ersetzt. Man untersucht also die diophantische Gleichung

$a^{n}+b^{n}=c^{n}\qquad (2<n\in \mathbb {N} )$

und sucht nach Lösungen durch ganze Zahlen $a,\ b,\ c$ unter Ausschluss der trivialen Lösungen, bei denen eine der drei Zahlen gleich Null ist, oder durch natürliche Zahlen.

Pierre de Fermat stellte um das Jahr 1637 die Behauptung auf, dass es keine derartigen Tripel gibt. Obwohl er keinen Beweis angab, wird diese Vermutung als großer Fermatscher Satz bezeichnet. Jahrhundertelang konnte kein Beweis gefunden werden. Die Suche danach führte aber zu vielen interessanten Erkenntnissen, insbesondere in der Zahlentheorie. Erst 1995 konnte der Mathematiker Andrew Wiles den Satz von Fermat schließlich beweisen.

Fermat besaß einen Beweis für den Fall n=4 und behandelte den eng verwandten Fall eines heronischen Dreiecks, dessen Flächeninhalt ein Quadrat ist (siehe Unendlicher Abstieg). Dieses Problem geht auch auf Diophant zurück.

Algorithmus

Ein möglicher Algorithmus in der Programmiersprache Haskell könnte folgendermaßen aussehen. Er erstellt für eine natürliche Zahl alle möglichen Tripel, deren Hypotenuse nicht überschreitet:

pythTripels n = [(k*x, k*y, k*z) | (x,y,z) <- primitives, k <- [1..n`div`z]] where
   primitives = [(p^2-q^2, 2*p*q, p^2+q^2) | p <- takeWhile (\p -> p^2+1 <= n) [1..], q <- takeWhile (\q -> p^2+q^2 <= n) [1..p], odd (p+q) && gcd p q == 1]

In Python ist List Comprehension ein elegantes Mittel, um pythagoreische Tripel zu bestimmen (Beispiel für alle Tripel mit c<100):

[(a, b, c) for a in range(1, 100) for b in range(a, 100) for c in range(b, 100) if a ** 2 + b ** 2 == c ** 2]

Literatur

Peter Bundschuh: Einführung in die Zahlentheorie. 6., überarbeitete und aktualisierte Auflage. Springer-Verlag, Berlin u.a. 2008, ISBN 978-3-540-76490-8.
Andreas Loos, Hans-Joachim Rein: Dreiecke mit ganzzahligen Seitenlängen und einem Innenwinkel von 60°, 90° oder 120°. In: Der mathematische und naturwissenschaftliche Unterricht (MNU). 37. Jahrg., 1984, Heft 5, S. 275–279.
Harald Scheid: Zahlentheorie. 3. Auflage. Spektrum Akademischer Verlag, Heidelberg u.a. 2003, ISBN 3-8274-1365-6.

Basierend auf einem Artikel in:

Wikipedia.de

m	n	a	b	c	m	n	a	b	c
2	1	3	4	5	7	2	45	28	53
4	1	15	8	17	5	4	9	40	41
3	2	5	12	13	10	1	99	20	101
6	1	35	12	37	9	2	77	36	85
5	2	21	20	29	8	3	55	48	73
4	3	7	24	25	7	4	33	56	65
8	1	63	16	65	6	5	11	60	61

a	b	c	a	b	c	a	b	c
3	4	5	11	60	61	19	180	181
4	3	5	12	35	37	20	99	101
5	12	13	13	84	85	21	220	221
*6	8	10	*14	48	50	*22	120	122
7	24	25	15	112	113	23	264	265
8	15	17	16	63	65	24	143	145
9	40	41	17	144	145	25	312	313
*10	24	26	*18	80	82	*26	168	170

m	n	a	b	c	m	n	a	b	c
2	1	3	4	5	7	2	45	28	53
4	1	15	8	17	5	4	9	40	41
3	2	5	12	13	10	1	99	20	101
6	1	35	12	37	9	2	77	36	85
5	2	21	20	29	8	3	55	48	73
4	3	7	24	25	7	4	33	56	65
8	1	63	16	65	6	5	11	60	61

a	b	c	a	b	c	a	b	c
3	4	5	11	60	61	19	180	181
4	3	5	12	35	37	20	99	101
5	12	13	13	84	85	21	220	221
*6	8	10	*14	48	50	*22	120	122
7	24	25	15	112	113	23	264	265
8	15	17	16	63	65	24	143	145
9	40	41	17	144	145	25	312	313
*10	24	26	*18	80	82	*26	168	170

m	n	a	b	c	m	n	a	b	c
2	1	3	4	5	7	2	45	28	53
4	1	15	8	17	5	4	9	40	41
3	2	5	12	13	10	1	99	20	101
6	1	35	12	37	9	2	77	36	85
5	2	21	20	29	8	3	55	48	73
4	3	7	24	25	7	4	33	56	65
8	1	63	16	65	6	5	11	60	61

a	b	c	a	b	c	a	b	c
3	4	5	11	60	61	19	180	181
4	3	5	12	35	37	20	99	101
5	12	13	13	84	85	21	220	221
*6	8	10	*14	48	50	*22	120	122
7	24	25	15	112	113	23	264	265
8	15	17	16	63	65	24	143	145
9	40	41	17	144	145	25	312	313
*10	24	26	*18	80	82	*26	168	170