Gaußsche Zahl

Gaußsche Zahlen als Gitterpunkte in der komplexen Zahlenebene

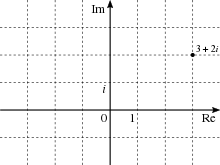
Die gaußschen Zahlen (nach Carl Friedrich Gauß; englisch Gaussian integer) sind eine Verallgemeinerung der ganzen Zahlen in den komplexen Zahlen. Jede gaußsche Zahl liegt auf einem ganzzahligen Koordinatenpunkt der komplexen Ebene. Die gaußschen Zahlen bilden den Ganzheitsring des quadratischen Zahlkörpers ${\mathbb {Q}}({\mathrm {i}})$ . Außerdem bilden die gaußschen Zahlen einen euklidischen Ring und damit insbesondere einen faktoriellen Ring.

Eine etwas kompliziertere Verallgemeinerung ganzer Zahlen, die ebenfalls in die komplexe Ebene eingebettet werden können, sind die Eisenstein-Zahlen.

Geschichtlicher Hintergrund

Gaußsche Zahlen wurden von Gauß in der Abhandlung Theorie der biquadratischen Reste. Zweite Abhandlung (1832, in Latein) erstmals eingeführt.

Das quadratische Reziprozitätsgesetz (das Gauß 1796 zum ersten Mal beweisen konnte) verknüpft die Lösbarkeit der Kongruenz $x^{2}\equiv q{\pmod {p}}$ mit der Lösbarkeit von $x^{2}\equiv p{\pmod {q}}$ . Ebenso verknüpft das kubische Reziprozitätsgesetz die Lösbarkeit der Kongruenz $x^{3}\equiv q{\pmod {p}}$ mit der von $x^{3}\equiv p{\pmod {q}}$ und das biquadratische Reziprozitätsgesetz ist die Verknüpfung von $x^{4}\equiv q{\pmod {p}}$ mit $x^{4}\equiv p{\pmod {q}}$ .

Gauß fand heraus, dass sich das biquadratische Reziprozitätsgesetz und die Ergänzungen dazu wesentlich einfacher als Aussagen über „ganze komplexe Zahlen“ (d.h. gaußsche Zahlen) formulieren und beweisen lassen.

In einer Fußnote (S. 541) erwähnt er, dass die Eisenstein-Zahlen der naturgemäße Bereich für Theoreme über kubische Reziprozität sind und ähnliche Erweiterungen der ganzen Zahlen die geeigneten Bereiche zur Untersuchung von höheren Potenzen.

Diese Abhandlung enthält nicht nur die Einführung gaußscher Zahlen, sondern auch der Begriffe Norm, Einheit, primär und Assoziierte, die heute in der algebraischen Zahlentheorie Standard sind.

Siehe dazu auch die Festschrift zum Zahlbericht.

Definition

Eine gaußsche Zahl ist durch

$g=a+b{\mathrm {i} }$

gegeben, wobei und ganze Zahlen sind.

Der Ring der gaußschen Zahlen heißt auch Gaußscher Zahlring und wird mit ${\mathbb Z}[{\mathrm i}]$ bezeichnet. Er entsteht also aus $\mathbb {Z}$ durch Adjunktion der imaginären Einheit $\mathrm {i}$ .

Die gaußschen Zahlen sind die Punkte mit ganzzahligen Koordinaten in der gaußschen Zahlenebene. Sie bilden ein zweidimensionales Gitter.

Primelemente

Das Spektrum von $\mathbb{Z}[\mathrm{i}]$ veranschaulicht diese Zusammenhänge: Die Kleckse entsprechen den Primelementen im Ring der gaußschen Zahlen, die in der Faktorisierung der jeweils unten angegebenen Primzahl auftauchen.

Primelemente in der komplexen Ebene. Durch Multiplikation mit den Einheiten entsteht die Rotationssymmetrie um 90°. Weil mit $a+\mathrm {i} b$ auch $\pm (b+\mathrm {i} a)$ Primelemente sind, liegen die Primelemente zusätzlich symmetrisch zu den Winkelhalbierenden $a=\pm b$ zwischen der reellen und der imaginären Achse.

Wie in jedem Ring kann man – analog zu $\mathbb {Z}$ – auch in $\mathbb{Z}[\mathrm{i}]$ Zahlentheorie betreiben. Insbesondere lassen sich Primelemente als Verallgemeinerung des Begriffes Primzahl definieren. Die Eindeutigkeit der Primfaktordarstellung gilt dann auch für die gaußschen Zahlen. Die Primelemente im Ring der Gaußschen Zahlen $\mathbb{Z } [{\mathrm i}]$ sind bis auf die Einheitsfaktoren $\pm 1,\pm \mathrm {i}$ genau die Primzahlen der Form $4k+3,\ k\in \mathbb {N} _{0}$ , das Element 1+i und die Elemente $a+b\cdot \mathrm {i} ,\ a,b\in \mathbb {Z}$ , für die $a^{2}+b^{2}=p$ eine Primzahl ist, die man als $p=4k+1,\ k\in \mathbb {Z}$ schreiben kann.

Die Primelemente im Ring der gaußschen Zahlen haben einen engen Bezug zu den gewöhnlichen Primzahlen. Sie zerfallen in drei Klassen (jeweils bis auf Assoziiertheit, d.h. bis auf Multiplikation mit $\pm 1$ und $\pm \mathrm {i}$ , den Einheiten des Ringes der gaußschen Zahlen):

Der doppelte Primfaktor von 2:

Die Zahl 2 kann als Produkt der Primelemente $1+{\mathrm i}$ und $1-\mathrm {i}$ geschrieben werden, die sich aber wegen $1+\mathrm {i} =\mathrm {i} \cdot (1-\mathrm {i} )$ nur um eine Einheit unterscheiden. Also gilt $(1+\mathrm {i} )(1-\mathrm {i} )=\mathrm {i} ^{3}\cdot (1+\mathrm {i} )^{2}$ und die – bis auf Assoziiertheit der Faktoren eindeutige – Primfaktorzerlegung

$2=\mathrm {i} ^{3}\cdot (1+\mathrm {i} )^{2}$

zeigt, dass 2 zum Quadrat des Primelements $1+{\mathrm i}$ assoziiert ist (2 ist verzweigt).

Faktoren von Primzahlen der Form 4k + 1:

Ist eine Primzahl der Form 4k+1 mit einer natürlichen Zahl , so lässt sich auf im Wesentlichen eindeutige Weise als Summe zweier Quadratzahlen schreiben (siehe Zwei-Quadrate-Satz):

$p=a^{2}+b^{2}$ mit gewissen $a,b\in \mathbb {Z}$

Dann ist

$p=(a+b{\mathrm i})(a-b{\mathrm i})$

die Primfaktorzerlegung von , selbst ist also kein Primelement im Ring der gaußschen Zahlen, sondern Produkt zweier konjugierter Primelemente ( ist zerlegt). Beispielsweise ist $5=(2+\mathrm {i} )(2-\mathrm {i} )$ kein Primelement, aber $2+\mathrm {i}$ und $2-\mathrm {i}$ sind zwei Primelemente.

Primzahlen der Form 4k + 3:

Ist eine Primzahl der Form $4k+3$ mit einer natürlichen Zahl , so ist auch im Ring der gaußschen Zahlen ein Primelement ( bleibt prim, es ist träge).

Die drei Fälle beschreiben das Verhalten von Primelementen bei Erweiterung des Körpers der rationalen Zahlen zum Körper der Gaußschen Zahlen (entstanden durch Adjunktion der imaginären Einheit).

Primfaktorzerlegung

Eine bis auf die Reihenfolge der Faktoren eindeutige Primfaktorzerlegung für eine beliebige gaußsche Zahl $z\neq 0$ ergibt sich z.B., wenn man $p_{1}=1+\mathrm {i}$ setzt und von den vier Assoziierten jedes ungeraden Primelements $p_{m}$ das durch die Forderung $p_{m}\equiv 1{\pmod {2+2\mathrm {i} }}$ (s.w.u. Kongruenzen und Restklassen) eindeutig bestimmte sog. primäre auswählt und diese nach ihrer Norm sortiert:

${\begin{aligned}&p_{2}=-1+2\mathrm {i} ,\quad p_{3}=-1-2\mathrm {i} ,\quad p_{4}=-3,\quad p_{5}=+3+2\mathrm {i} ,\quad \\&p_{6}=+3-2\mathrm {i} ,\quad p_{7}=+1+4\mathrm {i} ,\quad p_{8}=+1-4\mathrm {i} ,\;\dots ,\;p_{15}=-7,\dotsc \end{aligned}}$

(offensichtlich sind hierbei die natürlichen Primzahlen der Form $4k+3$ immer mit negativem Vorzeichen zu versehen, da $4k+3\equiv 3\equiv -1{\pmod {2+2\mathrm {i} }}$ ). Die obige Definition erfüllt offensichtlich ein wichtiges Kriterium: Das Produkt beliebiger primärer Gaußscher Zahlen ist ebenfalls eine primäre Zahl. Damit erhält man

$z={\mathrm {i} }^{k}\prod _{m\in \mathbb {N} }p_{m}^{\nu _{m}}$ mit $k=0,\dotsc ,3$ und $\nu _{m}\geq 0$ (darin gilt natürlich nur für endlich viele Exponenten $\nu _{m}>0$ ).

Eine andere, häufig benutzte Primfaktordarstellung ergibt sich, wenn man darin die überflüssigen Faktoren $p_{k}^{0}=1$ weglässt, und nur die Primteiler von berücksichtigt, d.h. alle $p_{m}$ mit $\nu _{m}>0$ . Dies seien die Zahlen $q_{n}\in \{p_{1},\dots \},\;n=1,\dots ,r$ . Damit lautet die Darstellung

$z={\mathrm {i} }^{k}\prod _{n=1}^{r}q_{n}^{\mu _{n}}$ mit $k=0,\dotsc ,3$ und $\mu _{n}>0$

Euklidischer Algorithmus und größter gemeinsamer Teiler (ggT)

Jede gaußsche Zahl $g\neq 0$ hat vier Assoziierte $\pm g,\pm \mathrm {i} g$ , die durch Multiplikation mit den Einheiten gebildet werden und in allen vier Quadranten der komplexen Zahlenebene liegen.
Ein größter gemeinsamer Teiler (ggT) zweier gaußscher Zahlen a,b ist definiert als gaußsche Zahl mit folgenden zwei Eigenschaften:

$t\mid a$ und $t\mid b,\,$ d.h.: ist ein gemeinsamer Teiler von und .
Aus $s\mid a$ und $s\mid b$ folgt $s\mid t,\,$ d.h.: Jeder gemeinsame Teiler von und teilt auch .

Daraus folgt: Alle gaußschen Zahlen mit diesen Eigenschaften (bei gegebenem a,b ) sind assoziiert. Der ggT ist somit eine im Wesentlichen (bis auf Assoziierte) eindeutig bestimmte gaußsche Zahl mit der üblichen Schreibweise $t=(a,b)$ .

Sofern die Primfaktorzerlegung von und bekannt ist, also $a=i^{k}\prod _{m}p_{m}^{\nu _{m}},\,b=i^{n}\prod _{m}p_{m}^{\mu _{m}}$ , ist der ggT natürlich sofort gegeben durch $(a,b)=\prod _{m}p_{m}^{\lambda _{m}}$ mit $\lambda _{m}=\mathrm {min} (\nu _{m},\mu _{m})$ .

Veranschaulichung des Euklidischen Algorithmus

Andernfalls kann man den euklidischen Algorithmus benutzen: Zur Bestimmung des ggT zweier Zahlen $z_{0},z_{1}$ läuft er ähnlich ab wie für ganze Zahlen. Es gilt $(z_{0},0)=z_{0}$ für alle $z_{0}$ (also insbesondere $(0,0)=0$ ). Und für $z_{1}\neq 0$ gibt es ein Paar gaußscher Zahlen $q_{1},z_{2}$ mit

$z_{0}=q_{1}z_{1}+z_{2}$ und $|z_{2}|<|z_{1}|.$

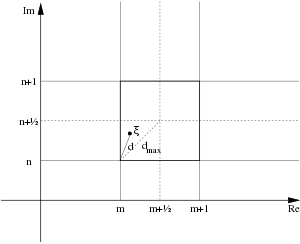
Man bestimmt dazu $q_{1}=m+n\mathrm {i}$ als diejenige gaußsche Zahl, die dem Bruch $\xi :={\frac {z_{0}}{z_{1}}}$ am nächsten liegt. Dafür gilt stets $\left|m-\operatorname {Re} (\xi )\right|\leq {\frac {1}{2}}$ und $\left|n-\operatorname {Im} (\xi )\right|\leq {\frac {1}{2}}$ , also $d:=\left|q_{1}-\xi \right|\leq d_{\text{max}}={\frac {1}{\sqrt {2}}}$ und folglich $|z_{2}|\leq {\frac {|z_{1}|}{\sqrt {2}}}$ .

Falls $z_2 \neq 0$ , wird das fortgesetzt mit $z_{1}=q_{2}z_{2}+z_{3}$ und $|z_{3}|<|z_{2}|$ usw. bis $z_{n+1}=0$ . Dann ist $z_{{n}}$ der gesuchte ggT: $(z_{0},z_{1})=z_{n}$ .

Beispiel:
Gesucht sei der ggT der gaußschen Zahlen $z_{0}=5+\mathrm {i} ,\;z_{1}=2$ . Der Quotient ist ${\frac {z_{0}}{z_{1}}}=2{,}5+0{,}5\mathrm {i}$ . Für $q_{1}$ kommen damit die vier gaußschen Zahlen $2,2+\mathrm {i} ,3,3+\mathrm {i}$ in Frage. Wir wählen z.B. $q_{1}=2$ und erhalten $z_{2}=z_{0}-q_{1}z_{1}=5+\mathrm {i} -4=1+\mathrm {i}$ . Der nächste Schritt ergibt ${\frac {z_{1}}{z_{2}}}={\frac {2}{1+\mathrm {i} }}=1-\mathrm {i}$ , d.h., der Rest ist $z_{3}=0$ : Der Algorithmus bricht ab und wir erhalten als ggT ${\underline {(5+\mathrm {i} ,2)=z_{2}=1+\mathrm {i} }}$ .

Kongruenzen und Restklassen

Zwei gaußsche Zahlen $z_{1},z_{2}$ heißen kongruent bezüglich eines gaußschen Moduls $z_{0}$ , wenn es eine gaußsche Zahl gibt mit $z_{1}-z_{2}=qz_{0}$ . Man schreibt dafür $z_{1}\equiv z_{2}{\pmod {z_{0}}}$ . Dann gibt es auch einen gemeinsamen Rest mit $z_{1}=q_{1}z_{0}+r,\,z_{2}=q_{2}z_{0}+r$ . Wie oben kann man die Faktoren $q_{1},q_{2}$ so bestimmen, dass $|r|\leq {\frac {|z_{0}|}{\sqrt {2}}}$ gilt.

Die Kongruenzrelation $R_{z_{0}}$ nach dem Modul $z_{0}$ induziert im Gaußschen Zahlring ${\mathbb Z}[{\mathrm i}]$ eine Klasseneinteilung $\mathbb {Z} [\mathrm {i} ]/R_{z_{0}}$ . Man definiert ${\bar {a}}$ als die Menge aller gaußschen Zahlen , für die gilt: $z\equiv a{\pmod {z_{0}}}$ . Die Menge ${\bar {a}}$ nennt man eine Restklasse modulo $z_{0}$ . Damit gilt:

${\bar {a}}={\bar {b}}$ genau dann, wenn $a\equiv b{\pmod {z_{0}}}$

Addition und Multiplikation von Kongruenzen sind sehr einfach: Aus $a_{1}\equiv b_{1}{\pmod {z_{0}}}$ und $a_{2}\equiv b_{2}{\pmod {z_{0}}}$ folgt:

$a_{1}+a_{2}\equiv b_{1}+b_{2}{\pmod {z_{0}}}$

$a_{1}\cdot a_{2}\equiv b_{1}\cdot b_{2}{\pmod {z_{0}}}$

Das zeigt, dass die Definitionen

${\bar {a}}+{\bar {b}}:={\overline {a+b}}$

${\bar {a}}\cdot {\bar {b}}:={\overline {ab}}$

für die Summe und das Produkt von Restklassen wohldefiniert (d.h. repräsentantenunabhängig) und daher gerechtfertigt sind. Die Menge $\mathbb {Z} [\mathrm {i} ]/R_{z_{0}}$ der Restklassen bildet dann mit diesen Operationen einen kommutativen Ring mit ${\bar 0}$ als Nullelement und ${\bar {1}}$ als Einselement, den sogenannten Restklassenring modulo $z_{0}$ .

Beispiele:

Es gibt genau zwei Restklassen zum Modul $z_{0}=1+\mathrm {i}$ , nämlich das Hauptideal ${\bar {0}}=\{0,\pm 2,\pm 4,\dotsc ,\pm 1\pm \mathrm {i} ,\pm 3\pm \mathrm {i} ,\dotsc \}$ aller Vielfachen $z\cdot (1+\mathrm {i} )$ des Moduls und ${\bar {1}}=\{\pm 1,\pm 3,\dotsc ,\pm \mathrm {i} ,\pm 2\pm \mathrm {i} ,\dotsc \}$ , die ein Schachbrettmuster in der gaußschen Zahlenebene bilden. Sie können als Erweiterung der geraden bzw. ungeraden natürlichen Zahlen angesehen und deshalb als (un)gerade gaußsche Zahlen bezeichnet werden (Gauß unterteilt die geraden Zahlen noch in halbgerade und gerade, d.h. durch 2 teilbare).
Zum gaußschen Modul $z_{0}=2$ gibt es genau vier Restklassen, nämlich ${\bar {0}},{\bar {1}},{\bar {\mathrm {i} }},{\overline {1+\mathrm {i} }}$ . (Man beachte, dass z.B. $1+\mathrm {i} \equiv \pm 1\pm \mathrm {i} {\pmod {2}}$ gilt.)

Vollständige Restsysteme

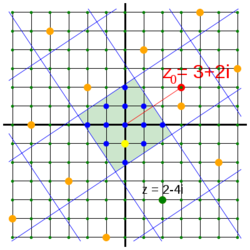
Alle 13 Restklassen mit ihren minimalen Resten (blaue Punkte) im Quadrat $Q_{00}$ (hellgrün markiert) zum Modul $z_{0}=3+2\mathrm {i}$ . Eine Restklasse mit $z=2-4\mathrm {i} \equiv {-i}{\pmod {z_{0}}}$ ist z.B. durch orange/gelbe Punkte hervorgehoben.

Um alle Restklassen zu einem Modul $z_{0}$ zu bestimmen, kann man mit der Abbildung $z(s,t)=(s+\mathrm {i} t)z_{0}$ ein quadratisches Gitter über die komplexe Zahlenebene legen. Die Gitterlinien seien die Geraden mit $s=\pm {\frac {1}{2}},\pm {\frac {3}{2}},\dotsc$ und $t \in \mathbb{R}$ bzw. $t=\pm {\frac {1}{2}},\pm {\frac {3}{2}},\dotsc ,s\in \mathbb {R}$ . Sie zerteilen die Ebene in Quadrate $Q_{mn}$ (mit ganzzahligen m,n ) $s=\left[m-{\frac {1}{2}},m+{\frac {1}{2}}\right),t=\left[n-{\frac {1}{2}},n+{\frac {1}{2}}\right)$ . Die vier Eckpunkte von $Q_{00}$ sind die assoziierten Punkte ${\frac {\pm 1\pm i}{2}}z_{0}$ . Wenn $z_{0}$ eine gerade gaußsche Zahl ist, sind alle vier gaußsche Zahlen (und auch kongruent zueinander), ansonsten keine. Im ersten Fall nehmen wir z.B. nur den Eckpunkt ${\frac {-1-\mathrm {i} }{2}}z_{0}$ als zu $Q_{00}$ gehörig. Innerhalb jedes Quadrates sind alle gaußschen Zahlen inkongruent, wenn man jeweils die oberen Grenzen ausschließt: $s<m+{\frac {1}{2}},t<n+{\frac {1}{2}}$ (wenn auf den Grenzlinien gaußsche Zahlen liegen, dann immer paarweise kongruente Zahlen).

Das Quadrat $Q_{00}$ beschreibt damit alle minimalen Reste, in dem Sinne, dass alle anderen Elemente in den Restklassen betragsmäßig nicht kleiner sind (Gauß bezeichnet sie als absolut kleinste Reste).

Daraus lässt sich mit einfachen geometrischen Überlegungen ableiten, dass die Anzahl der Restklassen zu einem gegebenen Modul $z_{0}=m+n\mathrm {i}$ gleich seiner Norm $N(z_{0}):=|z_{0}|^{2}=m^{2}+n^{2}$ ist (bei den natürlichen Zahlen ist die Anzahl der Restklassen zu einem Modul trivialerweise gleich dem Betrag |m| ).

Man sieht sofort, dass alle Quadrate deckungsgleich sind (inklusive der Gitterpunkte). Sie haben die Seitenlänge $|z_{0}|$ , also die Fläche $F=|z_{0}|^{2}=m^{2}+n^{2}$ und in allen liegt die gleiche Anzahl gaußscher Zahlen, die wir mit $N_{g}$ bezeichnen. Allgemein ist die Zahl von Gitterpunkten in einem beliebigen Quadrat der Fläche bestimmt durch $A+O({\sqrt {A}})$ . Betrachten wir nun ein großes Quadrat aus $k\times k$ Quadraten $Q_{mn}$ , dann liegen darin folglich stets $k^{2}F+O(k{\sqrt {F}})$ Gitterpunkte. Es gilt also $k^{2}N_{g}=k^{2}F+O(k{\sqrt {F}})$ , was im Limes $k\to \infty$ ${\underline {N_{g}=F=m^{2}+n^{2}}}$ ergibt.

Prime Restklassengruppe und eulersche Phi-Funktion

Viele Sätze (und Beweise) für Moduln ganzer Zahlen lassen sich direkt auf Moduln gaußscher Zahlen übertragen, indem man jeweils den Betrag des Moduls durch die Norm ersetzt. Insbesondere gilt das für die prime Restklassengruppe und den Satz von Fermat-Euler, wie hier kurz ergänzt werden soll.

Die prime Restklassengruppe (pRG) des Restklassenringes modulo ist die multiplikative Gruppe seiner Einheiten. Sie besteht aus allen Restklassen ${\bar {a}}$ mit zu teilerfremdem , für die also gilt: $(a,z)=1$ . Die Anzahl ihrer Elemente sei bezeichnet als $\phi (z)$ (analog zur eulerschen Phi-Funktion $\varphi (m)$ für ganze Zahlen ). Für Primelemente ergibt sich sofort $\phi (p)=|p|^{2}-1$ und für beliebige (zusammengesetzte) gaußsche Zahlen kann man die eulersche Produktformel

$\phi (z)=|z|^{2}\prod _{p_{m}|z}\left(1-{\frac {1}{|p_{m}|^{2}}}\right)$

ableiten, wobei das Produkt über alle Primteiler von $z=\mathrm {i} ^{k}\prod _{m}p_{m}^{\nu _{m}}$ (mit $\nu _{m}>0$ ) zu erstrecken ist.

Auch der wichtige Satz von Fermat-Euler ist sofort übertragbar:

Aus $(a,z)=1$ folgt $a^{\phi (z)}\equiv 1{\pmod {z}}$ .

Mit Hilfe dieses Satzes kann man z.B. einige diophantische Gleichungen für gaußsche Zahlen explizit lösen. Beispielsweise seien x,y als Lösungen der linearen Gleichung

$ax+by=c$

für gegebene gaußsche Zahlen a,b,c gesucht. Dafür kann man o.B.d.A. $(a,b)=1$ annehmen, da jeder gemeinsame Teiler von und auch ein Teiler von sein muss (andernfalls hat die Gleichung keine Lösung) und deshalb herausgekürzt werden kann.

Dazu betrachtet man diese Gleichung modulo , was ergibt $ax\equiv c{\pmod {b}}$ . Der Satz von Fermat-Euler liefert dann eine explizite Lösung , nämlich

$x\equiv ca^{\phi (b)-1}{\pmod {b}}$ ,

d.h. alle gaußsche Zahlen der Form $x=ca^{\phi (b)-1}+ub$ mit beliebigen gaußschen Faktoren . Eingesetzt in die Ausgangsgleichung ergibt das

$y=c{\frac {1-a^{\phi (b)}}{b}}-ua$ ,

was nach dem Satz von Fermat-Euler ebenfalls eine gaußsche Zahl ist.

Ungelöste Probleme

Die Verteilung der gaußschen Primzahlen in der Ebene

Die meisten der ungelösten Probleme haben mit der Verteilung der gaußschen Primzahlen in der Ebene zu tun.

Das Gaußsche Kreisproblem (engl. Gauss's circle problem) beschäftigt sich nicht mit gaußschen Zahlen an sich, sondern fragt nach der Anzahl der Gitterpunkte innerhalb eines Kreises mit gegebenem Radius um den Koordinatenursprung. Das ist äquivalent der Bestimmung der Anzahl gaußscher Zahlen mit der Norm kleiner als ein gegebener Wert.

Zwei ungelöste Probleme über gaußsche Primzahlen sind z.B.

Auf den reellen und imaginären Koordinatenlinien liegen unendlich viele gaußsche Primzahlen 3, 7, 11, 19, … und deren Assoziierte. Gibt es weitere Geraden, auf denen unendlich viele Primzahlen liegen? Insbesondere: Gibt es unendlich viele Primzahlen der Form $1+k\mathrm {i}$ ?

Ist es möglich, durch die Ebene der gaußschen Zahlen bis ins Unendliche zu wandern, indem man die gaußschen Primzahlen als Stützstellen benutzt und dabei nur Schritte begrenzter Länge macht? Das ist als Gaußsches Grabenproblem (engl. Gaussian moat problem) bekannt; es wurde 1962 aufgestellt von Basil Gordon und ist noch ungelöst.

Literatur

Peter Bundschuh: Einführung in die Zahlentheorie. 6., überarbeitete und aktualisierte Auflage. Springer-Verlag, Berlin u.a. 2008, ISBN 978-3-540-76490-8.
Harald Scheid: Zahlentheorie. 3. Auflage. Spektrum Akademischer Verlag, Heidelberg u.a. 2003, ISBN 3-8274-1365-6.

Basierend auf einem Artikel in:

Wikipedia.de