Konfidenzintervall

Konfidenzintervalle zum Niveau 95 % für 100 Stichproben vom Umfang 30 aus einer normalverteilten Grundgesamtheit. Davon überdecken 94 Intervalle den exakten Erwartungswert μ = 5; die übrigen 6 tun das nicht.

Ein Konfidenzintervall, kurz KI, (auch Vertrauensintervall, Vertrauensbereich oder Erwartungsbereich genannt) ist in der Statistik ein Intervall, das die Präzision der Lageschätzung eines Parameters (z.B. eines Mittelwerts) angeben soll. Das Konfidenzintervall gibt den Bereich an, der mit einer gewissen Wahrscheinlichkeit (der Überdeckungswahrscheinlichkeit) den Parameter einer Verteilung einer Zufallsvariablen einschließt. Ein häufig verwendetes Konfidenzniveau ist 95 %.

Die häufig anzutreffende Formulierung, dass der wahre Wert mit 95 % Wahrscheinlichkeit im für die vorliegende Stichprobe berechneten Konfidenzintervall liegt, ist streng genommen nicht korrekt, da der wahre Wert keine Zufallsgröße, nicht stochastisch ist. Stochastisch sind vielmehr die obere und untere Grenze des Konfidenzintervalls. Folglich lautet die korrekte Formulierung: Bei der Berechnung eines Konfidenzintervalls mit einem bestimmten Schätzverfahren enthält es den wahren Wert mit 95 % Wahrscheinlichkeit. Es handelt sich nicht um eine Eigenschaft des Intervalls, sondern des Verfahrens. Wird es für viele Stichproben aus derselben Grundgesamtheit wiederholt, so sollte es Konfidenzintervalle liefern, die den wahren Wert $\beta_j$ näherungsweise mit einer dem Konfidenzniveau $1-\alpha$ entsprechenden relativen Häufigkeit überdecken.

Das Schätzen von Parametern mit Hilfe von Konfidenzintervallen wird Intervallschätzung genannt, die entsprechende Schätzfunktion ein Bereichs- oder Intervallschätzer. Ein Vorteil gegenüber Punktschätzern ist, dass man an einem Konfidenzintervall direkt die Signifikanz ablesen kann: ein für ein vorgegebenes Konfidenzniveau breites Intervall weist auf einen geringen Stichprobenumfang oder auf eine starke Variabilität in der Grundgesamtheit hin.

Abzugrenzen von Konfidenzintervallen sind Prognoseintervalle sowie Konfidenz- und Vorhersagebänder.

Definition

Für ein fest vorgegebenes $\gamma \in (0,1)$ ist ein $\gamma \cdot 100\,\%$ -Konfidenzintervall für $\vartheta$ zum Konfidenzniveau $\gamma$ (auch: ein $\gamma$ -Konfidenzintervall) durch die beiden – auf einer Zufallsstichprobe $X_{1:n}$ basierenden – Statistiken $T_{u}=h_{u}(X_{1:n})$ und $T_{v}=h_{v}(X_{1:n})$ definiert, welche

$P\left(T_{u}\leq \vartheta \leq T_{v}\right)=\gamma \quad \mathrm {f{\ddot {u}}r\;alle\;} \vartheta \in \Theta$

erfüllen. Die Statistiken $T_{u}$ und $T_{v}$ sind die Grenzen des Konfidenzintervalls, für die stets $T_{u}<T_{v}$ angenommen wird. Das Konfidenzniveau $\gamma$ wird auch Überdeckungswahrscheinlichkeit genannt. Die Realisierungen $t_{u}$ und $t_{v}$ von $T_{u}$ bzw. $T_{v}$ bilden das Schätzintervall $[t_{u},t_{v}]$ . Die Grenzen des Konfidenzintervalls sind Funktionen der Zufallsstichprobe $X_{1:n}$ und daher ebenfalls zufällig. Im Gegensatz dazu ist der unbekannte Parameter $\vartheta$ fest. Wenn man das Zufallsexperiment auf identische Art und Weise wiederholt, dann wird ein $\gamma \cdot 100\,\%$ -Konfidenzintervall den unbekannten Parameter $\vartheta$ in $\gamma \cdot 100\,\%$ aller Fälle überdecken. Da der unbekannte Parameter $\vartheta$ keine Zufallsvariable ist, kann man allerdings nicht sagen, dass $\vartheta$ in einem $\gamma \cdot 100\,\%$ -Konfidenzintervall mit Wahrscheinlichkeit $\gamma$ liegt. Solch eine Interpretation ist dem bayesschen Pendant von Konfidenzintervall, den sogenannten Glaubwürdigkeitsintervallen vorbehalten. Das Konfidenzniveau $\gamma$ wird auch Überdeckungswahrscheinlichkeit genannt. Oft setzt man $\gamma =1-\alpha$ . Die Wahrscheinlichkeit $1-\alpha$ lässt sich als relative Häufigkeit interpretieren: Verwendet man für eine große Anzahl von Konfidenzschätzungen Intervalle, die jeweils das Niveau $1-\alpha$ besitzen, so nähert sich die relative Häufigkeit, mit denen die konkreten Intervalle den Parameter überdecken, dem Wert $1-\alpha$ .

Formale Definition

Rahmenbedingungen

Gegeben sei ein statistisches Modell $(X,{\mathcal A},(P_{\vartheta })_{{\vartheta \in \Theta }})$ sowie eine Funktion

$g\colon \Theta \to \Gamma$ ,

die im parametrischen Fall auch Parameterfunktion genannt wird. Die Menge $\Gamma$ enthält die Werte, die Ergebnis einer Schätzung sein können. Meist ist $\Gamma \subset \mathbb {R} ^{n}$

Konfidenzbereich

Eine Abbildung

$C\colon X\to {\mathcal {P}}(\Gamma )$

heißt ein Konfidenzbereich, Vertrauensbereich, Bereichsschätzfunktion oder ein Bereichsschätzer, wenn sie die folgende Bedingung erfüllt:

Für alle $\gamma \in \Gamma$ ist die Menge $A(\gamma ):=\{x\in X\mid \gamma \in C(x)\}$ in $\mathcal A$ enthalten. (M)

Ein Konfidenzbereich ist also eine Abbildung, die jeder Beobachtung $x\in X$ eine vorerst beliebige Teilmenge von $\Gamma$ zuordnet ( ${\mathcal {P}}(\Gamma )$ ist hier die Potenzmenge der Menge $\Gamma$ , also die Menge aller Teilmengen von $\Gamma$ )

Die Bedingung (M) stellt sicher, dass allen Mengen $A(\gamma )$ eine Wahrscheinlichkeit zugeordnet werden kann. Dies wird zur Definition des Konfidenzniveaus benötigt.

Konfidenzintervall

Ist $\Gamma \subset \mathbb {R}$ und ist $C(x)$ für jedes $x\in X$ immer ein Intervall, so heißt auch ein Konfidenzintervall.

Werden Konfidenzintervalle in der Form

$C_{1}(x)=(-\infty ,b^{+}(x)],\;C_{2}(x)=[b^{-}(x),b^{+}(x)]\;\;{\text{oder}}\;\;C_{3}(x)=[b^{-}(x),+\infty )$ ,

definiert, so nennt man $b^{+}(x)$ auch die obere Konfidenzschranke und $b^{-}(x)$ die untere Konfidenzschranke.

Konfidenzniveau und Irrtumsniveau

Gegeben sei ein Konfidenzbereich . Dann heißt ein Konfidenzbereich zum Konfidenzniveau oder Sicherheitsniveau $1-\alpha$ , wenn

$P_{\vartheta }(\{x\in X\mid g(\vartheta )\in C(x)\})\geq 1-\alpha \quad \mathrm {f{\ddot {u}}r\;alle\;} \vartheta \in \Theta$ .

Der Wert $\alpha$ wird dann auch das Irrtumsniveau genannt.

Für die oben genannten Spezialfälle bei Konfidenzbereichen mit oberer und unterer Konfidenzschranke ergibt sich somit

$P_{\vartheta }(g(\vartheta )\leq b^{+}(x))\geq 1-\alpha$

bzw.

$P_{\vartheta }(b^{-}(x)\leq g(\vartheta )\leq b^{+}(x))\geq 1-\alpha$

und

$P_{\vartheta }(b^{-}(x)\leq g(\vartheta ))\geq 1-\alpha \quad \mathrm {f{\ddot {u}}r\;alle\;} \vartheta \in \Theta .$

Konstruktion von Konfidenzintervallen

Konstruktion des Wald-Konfidenzintervalls

Wald-Konfidenzintervalle können mittels der sogenannten Wald-Statistik berechnet werden. Beispielsweise gilt für das asymptotische Wald-Konfidenzintervall, dass es mittels der Fisher-Information, der negativen zweiten Ableitung der Log-Likelihood-Funktion, konstruiert werden kann. So umschließen die Intervallgrenzen des folgenden Konfidenzintervalls in 95 % der Fälle den wahren Parameter $\theta$ (asymptotisch für große Stichprobenumfänge)

${\hat {\theta }}_{ML}\pm 1{,}96{\frac {1}{\sqrt {-{\frac {\partial ^{2}}{\partial \theta ^{2}}}\ell ({\hat {\theta }}_{ML})}}}$ ,

wobei $\ell (\cdot )=\log {\mathcal {L}}(\cdot )$ die Log-Likelihood-Funktion und $-{\frac {\partial ^{2}}{\partial \theta ^{2}}}\ell ({\hat {\theta }}_{ML})$ die beobachtete Fisher-Information darstellt (die Fisher-Information an der Stelle des ML-Schätzers ${\hat {\theta }}_{ML}$ ).

Der Ausdruck ${\frac {1}{\sqrt {-{\frac {\partial ^{2}}{\partial \theta ^{2}}}\ell ({\hat {\theta }}_{ML})}}}$ wird auch als Standardfehler des Maximum-Likelihood-Schätzers bezeichnet. Häufig wird statt der beobachteten Fisher-Information auch die erwartete Fisher-Information $\operatorname {E} \left(-{\frac {\partial ^{2}}{\partial \theta ^{2}}}\ell ({\hat {\theta }}_{ML})\right)$ verwendet.

Beispiel

Wird die Likelihood zum Beispiel mithilfe einer angenommenen Normalverteilung und einer Stichprobe (deren Variablen unabhängig und identisch verteilte Zufallsvariablen sind) mit Größe berechnet, so ist $-{\frac {\partial ^{2}}{\partial \mu ^{2}}}\ell ({\hat {\mu }},{\hat {\sigma }})=-\left({\frac {\partial ^{2}}{\partial \mu ^{2}}}\sum _{i=1}^{N}{\frac {-(x_{i}-\mu )^{2}}{2\sigma ^{2}}}\right)_{(\mu ={\hat {\mu }},\sigma ={\hat {\sigma }})}=\sum _{i=1}^{N}{\frac {1}{{\hat {\sigma }}^{2}}}={\frac {N}{{\hat {\sigma }}^{2}}}$ und somit

${\frac {1}{\sqrt {-{\frac {\partial ^{2}}{\partial \theta ^{2}}}\ell ({\hat {\theta }}_{ML})}}}={\frac {1}{\sqrt {\frac {N}{{\hat {\sigma }}^{2}}}}}={\frac {\hat {\sigma }}{\sqrt {N}}},$ also der bekannte Standardfehler des Mittelwertes.

Konstruktion anderer Konfidenzintervalle

Konfidenzintervalle lassen sich auch mithilfe von alternativen Parametrisierungen der Log-Likelihood-Funktion finden: zum Beispiel kann die Logit-Transformation oder der Logarithmus verwendet werden. Dies ist vorteilhaft, wenn die Log-Likelihood-Funktion sehr schief ist. Auch mithilfe des Likelihood-Quotienten können Konfidenzintervalle konstruiert werden.

Eine nichtparametrische Art Konfidenzintervalle zu schätzen sind Bootstrap-Konfidenzintervalle, bei denen man keine Verteilung annehmen muss, sondern Bootstrapping benutzt.

Beschreibung des Verfahrens

Man interessiert sich für den unbekannten Parameter $\vartheta$ einer Grundgesamtheit. Dieser wird durch eine Schätzfunktion aus einer Stichprobe vom Umfang geschätzt. Es wird davon ausgegangen, dass die Stichprobe eine einfache Zufallsstichprobe ist, in etwa die Grundgesamtheit widerspiegelt und dass deshalb die Schätzung in der Nähe des wahren Parameters liegen müsste. Die Schätzfunktion ist eine Zufallsvariable mit einer Verteilung, die den Parameter $\vartheta$ enthält.

Man kann zunächst mit Hilfe der Verteilung ein Intervall angeben, das den unbekannten wahren Parameter $\vartheta$ mit einer Wahrscheinlichkeit $\gamma =1-\alpha$ überdeckt. Ermitteln wir z.B. das 95-%-Konfidenzintervall für den wahren Erwartungswert $\mu$ einer Grundgesamtheit, dann bedeutet dies, dass wir ein Konfidenzintervall ermitteln, das bei durchschnittlich 95 von 100 gleich großen Zufallsstichproben den Erwartungswert enthält.

Beispiel

Das Verfahren kann anhand eines normalverteilten Merkmals mit dem unbekannten Erwartungswert $\mu$ und der bekannten Varianz $\sigma ^{2}$ demonstriert werden: Es soll der Erwartungswert $\mu$ dieser Normalverteilung geschätzt werden. Verwendet wird die erwartungstreue Schätzfunktion: der Stichprobenmittelwert ${\overline {X}}$ .

Zentrales Schwankungsintervall von $\overline {X}$

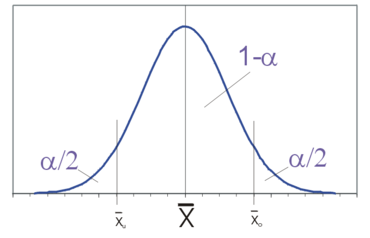
Der Erwartungswert der Grundgesamtheit wird anhand unserer Stichprobe geschätzt

Schätzfunktion: ${\overline {X}}={\frac {1}{n}}\sum _{i=1}^{n}X_{i}$

Punktschätzung: ${\hat {\mu }}={\overline {x}}={\frac {1}{n}}\sum _{i=1}^{n}x_{i}\,,$

wobei die Zufallsvariable $X_{i}$ $(i=1,\dotsc ,n)$ für die i-te Beobachtung (vor der Ziehung der Stichprobe) steht. Der Stichprobenmittelwert folgt einer Normalverteilung mit Erwartungswert $\mu$ und Varianz $\operatorname {Var} ({\overline {X}})={\frac {\sigma ^{2}}{n}}$ (siehe Stichprobenmittel#Eigenschaften)

${\overline {X}}\sim {\mathcal {N}}\left(\mu ,{\frac {\sigma ^{2}}{n}}\right)\,$ .

Die Grenzen des zentralen Schwankungsintervalls

$[{\overline {x}}_{u};{\overline {x}}_{o}]$ ,

das $\mu$ mit der Wahrscheinlichkeit $1-\alpha$ überdeckt, bestimmen sich aus der Beziehung

$P({\overline {x}}_{u}\leq {\overline {X}}\leq {\overline {x}}_{o})=1-\alpha$ .

Man standardisiert zur Standardnormalverteilung ${\mathcal {N}}(0,1)$ und erhält für die standardisierte Zufallsvariable

$Z={\frac {{\overline {X}}-\mu }{\sigma /{\sqrt {n}}}}$

die Wahrscheinlichkeit

$P\left({-z_{\left(1-{\tfrac {\alpha }{2}}\right)}\leq {\frac {{\overline {X}}-\mu }{\sigma /{\sqrt {n}}}}\leq z_{\left(1-{\tfrac {\alpha }{2}}\right)}}\right)=1-\alpha$ ,

wobei $\textstyle z_{\left(1-{\frac {\alpha }{2}}\right)}$ das $(1-{\tfrac {\alpha }{2}})$ -Quantil der Standardnormalverteilung ist. Löst man nach dem unbekannten Parameter $\mu$ auf, so ergibt sich aus

$P\left({{\overline {X}}-z_{\left(1-{\tfrac {\alpha }{2}}\right)}{\frac {\sigma }{\sqrt {n}}}\leq \mu \leq {\overline {X}}+z_{\left(1-{\tfrac {\alpha }{2}}\right)}{\frac {\sigma }{\sqrt {n}}}}\right)=1-\alpha$

das $(1-\alpha)$ -Konfidenzintervall für $\mu$

Mögliche Lage des unbekannten Parameter $\mu$ im Schätzintervall um das beobachtete $\overline x$ .

$KI_{1-\alpha }(\mu )=\left[{{\overline {X}}-z_{\left(1-{\tfrac {\alpha }{2}}\right)}{\frac {\sigma }{\sqrt {n}}};\ {\overline {X}}+z_{\left(1-{\tfrac {\alpha }{2}}\right)}{\frac {\sigma }{\sqrt {n}}}}\right].$

Das Schätzintervall, die Realisierung eines Konfidenzintervalles anhand einer konkreten Stichprobe, ergibt sich dann als

$\left[{{\overline {x}}-z_{\left(1-{\tfrac {\alpha }{2}}\right)}{\frac {\sigma }{\sqrt {n}}};\ {\overline {x}}+z_{\left(1-{\tfrac {\alpha }{2}}\right)}{\frac {\sigma }{\sqrt {n}}}}\right].$

Die Grenzen des Schätzintervalles hängen jedoch von $\overline x$ ab und ändern sich damit von Stichprobe zu Stichprobe. Ist die Stichprobe aber extrem ausgefallen, überdeckt das Intervall den Parameter nicht. Dies ist in α × 100 % aller Stichproben der Fall, d. h., das durch $\overline x$ bestimmte Intervall überdeckt den wahren Parameter $\mu$ also mit einer Wahrscheinlichkeit von $1-\alpha$ .

Von besonderem Interesse ist die Breite des Konfidenzintervalls. Diese bestimmt sich durch die Standardabweichung der Schätzfunktion und das gewählte Konfidenzniveau. Durch Erhöhung des Stichprobenumfangs kann die Breite verringert werden. Erwünscht ist in der Regel ein möglichst schmales Konfidenzintervall, denn dies weist bei konstantem Konfidenzniveau auf eine genaue Schätzung hin.

Als absoluter Fehler wird die halbe Breite des Konfidenzintervalls bezeichnet. Im obigen Fall gilt also

$e=z_{\left(1-{\frac {\alpha }{2}}\right)}{\frac {\sigma }{\sqrt {n}}}\,.$

Der absolute Fehler ist ein Maß für die Genauigkeit der Schätzung (Breite des Konfidenzintervalls: ).

Der absolute Fehler ist von Bedeutung, wenn bei einem gegebenen Konfidenzintervall und einer gegebenen Konfidenzintervalllänge der benötigte Stichprobenumfang ermittelt werden soll. Die Frage lautet also: Welchen Stichprobenumfang benötigt man, um einen Parameter (z.B. arithmetisches Mittel) mit vorgegebener Genauigkeit und vorgegebenem Sicherheitsgrad zu schätzen?

Enthält die zugrundeliegende Stichprobe korrelierte Daten, so ist dies in der Schätzung der Standardabweichung $\sigma$ zu berücksichtigen. Wird dies nicht berücksichtigt, so stößt man auf das Problem der Pseudoreplikation.

Pseudoreplikation wegen korrelierter Daten: ohne Berücksichtigung der Korrelation ist das 90 % Konfidenzintervall des Stichprobenmittelwertes zu klein. Blocking kann für eine bessere Schätzung von $\sigma$ verwendet werden.

Ausgewählte Schätzintervalle

Übersicht für stetige Verteilungen

Eine Übersicht über alle Fälle bei normalverteilten Merkmalen findet sich im Artikel Normalverteilungsmodell.

Erwartungswert eines normalverteilten Merkmals mit bekannter Varianz $\sigma ^{2}$ : $\textstyle z_{(1-{\tfrac {\alpha }{2}})}$ ist das $(1-\alpha /2)$ -Quantil der Standardnormalverteilung.	$\left[{{\overline {x}}-z_{(1-{\tfrac {\alpha }{2}})}{\frac {\sigma }{\sqrt {n}}}\ ;\ {\overline {x}}+z_{(1-{\tfrac {\alpha }{2}})}{\frac {\sigma }{\sqrt {n}}}}\right]$
Erwartungswert eines normalverteilten Merkmals mit unbekannter Varianz: Die Varianz der Grundgesamtheit wird durch die korrigierte Stichprobenvarianz $s^{2}={\tfrac {1}{n-1}}\sum (x_{i}-{\overline {x}})^{2}$ geschätzt. $\textstyle t_{(1-{\tfrac {\alpha }{2}};n-1)}$ ist das $(1-\alpha /2)$ -Quantil der t-Verteilung mit Freiheitsgraden. Für kann das Quantil der t-Verteilung näherungsweise durch das entsprechende Quantil der Standardnormalverteilung ersetzt werden.	$\left[{{\overline {x}}-t_{(1-{\tfrac {\alpha }{2}};n-1)}{\frac {s}{\sqrt {n}}}\ ;\ {\overline {x}}+t_{(1-{\tfrac {\alpha }{2}};n-1)}{\frac {s}{\sqrt {n}}}}\right]$
Erwartungswert eines unbekannt verteilten Merkmals mit unbekannter Varianz: Falls genügend groß ist, kann aufgrund des zentralen Grenzwertsatzes das Konfidenzintervall bestimmt werden.	$\left[{{\overline {x}}-z_{(1-{\tfrac {\alpha }{2}})}{\frac {s}{\sqrt {n}}}\ ;\ {\overline {x}}+z_{(1-{\tfrac {\alpha }{2}})}{\frac {s}{\sqrt {n}}}}\right]$
Standardabweichung eines normalverteilten Merkmals: ${\mathcal {\chi }}_{(p;k)}^{2}$ ist das p-Quantil der Chi-Quadrat-Verteilung mit Freiheitsgraden.	$\left[\ s{\sqrt {\frac {n-1}{\chi _{(1-{\tfrac {\alpha }{2}};n-1)}^{2}}}};s{\sqrt {\frac {n-1}{\chi _{({\tfrac {\alpha }{2}};n-1)}^{2}}}}\ \right]$

Diskrete Verteilungen

Konfidenzintervalle für den Parameter p der Binomialverteilung sind beschrieben in dem

Das sogenannte Clopper-Pearson-Konfidenzintervall kann mit Hilfe der Beta- oder F-Verteilung bestimmt werden. Dieses Konfidenzintervall wird auch exakt genannt, da das geforderte Konfidenzniveau tatsächlich eingehalten wird. Bei Näherungsmethoden, die (meistens) auf der Approximation der Binomialverteilung durch die Normalverteilung basieren, wird das Konfidenzniveau oft nicht eingehalten.

Ist die Zahl der Elemente in der Grundgesamtheit bekannt, kann für den Parameter (mit Hilfe eines Korrekturfaktors) auch ein Konfidenzintervall für ein Urnenmodell ohne Zurücklegen angegeben werden.

Konfidenzintervalle und Hypothesentests

Die Begriffe Konfidenzbereich und statistischer Test sind dual zueinander, unter allgemeinen Bedingungen können aus einem Konfidenzbereich für einen Parameter statistische Tests für entsprechende Punkthypothesen gewonnen werden und umgekehrt:

Testet man von einem Parameter $\vartheta$ die Nullhypothese: $\vartheta =\vartheta _{0}$ , dann wird die Nullhypothese bei einem Signifikanzniveau $\alpha$ nicht abgelehnt, wenn das entsprechende $(1-\alpha)$ -Konfidenzintervall, berechnet mit den gleichen Daten, den Wert $\vartheta_0$ enthält. Daher ersetzen Konfidenzintervalle gelegentlich auch Hypothesentests.

Beispielsweise testet man in der Regressionsanalyse, ob im multiplen linearen Regressionsmodell mit der geschätzten Regressionshyperebene

${\hat {y}}=b_{0}+b_{1}\,x_{1}+b_{2}\,x_{2}+\ldots +b_{k}\,x_{k}$

die wahren Regressionskoeffizienten $\beta _{j}\ (j=1,\ldots ,k)$ gleich Null sind (siehe Globaler F-Test). Wenn die Hypothese nicht abgelehnt wird, sind die entsprechenden Regressoren $x_{j}\ (j=1,\ldots ,k)$ vermutlich für die Erklärung der abhängigen Variablen unerheblich. Eine entsprechende Information liefert das Konfidenzintervall für einen Regressionskoeffizienten: Überdeckt das Konfidenzintervall die Null $\left(0\in KI_{1-\alpha }(\beta _{j})\right)$ , so ist bei einem Signifikanzniveau $\alpha$ der Regressionskoeffizient statistisch nicht verschieden von $0$ .

Beispiele für ein Konfidenzintervall

Beispiel 1

Ein Unternehmen möchte ein neues Spülmittel einführen. Um die Käuferakzeptanz auszuloten, wird das Spülmittel in einem Test-Supermarkt platziert. Mit dieser Aktion soll der durchschnittliche tägliche Absatz in einem Supermarkt dieser Größe geschätzt werden. Man definiert nun den täglichen Absatz als Zufallsvariable [Stück] mit den unbekannten Parametern Erwartungswert $\mu$ und Varianz $\sigma ^{2}$ . Man geht auf Grund langjähriger Beobachtungen hier davon aus, dass annähernd normalverteilt ist. Die Marktforschungsabteilung hat ein Konfidenzniveau von 0,95 (95 %) als ausreichend erachtet. Dann wird 16 Tage lang der tägliche Absatz erfasst. Es ergibt sich

Tag	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
Absatz	110	112	106	90	96	118	108	114	107	90	85	84	113	105	90	104

Bei normalverteilter Grundgesamtheit mit unbekannter Varianz wird das Konfidenzintervall für den Erwartungswert angegeben als

$\left[{{\overline {x}}-t_{\left(1-{\frac {\alpha }{2}};n-1\right)}{\frac {s}{\sqrt {n}}}\ ;\ {\overline {x}}+t_{\left(1-{\frac {\alpha }{2}};n-1\right)}{\frac {s}{\sqrt {n}}}}\right]$

Es ist das Mittel der Stichprobe

${\overline {x}}={\frac {1}{16}}\cdot (110+112+\dotsb +104)={\frac {1}{16}}\cdot 1632=102$

und die Varianz der Stichprobe

${\begin{aligned}s^{2}&={\frac {1}{n-1}}\sum _{i=1}^{n}(x_{i}-{\overline {x}})^{2}\\&={\frac {1}{15}}\left((110-102)^{2}+(112-102)^{2}+\dotsb +(104-102)^{2}\right)\\&={\frac {1}{15}}\cdot 1856=123{,}73\end{aligned}}$

Es ist das $(1-\alpha /2)$ -Quantil der t-Verteilung mit 15 Freiheitsgraden

$t_{\left(1-{\frac {\alpha }{2}};n-1\right)}=t_{\left(0{,}975;15\right)}=2{,}131$

Der Wert für t ist nicht trivial zu errechnen und muss daher aus einer Tabelle abgelesen werden.

Das 95-%-Konfidenzintervall berechnet sich dann als

$\left[{102-2{,}131{\frac {\sqrt {123{,}73}}{\sqrt {16}}};102+2{,}131{\frac {\sqrt {123{,}73}}{\sqrt {16}}}}\right]=[102-5{,}93;102+5{,}93]=[96{,}07;107{,}93]$

Im Mittel enthalten 95 % der so geschätzten Intervalle den wahren Mittelwert $\mu$ , also den durchschnittlichen Tagesabsatz an Spülmittelflaschen in vergleichbaren Supermärkten. Für dieses konkrete Intervall trifft die Aussage, dass es mit 95 % Wahrscheinlichkeit den wahren Mittelwert enthält, jedoch nicht zu. Man weiß lediglich, dass dieses Intervall aus einer Menge (von Intervallen) stammt, von denen 95 % den wahren Mittelwert enthalten.

Beispiel 2

Ein Unternehmen lieferte ein Los (eine Charge) von 6000 Stück (z.B. Schrauben) an den Kunden. Dieser führt mittels Stichprobennahme gemäß der internationalen Norm ISO 2859-1 eine Eingangsprüfung durch. Dabei werden z.B. 200 Schrauben (je nach gewähltem AQL) zufällig über das gesamte Los gezogen und auf Übereinstimmung mit den vereinbarten Anforderungen (Qualitätsmerkmalen) geprüft. Von den 200 geprüften Schrauben erfüllen 10 Stück die gestellten Anforderungen nicht. Mittels der Berechnung des Konfidenzintervalls (Excel-Funktion BETAINV) kann der Kunde abschätzen, wie groß der zu erwartende Anteil fehlerhafter Schrauben im ganzen Los ist: bei einem Konfidenzniveau von 95 % berechnet man das Clopper-Pearson-Konfidenzintervall [2,4 %, 9 %] für den Anteil fehlerhafter Schrauben im Los (Parameter: n=200, k=10).

Literatur

Ulrich Krengel: Einführung in die Wahrscheinlichkeitstheorie und Statistik. 8. Auflage. Vieweg, 2005.
Joachim Hartung: Statistik. 14. Auflage. Oldenbourg, 2005.

Basierend auf einem Artikel in:

Wikipedia.de