Realisierung (Stochastik)
Eine (zufällige) Realisierung, gelegentlich auch fälschlicherweise Realisation genannt, ist ein Begriff aus der Stochastik, einem Teilgebiet der Mathematik. Als Realisierung bezeichnet man dort einen konkreten Wert, den eine Zufallsvariable annimmt, vergleichbar einem Funktionswert einer Funktion für ein gegebenes Argument. Beschreibt die Zufallsvariable einen fairen Würfel, so entspräche eine Realisierung dieser Zufallsvariable einer gewürfelten Augenzahl. Zufallsvariablen werden i.d.R. mit Großbuchstaben und ihre Realisierungen mit Kleinbuchstaben notiert.
Definition
Gegeben sei eine Zufallsvariable
auf einem Wahrscheinlichkeitsraum
.
Dann heißt für
eine Realisierung von .
Beispiele und Verwendung
Ist
eine binomialverteilte
Zufallsvariable zu den Parametern
und
,
so wäre jede natürliche Zahl kleiner oder gleich
eine mögliche Realisierung. Ist
normalverteilt,
so ist jede reelle Zahl eine mögliche Realisierung.
In der mathematischen Statistik spielen Realisierungen von Zufallsvariablen eine wichtige Rolle. Dort werden Stichproben als Realisierung einer Zufallsvariable mit unbekannter Verteilung aufgefasst. Ausgehend von dieser Realisierung wird dann versucht, Aussagen über die Verteilung der Zufallsvariable zu treffen.
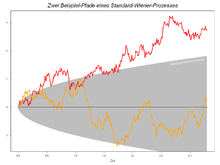
In der Theorie stochastischer Prozesse treten die den Realisierungen ähnlichen Pfade auf, die unter anderem zur Veranschaulichung von Prozessen genutzt werden. Die auftretenden Bildräume sind dann sehr groß. Dementsprechend sind die Realisierungen nicht eine Zahl, sondern eine stetige Funktion oder ähnliches.
Literatur
- David Meintrup, Stefan Schäffler: Stochastik. Theorie und Anwendungen. Springer-Verlag, Berlin Heidelberg New York 2005, ISBN 978-3-540-21676-6.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 23.03. 2021