Arrheniusgraph
Als Arrheniusgraphen (auch Arrheniusdarstellung oder Arrheniusplot) bezeichnet man eine graphische Darstellung, bei der die Werte einer Messgröße (z.B. die Geschwindigkeitskonstante einer chemischen Reaktion) logarithmisch gegen den Kehrwert der Temperatur aufgetragen werden. Dadurch werden exponentiell von der reziproken Temperatur abhängige Werte auf eine Gerade abgebildet; so entsteht die lineare Darstellung einer Funktion in transformierten Koordinaten.
Anwendung
| EA | Aktivierungsenergie | J mol−1 |
| kB | Boltzmann-Konstante | 1,381·10−23 J·K−1 |
| R | universelle Gaskonstante | 8,314 J mol−1·K−1 |
| NA | Avogadro-Konstante | 6,022·1023·mol−1 |
| T | absolute Temperatur | K |
Verwendet wird diese Art der Auftragung bei chemischen oder physikalischen Vorgängen, deren mathematische Beschreibung die Boltzmann-Konstante in der Form
(einzelne Teilchen, siehe Boltzmann-Faktor)
oder
(makroskopische Ebene)
als Term enthält.
In dieser Darstellung erscheint die Abhängigkeit der Messgröße von der Temperatur als Gerade, deren Steigung umgekehrt proportional zur Aktivierungsenergie EA ist. Bezogen auf die Geradengleichung
entspricht die Steigung
dem Ausdruck
und der Kehrwert der Temperatur
dem x-Wert.
Beispiele
|
2 NO2 → 2 NO + O2 |
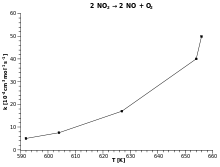
Temperaturauftragung |

Arrheniusgraph |
Naturgesetze, die im Arrheniusplot linear dargestellt werden, sind die Temperaturabhängigkeit der Reaktionsgeschwindigkeit (Arrhenius-Gleichung), des Diffusionskoeffizienten in festen Stoffen sowie der Ladungsträgerdichte in Halbleitern. Nimmt man den natürlichen Logarithmus der Arrheniusgleichung:
kann die Aktivierungsenergie nach
aus der Geradensteigung errechnet werden.
Auch wenn aufgrund von experimentellen Beobachtungen eine entsprechende Gesetzmäßigkeit vermutet wird, kann diese Annahme mit Hilfe der Arrheniusdarstellung beurteilt werden.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 02.04. 2021