Beta-Binomialverteilung
Die Beta-Binomialverteilung ist eine spezielle Wahrscheinlichkeitsverteilung
in der Stochastik. Sie zählt zu den
diskreten
Wahrscheinlichkeitsverteilungen und ist univariat.
Sie kann als eine Art Verallgemeinerung der Binomialverteilung
angesehen werden, da in dieser die Wahrscheinlichkeit von
Erfolgen auf
bei gegebener Wahrscheinlichkeit eines Einzelerfolges angegeben wird, während in
der Beta-Binomialverteilung die Erfolgswahrscheinlichkeit nur ungenau bekannt
ist und durch eine Betaverteilung
B(a,b) beschrieben wird. Es handelt sich somit um eine Mischverteilung.
Die Beta-Binomialverteilung hat drei Parameter: n, a, b
Definition
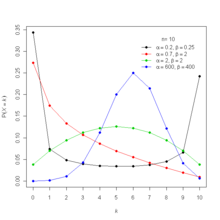

Eine Zufallsvariable
hat eine Beta-Binomialverteilung mit den Parametern
,
und
,
in Zeichen
,
wenn sie für alle
aus dem Träger
die Wahrscheinlichkeitsfunktion
hat, wobei
die Betafunktion
ist.
Konstruktion
Ist
die Wahrscheinlichkeitsfunktion der Binomialverteilung und
die Dichte der Beta-Verteilung, so berechnet sich die
Wahrscheinlichkeitsfunktion der Mischverteilung als
.
Das Integral entspricht genau der obigen Wahrscheinlichkeitsfunktion.
Alternative Darstellung
Alternativ lässt sich die Wahrscheinlichkeitsfunktion auch darstellen als
Dabei ist die Konstante C eine Normierungskonstante und wird folgendermaßen berechnet:
Dabei ist
die Gammafunktion.
Eigenschaften
Erwartungswert
Der Erwartungswert hängt von allen drei Parametern ab:
Varianz
Die Varianz ist:
Schiefe
Die Schiefe wird angegeben mit
Wahrscheinlichkeitserzeugende Funktion
Die wahrscheinlichkeitserzeugende Funktion der Beta-Binomialverteilung ist
.
Hierbei ist
die gaußsche
hypergeometrische Funktion.
Charakteristische Funktion
Durch Substitution folgt daraus die charakteristische Funktion:
.
Momenterzeugende Funktion
Damit ist die momenterzeugende Funktion
.
Spezialfälle
Falls
und
,
dann handelt es sich um eine diskrete
Gleichverteilung mit
,
da der Träger
Werte beinhaltet.
Anwendungsbereiche
Die Beta-Binomialverteilung wird typischerweise in Fällen angewendet, bei denen man üblicherweise eine Binomialverteilung benutzen würde, aber nicht davon ausgehen kann, dass alle Einzelereignisse dieselbe Wahrscheinlichkeit haben einzutreten, sondern diese Wahrscheinlichkeiten mehr oder minder glockenförmig um einen Wert liegen.
Will man zum Beispiel wissen, wie viele Glühlampen innerhalb der nächsten 12 Monaten ausfallen werden, geht aber davon aus, dass die Wahrscheinlichkeit eines Ausfalls einer Glühlampe zwischen verschiedenen Lieferkartons abweicht, dann ist eine Beta-Binomialverteilung angebracht.
Empirisch kann man vermuten, mit einer Beta-Binomialverteilung zu tun zu haben, obwohl man eher an ein Binomialmodell denken würde, falls die Daten mehr streuen als von der Binomialverteilung vorgesehen.
Beispiel
Modell in der bayesschen Statistik
Eine Urne enthält eine
unbekannte Anzahl von Bällen, von denen man aus anderen Stichproben weiß, dass
der Anteil roter Bälle von einer Betaverteilung
beschrieben wird.
Es sollen n-mal Bälle gezogen werden (mit Zurücklegen). Die
Wahrscheinlichkeit, dass x-mal ein roter Ball gezogen wird, ist in der
Beta-Binomialverteilung .
Zahlenbeispiel
Ausgehend von einer kompletten Unwissenheit der apriori Verteilung, die mit
einer
beschrieben wird (Alternativen sind z.B.
),
wird eine "Vorstudie" mit einer Ziehung (mit Wiederholung) von 15 Bällen
organisiert. Einer dieser Bälle ist rot. Somit wird die a posteriori Verteilung
mit der
beschrieben.
Die eigentliche "Studie" sieht eine Ziehung von 40 Bällen vor. Gefragt ist die Wahrscheinlichkeit, dass genau zwei Mal ein roter Ball gezogen wird.
Da in dieser zweiten Ziehung die Wahrscheinlichkeit
jene einer
ist, lässt sie sich wie folgt berechnen:
,
wobei
und da
und außerdem allgemein
ist, erhält man
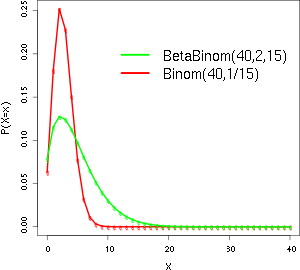
Dieses Ergebnis weicht wesentlich von jenem, welches mit einer „einfachen“
Binomialverteilung
berechnet worden wäre, ab. In diesem Fall wäre das Ergebnis
.
Aus der Grafik wird ersichtlich, dass die „einfache“ Binomialverteilung
weniger Ergebnisse „zulässt“ als die
.
Dies geschieht, da man in dem bayesschen Modell nicht vernachlässigt, dass der
„wahre“ Anteil an roten Bällen im Grunde unbekannt ist, und somit die Ergebnisse
stärker streuen.
Literatur
- Leonhard Held: Methoden der statistischen Inferenz. Likelihood und Bayes, Unter Mitwirkung von Daniel Sabanés Bové, Spektrum Akademischer Verlag Heidelberg 2008, ISBN 978-3-8274-1939-2.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 03.02. 2022