Delta-Distribution

Die Delta-Distribution (auch δ-Funktion; Dirac-Funktion, -Impuls, -Puls, -Stoß (nach Paul Dirac), Stoßfunktion, Nadelimpuls, Impulsfunktion oder Einheitsimpulsfunktion genannt) als mathematischer Begriff ist eine spezielle irreguläre Distribution mit kompaktem Träger. Sie hat in der Mathematik und Physik grundlegende Bedeutung. Ihr übliches Formelsymbol ist δ (kleines Delta).

Definition

Die Delta-Distribution ist eine stetige lineare Abbildung von einem Funktionenraum der Testfunktionen ${\mathcal {E}}$ in den zugrunde liegenden Körper $\mathbb {K}$ :

$\delta\colon\,\mathcal{E}\to\mathbb{K}\,,\,f\mapsto f(0)$ .

Der Testfunktionenraum für die Delta-Distribution ist der Raum der beliebig oft differenzierbaren Funktionen $C^\infty (\Omega)$ mit $\Omega \subset \mathbb{R}^n$ bzw. $\Omega \subset \mathbb{C}^n$ offen und $0 \in \Omega$ . Somit entspricht $\mathbb {K}$ entweder den reellen $\mathbb {R}$ oder den komplexen Zahlen $\mathbb {C}$ .

Die Delta-Distribution ordnet jeder beliebig oft differenzierbaren Funktion eine reelle bzw. komplexe Zahl $\delta(f)=f(0)$ zu, nämlich die Auswertung der Funktion an der Stelle 0. Der Wert, den die Delta-Distribution nach Anwendung auf eine Testfunktion $f\in\mathcal{E}$ liefert, schreibt man (mit der Notation der dualen Paarung) auch als

$\delta(f) = \langle\delta,f\rangle = f(0)$

beziehungsweise auch als

$\delta(f) = \int_{\Omega}\delta(x)\, f(x)\,\mathrm{d}x=f(0)\, .$

Diese Schreibweise ist eigentlich nicht richtig und nur symbolisch zu verstehen, weil die Delta-Distribution eine irreguläre Distribution ist, das heißt, sie lässt sich nicht durch eine lokal integrierbare Funktion in obiger Weise darstellen. Es gibt also keine Funktion $\delta$ , welche der obigen Definition genügt (für Beweis siehe unten „Irregularität“). Insbesondere bei technisch orientierten Anwendungen des Konzepts sind dennoch mathematisch nicht präzise Bezeichnungen wie „Delta-Funktion“, „Dirac-Funktion“ oder „Impulsfunktion“ gebräuchlich. Bei Verwendung der Integral-Schreibweise ist zu beachten, dass es sich nicht um ein Riemann-Integral oder Lebesgue-Integral bzgl. des Lebesgue-Maßes, sondern um die Auswertung des Funktionals $\delta$ an der Stelle , also $\delta(f) = f(0)$ , handelt.

Definition über Dirac-Maß

Das durch ein positives Radon-Maß $\mu$ erzeugte Funktional $\textstyle \langle\mu,f\rangle=\int f(x)\,\mathrm{d}\mu$ (für $f\in\mathcal{D}$ ) ist eine Distribution. Die Delta-Distribution wird von folgendem Radon-Maß – man spricht hier speziell vom Diracmaß – erzeugt:

$\delta(A)=\begin{cases} 1\ & \text{falls }0\in A\\ 0\ & \text{sonst}\end{cases}\ ,\quad A\subset\mathbb{R}$

Ein Maß lässt sich physikalisch interpretieren, z.B. als Massenverteilung oder Ladungsverteilung des Raums. Dann entspricht die Delta-Distribution einem Massenpunkt der Masse 1 oder einer Punktladung der Ladung 1 im Ursprung.

$\langle\delta,f\rangle=\int f(x)\,\mathrm{d}\delta=f(0)$

Befinden sich an den Stellen $x_i\in\mathbb{R}$ Punktladungen $q_{i}$ , wobei die Summe über alle Ladungen endlich bleibt, dann wird für $A\subset\mathbb{R}$ ein Maß auf der $\sigma$ -Algebra aller Teilmengen von $\mathbb {R}$ definiert, das der Ladungsverteilung entspricht ( i_A durchlaufe alle mit $x_{i}\in A$ ):

$\rho(A):=\sum_{i_{A}}q_{i}$

Für dieses Maß ist dann die zugehörige Distribution:

$\langle\rho,f\rangle=\int f(x)\,\mathrm{d}\rho=\sum_{i_{A}}f(x_{i})q_{i}$

Approximation der Delta-Distribution

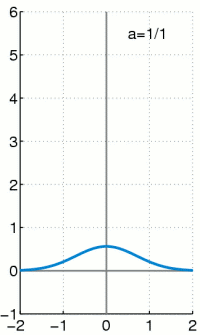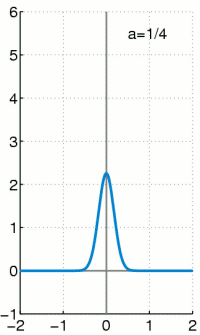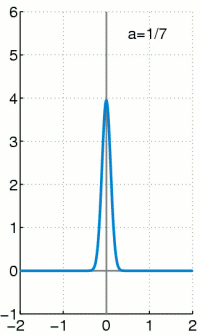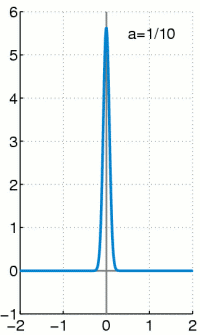
Dichte einer zentrierten Normalverteilung $\delta_{a}(x)=\tfrac {1}{\sqrt{\pi}a} \cdot e^{-\frac {x^2}{a^2}}$ .
Für $a\to 0$ wird die Funktion immer höher und schmaler, der Flächeninhalt bleibt jedoch unverändert 1.

Man kann die Delta-Distribution wie alle anderen Distributionen auch als Grenzwert einer Funktionenfolge darstellen. Die Menge der Dirac-Folgen ist die wichtigste Klasse von Funktionenfolgen, mit denen die Delta-Distribution dargestellt werden kann. Jedoch gibt es noch weitere Folgen, die gegen die Delta-Distribution konvergieren.

Dirac-Folge

Eine Folge $(\delta_k)_{k \in \N}$ integrierbarer Funktionen $\delta_{k} \in L^1(\R^n)$ wird Dirac-Folge genannt, falls

für alle $x\in \mathbb {R} ^{n}$ und alle $k\in \mathbb {N}$ die Bedingung $\delta_{k}(x)\geq 0\,,$
für alle $k\in \mathbb {N}$ die Identität $\int_{\R^n}\delta_{k}(x)\,\mathrm{d}x=1$ und
für alle $\epsilon >0$ die Gleichheit $\lim_{k \to \infty} \int_{\R^n \setminus B_\epsilon (0)} \delta_{k}(x) \mathrm{d} x = 0$

gilt. Manchmal versteht man unter einer Dirac-Folge auch nur einen Spezialfall der hier definierten Dirac-Folge. Wählt man nämlich eine Funktion $\phi \in L^1(\R^n)$ mit $\phi (x)\geq 0$ für alle $x\in \mathbb {R} ^{n}$ und $\textstyle \int_{\R^n} \phi(x) \mathrm{d} x = 1$ und setzt $\delta_\epsilon(x) := \epsilon^{-n} \phi(\tfrac{x}{\epsilon})$ für $\epsilon >0$ , dann erfüllt diese Funktionenschar die Eigenschaften 1 und 2. Betrachtet man den Grenzwert $\epsilon \to 0$ anstatt $k \to \infty$ , so ist auch Eigenschaft 3 erfüllt. Daher nennt man die Funktionenschar $\delta_\epsilon$ ebenfalls Dirac-Folge.

Bemerkungen

Die Funktion $\delta_{k}$ kann man nun mit einer regulären Distribution

$\delta_k(f) := \langle\delta_{k},f\rangle := \int_{\R^n}\delta_{k}(x)\, f(x)\,\mathrm{d}x$

identifizieren. Nur im Limes $k \to \infty$ erhält man das ungewöhnliche Verhalten der Delta-Distribution

$\lim_{k\to \infty} \delta_k(f) = \lim_{k\to \infty} \langle\delta_{k},f\rangle=f(0)=\langle\delta,f\rangle$

wobei zu beachten ist, dass die Limes-Bildung nicht unter dem Integral, sondern davor erfolgt. Würde man den Limes unter das Integral ziehen, so wäre $\delta_{\epsilon}$ fast überall Null, nur nicht bei x=0 . Ein einzelner Punkt hat jedoch das Lebesgue-Maß Null und das ganze Integral würde verschwinden.

Anschaulich stellt man sich die Delta-Distribution als eine beliebig hohe und beliebig schmale Funktion vor, die über der x-Achse eine Fläche mit Größe 1 Flächeneinheit einschließt. Man lässt nun die Funktion immer schmaler und dafür immer höher werden – die Fläche darunter muss konstant 1 bleiben. Es existieren auch mehrdimensionale Dirac-Distributionen, diese werden anschaulich zu mehrdimensionalen „Keulen“ mit dem Volumen 1.

Beispiele für Dirac-Folgen

Im Folgenden werden verschiedene Approximationen (Dirac-Folgen) $\delta_{\epsilon}(x)$ angegeben, zunächst stetig differenzierbare:

Glockenfunktionen (Normalverteilungen)

$\delta_{\epsilon}(x)=\frac{1}{\sqrt{2\pi\epsilon}}\,\exp\left(-\frac{x^{2}}{2\epsilon}\right)$

Die angegebenen Funktionen besitzen ein sehr schmales und sehr hohes Maximum bei x=0, die Breite ist etwa $\sqrt{\epsilon}\to 0$ und die Höhe etwa $1/\sqrt{\epsilon}\to\infty$ . Für alle $\epsilon$ ist der Flächeninhalt unter der Funktion 1.

Lorentzkurven

$\delta_{\epsilon}(x)=\frac{1}{\pi}\frac{\epsilon}{x^{2}+\epsilon^{2}}$

Fresnel-Darstellung

$\delta_{\epsilon}(x)=\frac{1}{\sqrt{i\pi\epsilon}}\,\exp\left(\frac{ix^{2}}{\epsilon}\right)$

die man sich vorstellen kann als eine Linie, die auf einen Zylinder gewickelt ist, und deren Wicklungen durch das $x^{2}$ immer enger werden; die Grundfläche (in --Ausrichtung) des Zylinders wird aus dem Imaginär- und Realteil der Funktion gebildet, die Funktion entwickelt sich dann in -Richtung.

Es sind aber auch Approximationen möglich, die nur stückweise stetig differenzierbar sind:

Rechteckfunktion

$\delta_{\epsilon}(x)=\frac{\textrm{rect}(x/\epsilon)}{\epsilon}=\begin{cases} \frac{1}{\epsilon} & \ |x|\leq\frac{\epsilon}{2}\\ 0 & \ \text{sonst}\end{cases}$

Dreiecksfunktion

$\delta_{\epsilon}(x)=\begin{cases} \frac{\epsilon+x}{\epsilon^{2}} & \ -\epsilon\leq x\leq0\\ \frac{\epsilon-x}{\epsilon^{2}} & \ 0<x\leq\epsilon\\ 0 & \ \text{sonst}\end{cases}$

Exponentialfunktion um Ursprung abfallend

$\delta_{\epsilon}(x)=\frac{1}{2\epsilon}\exp\left(-\frac{|x|}{\epsilon}\right)$

Weitere Beispiele

Approximation durch die Sincfunktion

Die Funktionenfolge der Sinc-Funktionen

$\delta_{\epsilon}(x)=\frac{1}{\pi x}\sin\left(\frac{x}{\epsilon}\right)$
ist keine Dirac-Folge, da ihre Folgenglieder auch negative Werte annehmen. Betrachtet man allerdings den Ausdruck

$\lim_{\epsilon \to 0} \int_{-\infty}^\infty \frac{1}{\pi x}\sin\left(\frac{x}{\epsilon}\right) \phi(x) \mathrm{d} x$

so konvergiert für alle $\phi \in \mathcal{D}$ diese Folge im distributionellen Sinn gegen die Delta-Distribution.

Definition in der Nichtstandardanalysis

In der Nichtstandardanalysis lässt sich eine „Delta-Funktion“ explizit als Funktion mit den gewünschten Eigenschaften definieren. Diese ist zudem auch unendlich oft differenzierbar. Ihre erste Ableitung lautet

${\frac {{\textrm d}}{{\textrm d}x}}\delta (x)=-{\frac {\delta (x)}{x}}$

und ihre -te Ableitung

$\frac{\textrm d^n}{\textrm d^nx} \delta(x) = (-1)^n \frac{n!}{x^n} \delta(x).$

Eigenschaften

Definierende Eigenschaft der Delta-Distribution: Faltungseigenschaft, auch Ausblendeigenschaft, Siebeigenschaft genannt

$\langle\delta,f\rangle=\int_{-\infty}^{\infty}\delta(x)\, f(x)\,\mathrm{d}x=f(0)$

bzw. mit den Eigenschaften Translation und Skalierung (siehe unten) folgt:

$\int_{- \infty}^\infty f(x)\,\delta (x-a)\,\mathrm{d}x=\int_{- \infty}^\infty f(x)\,\delta (a-x)\,\mathrm{d}x=f(a),$

speziell für den Fall der konstanten Funktion 1:

$\int_{- \infty}^\infty \delta (x-a)\,\mathrm{d}x=1$

Linearität:

$\langle\delta,f+g\rangle=\langle\delta,f\rangle+\langle\delta,g\rangle=f(0)+g(0)$

Translation:

$\langle\delta(\cdot-a),f\rangle=\langle\delta,f(\cdot+a)\rangle=f(a)$

für $\delta(\cdot-a)$ ist auch die Bezeichnung $\delta_{a}$ gebräuchlich.

Skalierung:

$\langle\delta(a\cdot),f\rangle=\frac{1}{|a|}\langle\delta,f(\tfrac{\cdot}{a})\rangle=\frac{1}{|a|}f(0)$

und

$\delta(\alpha x) = \frac{1}{|\alpha|} \delta(x)$

das heißt die Delta-Distribution ist positiv homogen vom Grad −1.

Dimension

Eine direkte Folgerung aus der Skalierungseigenschaft ist die Dimension bzw. Maßeinheit der Delta-Distribution. Sie entspricht genau der reziproken Dimension ihres Arguments. Hat beispielsweise die Dimension einer Länge, so hat $\delta(x)$ die Dimension (1/Länge).

Hintereinanderausführung:

$\int_{-\infty}^{\infty}\phi(x)\,\delta(g(x))\,\mathrm{d}x=\sum_{i=1}^{n}\int_{-\infty}^{\infty}\phi(x)\frac{\delta(x-x_{i})}{|g'(x_{i})|}\,\mathrm{d}x=\sum_{i=1}^{n}\frac{\phi(x_{i})}{|g'(x_{i})|},$

$\delta(g(x))=\sum_{i=1}^{n}\frac{\delta(x-x_{i})}{|g^{\prime}(x_{i})|}$

wobei $x_{i}$ die einfachen Nullstellen von g(x)

sind (sofern g(x)

nur endlich viele und nur einfache Nullstellen hat). Damit folgt als ein Spezialfall die Rechenregel

$\delta(x^2 - \alpha^2) = \frac{1}{2|\alpha|} [\delta(x - \alpha)+ \delta(x + \alpha) ],$

Irregularität

Die Irregularität (= Singularität) der Delta-Distribution lässt sich mit einem Widerspruchsbeweis zeigen:

Angenommen $\delta$ wäre regulär, dann gäbe es eine lokal integrierbare Funktion $\delta(x)\in L^{1}_{lok}$ , also eine Funktion, die über jedes kompakte Intervall [a,b] bzgl. des Lebesgue-Maßes integrierbar ist

$\int_{a}^{b}|\delta(x)|\mathrm{d}x<\infty$

so dass für alle Testfunktionen f(x) gilt:

$\langle\delta,f\rangle = \int_{-\infty}^{\infty}\delta(x)\, f(x)\,\mathrm{d}x=f(0)$

Insbesondere muss dies für folgende Testfunktion $\phi_{b}(x)$ mit kompaktem Träger [-b,b] gelten:

$\phi_{b}(x)=\begin{cases}\exp(\frac{b^{2}}{x^{2}-b^{2}}) & |x|<b\\0 & |x|\geq b\end{cases}$

Die Wirkung der Delta-Distribution auf diese ist:

$\langle\delta,\phi_{b}\rangle = \phi_{b}(0)=\exp(-1)=\mathrm{const}_{\,b}$

Mit der angenommenen regulären Distribution

$\langle\delta,\phi_{b}\rangle=\int_{-\infty}^{\infty}\delta(x)\,\phi_{b}(x)\,\mathrm{d}x=\int_{-b}^{b}\delta(x)\,\phi_{b}(x)\,\mathrm{d}x$

lässt sich folgende Abschätzung durchführen:

$\phi_{b}(0)=|\langle\delta,\phi_{b}\rangle|=\left|\int_{-b}^{b}\delta(x)\,\phi_{b}(x)\,\mathrm{d}x\right|\leq\underbrace{\|\phi_{b}(x)\|_{\infty}}_{\phi_{b}(0)}\,\int_{-b}^{b}|\delta(x)|\,\mathrm{d}x\underset{(b<b_{c})}{<}\phi_{b}(0)$

Weil $\delta(x)\in L^{1}_{lok}$ wird das Integral $\textstyle \int_{-b}^{b}|\delta(x)|\,\mathrm{d}x$ für $b<b_{c}$ (wobei b_c ein von der Funktion $\delta(x)$ abhängiger kritischer Wert ist) kleiner 1 (und konvergiert gegen 0 für gegen 0). Man erhält $\phi_{b}(0)<\phi_{b}(0)$ , also einen Widerspruch; somit ist die Delta-Distribution nicht durch eine lokal integrierbare Funktion darstellbar. Der Widerspruch ergibt sich, weil die Menge {0} für das Lebesgue-Maß vernachlässigbar ist, nicht aber für das Dirac-Maß.

Ableitungen

Ableitung der Delta-Distribution

Die Delta-Distribution kann wie jede Distribution beliebig oft distributiv differenziert werden:

$\langle\delta',f\rangle=-\langle\delta,f'\rangle=-f'(0)$

Und die -te distributive Ableitung:

$\langle\delta^{(n)},f\rangle=(-1)^{n}\langle\delta,f^{(n)}\rangle=(-1)^{n}f^{(n)}(0)$

Ableitung der Dirac-Folge

Die Ableitungen der regulären Distributionen $\delta_{\epsilon}$ können mittels partieller Integration berechnet werden (hier exemplarisch für erste Ableitung, analog für höhere)

$\begin{align} \langle\delta_{\epsilon}^{\prime},f\rangle &= \int_{-\infty}^{\infty}\delta_{\epsilon}^{\prime}(x)\, f(x)\,\mathrm{d}x \\ &= \underbrace{\left[\delta_{\epsilon}(x)\, f(x)\right]_{-\infty}^{\infty}}_{=0}-\int_{-\infty}^{\infty}\delta_{\epsilon}(x)\, f^{\prime}(x)\,\mathrm{d}x \\ &= -\int_{-\infty}^{\infty}\delta_{\epsilon}(x)\, f^{\prime}(x)\,\mathrm{d}x \\ &= -\langle\delta_{\epsilon},f^{\prime}\rangle \end{align}$

und ergeben im Limes $\epsilon\to 0$ das Verhalten der distributiven Ableitung:

$\lim_{\epsilon\to0}\langle\delta_{\epsilon}^{\prime},f\rangle=-f^{\prime}(0)=\langle\delta^{\prime},f\rangle$

Ableitung der Heaviside-Distribution

Die Heaviside-Funktion $\Theta (x)$ ist nicht stetig differenzierbar, aber die distributive Ableitung existiert, diese ist nämlich die Delta-Distribution:

$\langle\Theta',f\rangle=-\langle\Theta,f'\rangle=-\int_{-\infty}^{\infty}\Theta(x)\, f'(x)\,\mathrm{d}x=-\int_{0}^{\infty}f'(x)\,\mathrm{d}x=-\underbrace{f(\infty)}_{=0}+f(0)=\langle\delta,f\rangle$

Da die Heaviside-Distribution keinen kompakten Träger hat, müssen hier die Testfunktionen beliebig oft differenzierbare Funktionen mit kompaktem Träger sein $f\in C_0^\infty \cong\mathcal{D}$ , das heißt muss im Unendlichen verschwinden.

Fourier-Laplace-Transformation

Da die Delta-Distribution einen kompakten Träger hat, ist es möglich, die Fourier-Laplace-Transformation dieser zu bilden. Für diese gilt

$\hat{\delta} = 1\,.$

Fourier-Transformation

Die Fourier-Laplace-Transformation ist ein Spezialfall der Fourier-Transformation und somit gilt auch

$\mathcal{F} (\delta)(\phi) = \delta (\mathcal{F}(\phi)) = \delta \left(\int_{-\infty}^\infty e^{-i x \xi} \phi(x) \mathrm{d} x\right) = \langle 1,\phi \rangle \,.$

Es gibt auch die Konvention, den Faktor $\tfrac{1}{\sqrt{2 \pi}}$ mit der Fourier-Transformation zu multiplizieren. In dem Fall ist $\tfrac{1}{\sqrt{2 \pi}}$ ebenfalls das Ergebnis der Fourier-Transformation der Delta-Distribution. Anschaulich bedeutet das Resultat der Transformation, dass in der Delta-Distribution alle Frequenzen enthalten sind, und zwar mit gleicher Stärke. Die Darstellung $\delta(x)=\mathcal{F}^{-1}(1)$ (beziehungsweise $\delta(x)=\mathcal{F}^{-1}(\tfrac{1}{\sqrt{2 \pi}})$ bei der anderen Konvention für den Vorfaktor) ist eine in der Physik wichtige Darstellung der Delta-Distribution.

Laplace-Transformation

Die Laplace-Transformation ${\mathcal {L}}$ der Delta-Distribution erhält man als Spezialfall der Fourier-Laplace-Transformation. Es gilt nämlich auch hier

$\mathcal{L}( \delta) = 1\,.$

Im Gegensatz zur Fourier-Transformation gibt es hier keine anderen Konventionen.

Anmerkung bezüglich der Darstellung

Oftmals werden die Fourier beziehungsweise die Laplace-Transformation durch die gewöhnliche Integralschreibweise dargestellt. Jedoch sind diese Darstellungen

$\mathcal{F}(\delta)(\xi) = \int_{-\infty}^\infty e^{-i \xi x}\,\delta(x)\,\mathrm{d} x$

für die Fourier-Transformation beziehungsweise

$\mathcal{L}(\delta)(\xi)=\int_{0}^{\infty}e^{-\xi x}\,\delta(x)\,\mathrm{d}x$

für die Laplace-Transformation nur symbolisch zu verstehen und mathematisch nicht definiert.

Transformation der verschobenen Delta-Distribution

Es ist ebenfalls möglich die Fourier-Transformation beziehungsweise die Laplace-Transformation für die um a>0 verschobene Delta-Distribution $\delta_a$ zu berechnen. Es gilt

$\begin{align} \mathcal{F}(\delta_a) &= e^{-i \xi a} \\ \mathcal{L}(\delta_a) &= e^{- \xi a}. \end{align}$

Praktische Anwendung

Praktische Bedeutung hat der Dirac-Stoß bei der Ermittlung der Impulsantwort in der Akustik (in anderen Sparten der Physik spricht man auch von einer $\delta$ -Größe, wenn man meint, dass die betreffende Größe einer schmalst-möglichen Verteilung genügt). So hat jeder Raum ein eigenes Schallverhalten. Mit einem Dirac-Impuls (angenähert durch ein Klatschen mit den Händen) kann dieses Verhalten (durch Messen des „Echos“, also der Systemantwort) ermittelt werden.

Typische, technisch realisierbare Dirac-Werte:

Hochspannungstechnik ca. 1–100 ns Halbwertsbreite
Hochfrequenztechnik ca. 10–100 ps Halbwertsbreite
Pulslasertechnik ca. 10–100 fs Halbwertsbreite

Eine wichtige Anwendung der Delta-Distribution ist die Lösung inhomogener linearer Differentialgleichungen mit der Methode der Greenschen Funktion.

Mehrdimensionale Delta-Distribution

Definition

Im Mehrdimensionalen ist der Raum der Testfunktionen ${\mathcal {E}}$ gleich $C^{\infty}(\mathbb{R}^{n})$ , der Raum der beliebig oft total differenzierbaren Funktionen $f\colon\,\mathbb{R}^{n}\to\mathbb{R}$ .

Die Delta-Distribution hat auf die Testfunktion $f\colon\,\mathbb{R}^{n}\to\mathbb{R}$ die folgende Wirkung:

$\delta\colon\,\mathcal{E}\to\mathbb{R}\,,\ f\mapsto f(\vec{0})$

In der informellen Integralschreibweise unter Verwendung von Translation und Skalierung:

$\int f(\vec{x})\,\delta(\vec{x}-\vec{a})\,\mathrm{d}^{n}x=\int f(\vec{x})\,\delta(\vec{a}-\vec{x})\,\mathrm{d}^{n}x=f(\vec{a})$ .

Eigenschaften

Die „mehrdimensionale“ Delta-Distribution lässt sich als Produkt von „eindimensionalen“ Delta-Distributionen schreiben:

$\delta(\vec{x}-\vec{a})=\delta(x_{1}-a_{1})\,\delta(x_{2}-a_{2})\, ... \,\delta(x_{n}-a_{n})$ .

Speziell im Dreidimensionalen gibt es eine Darstellung der Delta-Distribution, die häufig in der Elektrodynamik eingesetzt wird, um Punktladungen darzustellen:

$\delta(\vec{x}-\vec{a})=-\frac{1}{4\pi}\Delta\frac{1}{\|\vec{x}-\vec{a}\|_{2}}$ .

Delta-Distribution in krummlinigen Koordinatensystemen

In krummlinigen Koordinatensystemen muss die Funktionaldeterminante

$\mathrm{d}^{3}r = \mathrm{d}x~\mathrm{d}y~\mathrm{d}z = \det{\frac{\partial(x,y,z)}{\partial(a,b,c)}}~\mathrm{d}a~\mathrm{d}b~\mathrm{d}c$

berücksichtigt werden.

Der Ansatz

$\delta ({{\vec {r}}-{\vec {r}}_{0}})=\gamma (a,b,c)~\delta (a-a_{0})~\delta (b-b_{0})~\delta (c-c_{0})$

mit $\vec{r} = (a,b,c)$ und ${\vec {r}}_{0}=(a_{0},b_{0},c_{0})$ führt dabei auf die Gleichung

$\int _{V}\delta ({\vec {r}}-{\vec {r}}_{0})~\mathrm {d} ^{3}r=\iiint _{V}\det {\frac {\partial (x,y,z)}{\partial (a,b,c)}}~\gamma (a,b,c)~\delta (a-a_{0})~\delta (b-b_{0})~\delta (c-c_{0})~\mathrm {d} a~\mathrm {d} b~\mathrm {d} c~{\stackrel {!}{=}}~1$ , falls ${\vec {r}}_{0}\in V$ .

Daran lässt sich ablesen, dass gelten muss

$\gamma =\left(\left.\det {\frac {\partial (x,y,z)}{\partial (a,b,c)}}\right|_{{\vec {r}}_{0}}\right)^{-1}$ .

In krummlinigen Koordinatensystem muss die Delta-Distribution also mit einem Vorfaktor versehen werden, der dem Kehrwert der Funktionaldeterminante entspricht.

Beispiele

In Kugelkoordinaten mit $\vec{r} = (r, \theta, \phi)$ und ${\vec {r}}_{0}=(r_{0},\theta _{0},\phi _{0})$ gilt:

$\delta ({\vec {r}}-{\vec {r}}_{0})={\frac {1}{r^{2}\sin \theta }}~\delta (r-r_{0})~\delta (\theta -\theta _{0})~\delta (\phi -\phi _{0})$

In Zylinderkoordinaten mit $\vec{r} = (\rho, \phi, z)$ und ${\vec {r}}_{0}=(\rho _{0},\phi _{0},z_{0})$ gilt:

$\delta ({\vec {r}}-{\vec {r}}_{0})={\frac {1}{\rho }}~\delta (\rho -\rho _{0})~\delta (\phi -\phi _{0})~\delta (z-z_{0})$

Siehe auch

Kronecker-Delta

Literatur

Dieter Landers, Lothar Rogge: Nichtstandard Analysis. Springer-Verlag, Berlin u.a. 1994, ISBN 3-540-57115-9 (Springer-Lehrbuch).
Wolfgang Walter: Einführung in die Theorie der Distributionen. 3. vollständig überarbeitete und erweiterte Auflage. BI-Wissenschafts-Verlag, Mannheim u.a. 1994, ISBN 3-411-17023-9.

Basierend auf einem Artikel in:

Wikipedia.de