Radiodrome
Die Radiodrome („Leitstrahlkurve“, v. lat. radius „Strahl“ und griech. dromos „Lauf, Rennen“), oder Hundekurve ist eine spezielle ebene Verfolgungskurve. Sie beschreibt die Bewegung eines Punktes, der einen anderen Punkt verfolgt. Beide Punkte bewegen sich dabei mit konstanter, aber nicht notwendigerweise gleicher Geschwindigkeit.
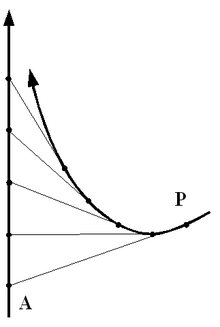
Die „gerade Radiodrome“ beschreibt den einfachen Fall, in dem der Verfolgte sich auf einer Gerade bewegt. Pierre Bouguer beschrieb sie 1732 erstmals. Sie ist eine der Kurven, die mit dem Trivialnamen „Hundekurve“ bezeichnet werden, da sie von einem Hund beschrieben wird, der einen auf einer geraden Linie fliehenden Hasen verfolgt (soweit sich der Standort des Hundes nicht auf dieser Linie befindet). Pierre-Louis Moreau de Maupertuis erweiterte die Problematik bald darauf auf beliebige Leitkurven. Dies führte zur Definition der „allgemeinen Radiodrome“.
Die Kurve tritt typischerweise in Tracking-Problemen in der Robotik und dynamischen Simulationen auf (Verfolgungsprobleme).
Allgemeine Gleichung
Sei
die Bewegung des verfolgten Punktes und
die Verfolgerkurve. Dann hat man die Gleichung
für alle Zeitpunkte ,
wobei
das Skalarprodukt bedeutet.
Diese Gleichung ergibt sich aus der Gleichung
,
welche beschreibt, dass die Tangente in
parallel zur Geraden durch
und
ist (das Skalarprodukt sich also als Produkt der Längen der Vektoren ergibt) und
der Bedingung
.[1]
Spezielle Radiodrome
Gerade Radiodrome
- Bildungsgesetz
- Sei
der Startpunkt eines „Verfolgten“, und
der Startpunkt eines „Verfolgers“.
- Wandert der Punkt
mit der Geschwindigkeit
auf einer Geraden, und bewegt sich der Punkt
mit der Geschwindigkeit
immer in Richtung des Punktes
, dann durchläuft
eine Radiodrome.
- Funktionsgleichung in kartesischen Koordinaten
- Sei weiters das Geschwindigkeitsverhältnis
.
im Ursprung,
auf der x-Achse, A bewege sich entlang der y-Achse. Dann bewegt sich
auf der Kurve
- Den zweiten Fall nennt man eigentliche Radiodrome. Sie stellt den einfachsten Spezialfall dar.
Herleitung
- Für die Bewegung eines Punktes
mit der Geschwindigkeit
auf einem Funktionsgraphen gilt grundsätzlich:
Da hier die Bewegung nach links verlaufen soll,
also abnimmt, ist
negativ. Soll w durch einen positiven Wert dargestellt werden, so verwendet man hier
konstant.
- Ebenfalls grundsätzlich gilt:
sowie
.
- Nun fährt
mit der konstanten Geschwindigkeit
auf der
-Achse nach oben, hat also zum Zeitpunkt
den Wert
. Dann zeigt die Tangente an den gesuchten Graphen von P auf A, und man erhält die Tangentenbedingung
. Das ergibt die Differentialgleichung:
.
- Differentiation
nach
liefert
. Mit dem unter 2. Gesagten ergibt sich daraus
, was sich zu
vereinfacht.
- Ersetzt man nun
nach 1., erhält man
- Die Lösung gelingt mit Integration
durch die Substitution
somit
. Daraus folgt
und durch Trennung der Variablen zu
mit
.
- Integrieren liefert
(siehe arsinh), sowie Rücksubstitution und Anwenden der Definitionsformel des sinh x, mit C1 = eC, zu:
- Hierauf erneutes Integrieren, unter Berücksichtigung von C2
liefert:
- Einsetzen der Startwerte von
bzw.
liefern die Werte für C1 und C2.
E. W. Weisstein gibt in MathWorld eine geschlossene Parameterdarstellung.
- Bemerkungen
, da
- Ist
, also
, so holt der Verfolger
den Verfolgten
ein, der Graph hat also dort einen Schnittpunkt mit der
-Achse. Ist
, also
, so wird
nicht eingeholt, der Graph nähert sich also asymptotisch der
-Achse.
- Ist die Startrichtung nicht normal auf der Leitgeraden, so erhält man
andere Randbedingungen. Der Tiefpunkt errechnet sich aus
.
- Für eine allgemeine Lage der Leitgerade ist eine geeignete Koordinatentransformation vorzunehmen.
- Beispiel
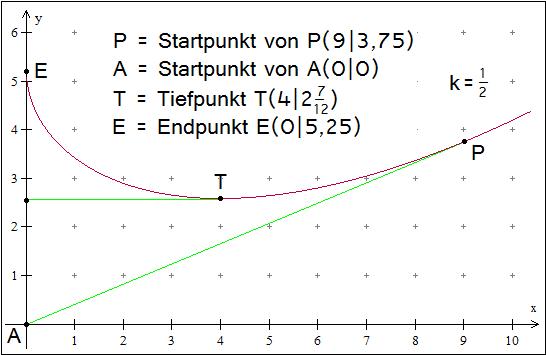
werde von
mit doppelter Geschwindigkeit verfolgt, also
.
Legt man ein Koordinatensystem mit
im Ursprung und
-Achse
in Bewegungsrichtung von
an, senkrecht dazu durch
also die
-Achse,
so möge sich
gerade in
befinden.
bewegt sich nun auf den Ursprung zu, die Tangente der Radiodrome hat also bei
die Steigung
.
Dies eingesetzt in die Gleichung aus 7. liefert mit
:
,
was auf die quadratische Gleichung
mit den Lösungen
bzw.
führt, wobei nur die positive Lösung verwendbar ist (s. 1. Bemerkung). In die
Gleichung für
aus 8. eingesetzt erhält man:
Einsetzen von P(9|3,75) liefert C2=5,25. Damit ergibt sich
mit
Bei
und damit
hat der Graph einen Tiefpunkt, bei
und damit
holt Verfolger
den Verfolgten
ein. Auch die Länge des von
zurückgelegten Weges lässt sich leicht berechnen:
mit der Stammfunktion
.
Der von
von
bis zum Tiefpunkt bei
zurückgelegte Weg beträgt dann
.
Die dort waagerechte Tangente zeigt auf
und hat die Höhe
(s.o.),
hat also den Weg
zurückgelegt, genau die Hälfte von
,
da
halb so schnell ist wie
.
Von
bis
legt
den Weg
zurück,
die Hälfte, also
,
weshalb
bei
von
getroffen wird.
Eigenschaften
- Die Verbindungslinie von entsprechenden
und
ist Tangente an die Radiodrome.
- Offensichtlich ist
nicht negativ für alle
, falls der Startpunkt oberhalb der
-Achse liegt.
Analyse des Geschwindigkeitsparameters
:
- Bei
ist
schneller als
, Die Kurve nähert sich asymptotisch der
-Achse: Der Verfolger ist langsamer und erreicht den Verfolgten nicht, noch kreuzt er seine Bahn.
- Bei gleicher Geschwindigkeit (
) läuft der Verfolger in zunehmend gleichem Abstand hinter dem Verfolgten her: Die Kurve zeigt das Grenzwert-Verhalten einer „Traktrix“.
:
- Es gibt genau einen Endpunkt des Graphen am linken Rand
der Definitionsmenge. Der Verfolger ist schneller als der Verfolgte und erreicht jenen in endlicher Zeit. Wir nennen diesen Punkt „Treffpunkt“ oder „Fangpunkt“, die Kurve ist im Fangpunkt tatsächlich zu Ende.
Der Fall
ist trivial, nämlich eine
Gerade. Der Verfolger ist „unendlich“ schnell, oder der Verfolgte steht still.
Für rationales
degeneriert die Funktion zu einer algebraischen
Kurve – sind beispielsweise
,
so ist diese Kurve vom Grad
.
Kreis-Radiodrome
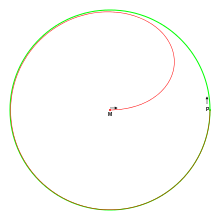
Bewegt sich der „Verfolgte“ auf einer Kreislinie und startet der „Verfolger“ im Mittelpunkt, so ergibt sich eine weitere Version.
Haben Verfolgter und Verfolger die gleiche Geschwindigkeit, so wird der Verfolgte „nach unendlicher Zeit“ eingeholt, d.h. der Abstand zwischen Verfolger und Verfolgtem konvergiert gegen 0.
Falls die Verfolgerkurve eine höhere Geschwindigkeit als die verfolgte Kurve hat, wird sie diese in endlicher Zeit einholen.
Falls die Verfolgerkurve geringere Geschwindigkeit als die verfolgte Kurve hat, wird sie sich einem Kreis mit kleinerem Durchmesser annähern.
Anmerkungen
- ↑
Die Verfolgerkurve soll konstante Geschwindigkeit
haben und nach geeigneter Wahl der Einheiten kann man dann
annehmen.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 06.02. 2022