Venturi-Düse

Eine Venturi-Düse (auch Venturi-Rohr, entwickelt von Giovanni Battista Venturi) besteht aus einem glattwandigen Rohrstück mit einer Verengung des Querschnitts, beispielsweise durch zwei gegeneinander gerichtete Konen, die an der Stelle ihres geringsten Durchmessers vereint sind. An dieser Stelle ist daneben ein Abnahmerohr platziert.

Wirkprinzip

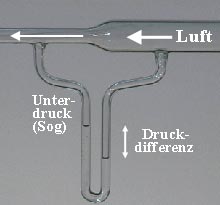
Eine Venturi-Düse wird vom Fluid Luft durchflossen. Die Flüssigkeit im Abnahmerohr zeigt die Druckdifferenz.

Wenn ein Fluid durch eine Venturi-Düse fließt, ist an der engsten Stelle des Rohres der dynamische Druck (Staudruck) maximal und der hydrostatische Druck minimal. Die Geschwindigkeit des Fluids steigt im Verhältnis der Querschnitte beim Einströmen in den engeren Teil an, weil im ganzen Rohr dieselbe Masse pro Zeit durchfließt (Kontinuitätsgesetz). Dadurch sinkt der Druck im Abnahmerohr, das sich im engen Teil befindet. Damit entsteht ein Differenzdruck, der in Messgeräten oder zum Ansaugen von Flüssigkeiten oder Gasen benutzt werden kann.

Die Druckdifferenz ist bei idealen Flüssigkeiten (inkompressibel und reibungsfrei) durch die Bernoulli-Gleichung gegeben. Bei idealen Gasen gilt die erweiterte Bernoulli-Gleichung.

Anwendungen

Venturi-Düsen finden sich heute in der Technik in einer Vielzahl von Anwendungen, da sie wartungsarm und kostengünstig arbeiten. Sie werden in der Aquarientechnik als Abschäumer verwendet ebenso wie in der Chemie als sogenannte Venturi-Injektoren, um Gase in Flüssigkeiten aufzulösen oder als Messwertgeber für Strömungsgeschwindigkeiten von Gasen oder Flüssigkeiten. Außerdem wird dieses Prinzip in Ölern der Aufbereitungseinheit von pneumatischen Anlagen verwendet. Als industrielle Normteile des Maschinenbaues sind Venturi-Düsen als „Hochdruckschweißer“ nach DIN 19215 und ISO 5167 definiert.

Im Folgenden sollen beispielhaft einige Anwendungen dargestellt werden.

Messinstrumente

Das Venturi-Prinzip wird zur Messung der Strömungsgeschwindigkeit von Flüssigkeiten und Gasen angewendet. Das Bild im Abschnitt Wirkprinzip zeigt ein sich verengendes Glasrohr mit von rechts einströmender Luft. Deren Druck ist dort am geringsten, wo der Querschnitt des Rohres am engsten bzw. die Strömungsgeschwindigkeit am höchsten ist. Das Manometer misst die statischen Drücke vor und in der Verengung, deren Differenz von der Strömungsgeschwindigkeit und der Luftdichte abhängt.
Der Durchfluss im Venturi-Rohr mit kritischer Strömung (en. "critical flow Venturi", "sonic nozzles") erreicht im Bereich des Punktes mit dem geringsten Durchmesser Überschallströmung, siehe auch Lavaldüse. Der Massendurchfluss ist direkt proportional zum Eingangsdruck. Diese Anordnung kann als präziser Standard für Durchflussmengen oder als Messgerät eingesetzt werden. Es gibt eine Norm ISO 9300 für diese Düsen.

Vergaser

Autogas-Venturi-Düse

Eine weitere Anwendung findet sich im Motorenbau. Um einen Verbrennungsmotor mit gasförmigem (Autogas bzw. Erdgas) oder flüssigem Brennstoff (z.B. Benzin) zu betreiben, muss dieser mit Sauerstoff aus der Umgebungsluft als Oxidationsmittel vermischt werden. Das Gas wird dabei in einer Venturi-Düse vor der Drosselklappe in der richtigen Menge in den angesaugten Luftstrom eingemischt.

Luftfahrt

Venturi-Rohr an einem Flugzeug

Das Venturi-Rohr war eines der ersten Geräte in der Motorfliegerei, mit dem man Unterdruck erzeugen konnte. Der Doppeltrichter war am Flugzeugrumpf so montiert, dass er genau in der Abströmrichtung des Propellers lag. Mit Hilfe des im Rohr erzeugten Unterdrucks konnten dann die Kreiselinstrumente wie Kreiselkompass (Gyro), künstlicher Horizont und Wendezeiger betrieben werden. In den Anfängen der Fliegerei wurde das Venturi-Rohr auch versuchsweise direkt als Fahrtmesser verwendet.

Das Venturi-Rohr hat für die Fliegerei einen entscheidenden Nachteil. Die Erhöhung der Strömungsgeschwindigkeit der Luft führt zu einer stärkeren Abkühlung derselben. Daher neigt das System sehr leicht zur Vereisung (siehe auch Vergaservereisung). Dieses hat dazu geführt, dass Venturi-Rohre heute in der Fliegerei, außer bei Oldtimern, nicht mehr verwendet werden. Sie sind durch die Suction-Pump (deutsch Unterdruckpumpe) bzw. das Pitotrohr ersetzt worden. Der Wendezeiger wird heute meist von einem Gleichstrommotor angetrieben, um bei Ausfall der Suction-Pump und damit des künstlichen Horizonts weiter korrekt anzuzeigen.

Dekantierausguss für Weinflaschen

Venturi-Dekantierausguss

Als Dekantierausguss für Weinflaschen findet das Venturi-Rohr zur Geschmacksverbesserung von Rotwein Verwendung. Das System ist ein spezieller Ausguss, der auf den Flaschenhals aufgesetzt wird. Eine Einschnürung im System vergrößert die Fließgeschwindigkeit des Weines. Durch den dabei erzeugten Unterdruck gegenüber der Umgebungsluft wird Luft durch einen Kanal an der engsten Stelle des Ausgusses angesaugt und unter die Flüssigkeit gemischt; es kommt zu einem Druckausgleich mit Blasenbildung. Die hierbei entstehende Vergrößerung der Oberflächen erleichtert die Entfaltung von Geschmacks- und Aromastoffen.

Pflanzenschutz

>Luftinjektordüsen aus dem Pflanzenschutz

Bei Pflanzenschutzgeräten werden Venturi-Düsen eingesetzt, um die Abdrift der Tropfen zu verringern. Hierbei wird der Spritzbrühe Luft beigemischt, um die Tropfen größer werden zu lassen.

Torluftschleier

Luftschleieranlage in einem Verwaltungsgebäude

Bei Luftschleieranlagen kann der Schleier gleichmäßig über die gesamte Breite der Anlage verteilt werden, indem man den Luftstrom durch einen engen Spalt lenkt.

Abgasreinigung

In der Abgasreinigung werden Venturi-Rohre zur gemeinsamen Abscheidung von gas- und partikelförmigen Schadstoffen eingesetzt. In oder kurz vor der Querschnittsverengung wird Waschflüssigkeit zugegeben und durch die hohe Gasgeschwindigkeit vernebelt. Venturiwäscher sind in der Lage, Partikel deutlich kleiner als 1 µm abzuscheiden.

Mathematische Beschreibung

Venturi-Rohr

Aus Bernoulli-Gleichung:

${\frac {w_{1}^{2}\rho }{2}}+p_{1}+\rho gz_{1}={\frac {w_{2}^{2}\rho }{2}}+p_{2}+\rho gz_{2}$

mit

$z_{1}-z_{2}=h$

$p_{1}-p_{2}=\Delta p$

folgt

$\Delta p+\rho gh={\frac {1}{2}}\rho (w_{2}^{2}-w_{1}^{2})={\frac {1}{2}}\rho w_{2}^{2}\left(1-{\frac {w_{1}^{2}}{w_{2}^{2}}}\right)$

Aufgrund der Massenerhaltung nach dem Kontinuitätsgesetz

$w_{1}A_{1}=w_{2}A_{2}$

$w_{1}={\frac {A_{2}}{A_{1}}}w_{2}$

gilt weiterhin

$\Delta p+\rho gh={\frac {1}{2}}\,\rho \,w_{2}^{2}\left(1-\left[{\frac {A_{2}}{A_{1}}}\right]^{2}\right)$

$w_{2}={\sqrt {\frac {2(\Delta p+\rho gh)}{\rho \left(1-\left[{\frac {A_{2}}{A_{1}}}\right]^{2}\right)}}}$

Damit ergibt sich der Massenstrom im Venturi-Rohr zu

${\dot {m}}=\rho A_{2}w_{2}=\rho {\frac {A_{2}}{\sqrt {1-\left({\frac {A_{2}}{A_{1}}}\right)^{2}}}}{\sqrt {{\frac {2}{\rho }}(\Delta p+\rho gh)}}$

Siehe auch

Lavaldüse zur Beschleunigung eines Fluids auf Überschallgeschwindigkeit
Fluiddynamik
Kielsonde

Literatur

Ernst Götsch: Luftfahrzeug-Technik. 4. Auflage. Motorbuch, Stuttgart 2005, ISBN 3-613-02006-8.
Wolfgang Kühr: Technik I. Schiffmann, Bergisch Gladbach 1989, ISBN 3-921270-05-7 (Der Privatflugzeugführer. Band 1).

Basierend auf einem Artikel in:

Wikipedia.de