
Injektive Funktion
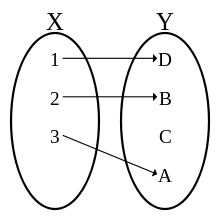
Jedes Element von Y hat höchstens ein Urbild: A, B, D je eines, C keines.
Injektivität oder Linkseindeutigkeit ist eine Eigenschaft einer mathematischen Relation, also insbesondere auch einer Funktion (wofür man meist gleichwertig auch „Abbildung“ sagt): Eine injektive Funktion, auch als Injektion bezeichnet, ist ein Spezialfall einer linkseindeutigen Relation, namentlich der, bei dem die Relation auch rechtseindeutig und linkstotal ist.
Eine Funktion
ist injektiv, wenn es zu jedem Element
der Zielmenge
höchstens ein (also eventuell gar kein) Element
der Ausgangs- oder Definitionsmenge
gibt, das darauf zielt, wenn also nie zwei oder mehr verschiedene
Elemente der Definitionsmenge auf dasselbe Element der Zielmenge abgebildet
werden:
Die Zielmenge kann daher nicht weniger mächtig als die Definitionsmenge sein, d.h., sie kann nicht weniger Elemente enthalten.
Die Bildmenge
darf eine echte Teilmenge
der Zielmenge
sein, d.h., es kann Elemente
geben, die keine Bildelemente
sind, wie es in der abgebildeten Grafik rechts der Fall ist. Dies macht den
Unterschied zu einer bijektiven
Abbildung aus, von der außer Injektivität noch verlangt wird, dass jedes
Element der Zielmenge als Bildelement
auftritt, dass also
surjektiv
ist.
Dass eine Abbildung
injektiv ist, wird gelegentlich durch
ausgedrückt, mit einem aus
und
zusammengesetzten Zeichen. Es erinnert an die Einbettung
einer Menge
in eine Obermenge
durch eine Funktion
die jedes Element von
auf sich selbst abbildet.
Beispiele und Gegenbeispiele
- Außermathematisches Beispiel: Die Funktion, die jedem Bürger der Bundesrepublik Deutschland mit Personalausweis die Nummer seines aktuellen Personalausweises zuordnet, ist injektiv, wobei als Zielmenge die Menge aller möglichen Personalausweisnummern angenommen wird (denn Personalausweisnummern werden nur einmal vergeben).
bezeichne die Menge der natürlichen und
die Menge der ganzen Zahlen.
ist injektiv.
ist injektiv.
ist injektiv.
ist nicht injektiv, da z.B.
gilt.
- Jede Funktion
von einer zweielementigen Menge
in eine einelementige Menge
ist nicht injektiv, weil notwendigerweise beide Elemente von
auf das einzige Element
abgebildet werden:
-
trotz
Eigenschaften
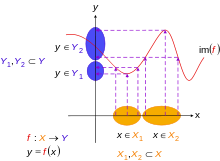
- Man beachte, dass die Injektivität einer Funktion
nur vom Funktionsgraphen
abhängt (im Gegensatz zur Surjektivität, die auch von der Zielmenge
abhängt, die man am Funktionsgraphen nicht ablesen kann).
- Eine Funktion
ist genau dann injektiv, wenn für alle Teilmengen
gilt:
- Eine Funktion
ist genau dann injektiv, wenn
für alle
gilt (wobei
die Urbildfunktion bezeichnet).
- Sind die Funktionen
und
injektiv, dann ist auch die Komposition (Verkettung)
injektiv.
- Aus der Injektivität von
folgt, dass
injektiv ist.
- Eine Funktion
mit nichtleerer Definitionsmenge
ist genau dann injektiv, wenn
eine Linksinverse hat, das ist eine Funktion
mit
(wobei
die identische Abbildung auf
bezeichnet).
- Eine Funktion
ist genau dann injektiv, wenn sie linkskürzbar ist, wenn also für beliebige Funktionen
aus
die Gleichheit
folgt. (Diese Eigenschaft motiviert den in der Kategorientheorie verwendeten Begriff Monomorphismus, jedoch sind bei allgemeinen Morphismen injektiv und linkskürzbar nicht mehr äquivalent.)
- Jede beliebige Funktion
ist als Verkettung
darstellbar, wobei
surjektiv und
injektiv (nämlich eine Inklusionsabbildung) ist.
- Eine stetige
reellwertige
Funktion auf einem reellen Intervall
ist genau dann injektiv, wenn sie in ihrem ganzen Definitionsbereich streng
monoton steigend oder streng monoton fallend ist, d.h., wenn für
zwei beliebige Zahlen
und
aus dem Definitionsbereich gilt: Aus
folgt
(steigend), bzw. aus
folgt
(fallend).
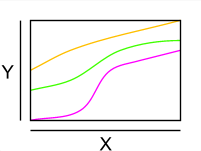
Drei injektive streng monoton steigende reelle
Funktionen. |
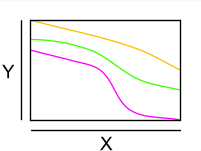
Drei injektive streng monoton fallende reelle
Funktionen. |
- Ein Gruppen- oder Vektorraumhomomorphismus ist genau dann injektiv, wenn sein Kern trivial ist, d.h. nur aus dem neutralen Element bzw. dem Nullvektor besteht.
Mächtigkeiten von Mengen
Eine wichtige Rolle spielt der Begriff der Injektion in der Mengenlehre bei Definition
und Vergleich von Mächtigkeiten,
einem Begriff, der die Elementeanzahl von endlichen Mengen auf beliebige Mengen
verallgemeinert. Zwei Mengen
heißen „von gleicher Mächtigkeit“, wenn es sowohl eine Injektion von
>
nach
als auch eine solche von
nach
gibt. (In diesem Fall existieren auch Bijektionen von der einen auf die andere
Menge.) Dagegen heißt
von kleinerer Mächtigkeit als
,
wenn es zwar eine Injektion von
nach
,
aber keine von
nach
gibt.
Schubfachschluss
Ein in Beweisen insbesondere der Zahlentheorie häufiges Schlussschema benutzt
die Feststellung, dass eine Abbildung
einer endlichen Menge
in eine Menge
mit weniger Elementen nicht injektiv sein kann, dass es also Elemente
mit
und gleichem Bild
gibt. Wegen der Vorstellung von vielen Objekten in weniger Schubfächern heißt
das „Schubfachschluss“.
Anzahl injektiver Abbildungen
Die Anzahl der injektiven Abbildungen von einer Definitionsmenge
in eine gegebene endliche Zielmenge
mit der Eigenschaft
ist gegeben durch:
Dies entspricht in der Kombinatorik einer Variation ohne Wiederholung.
Geschichte
Nachdem man generationenlang mit Formulierungen wie „eineindeutig“ ausgekommen war, kam erst in der Mitte des 20. Jahrhunderts mit der durchgehend mengentheoretischen Darstellung aller mathematischen Teilgebiete das Bedürfnis nach einer prägnanteren Bezeichnung auf.
Im Englischen lässt sich das Substantiv injection 1945 belegen. Das englische Adjektiv injective wurde 1952 in den Foundations of algebraic topology von S. Eilenberg und N. Steenrod verwendet, allerdings eher im Sinne von injektiven Objekten. Injektiv im Kontext mit den Fachwörtern surjektiv und bijektiv wurde 1954 von der Autorengruppe Nicolas Bourbaki in dem Buch Théorie des ensembles, Éléments de mathématique Première Partie eingeführt.
Es herrscht stellenweise große Verwirrung bezüglich der Zuordnung zwischen den Begriffen „eineindeutig“ einerseits und „injektiv“ bzw. „bijektiv“ andererseits. Quellen (Lehrbücher) aus der reinen Mathematik favorisieren „injektiv“, fachfremde Quellen favorisieren teilweise eher „bijektiv“.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 05.02. 2021