Körper (Algebra)
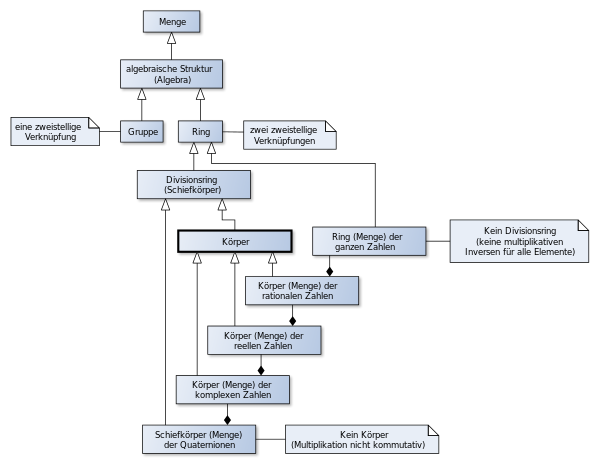
Ein Körper ist im mathematischen Teilgebiet der Algebra eine ausgezeichnete algebraische Struktur, in der die Addition, Subtraktion, Multiplikation und Division auf eine bestimmte Weise durchgeführt werden können.
Die Bezeichnung „Körper“ wurde im 19. Jahrhundert von Richard Dedekind eingeführt.
Die wichtigsten Körper, die in fast allen Gebieten der Mathematik benutzt
werden, sind der Körper
der rationalen
Zahlen, der Körper
der reellen Zahlen und der
Körper
der komplexen Zahlen.
Formale Definition
Allgemeine Definition
Ein Körper ist eine Menge ,
versehen mit zwei inneren
zweistelligen Verknüpfungen „
“
und „
“
(die Addition und Multiplikation genannt werden), für die folgende
Bedingungen erfüllt sind:
ist eine abelsche Gruppe (neutrales Element 0).
ist eine abelsche Gruppe (neutrales Element 1).
- Distributivgesetze:
für alle
.
für alle
.
Einzelaufzählung der benötigten Axiome
Ein Körper muss also folgende Einzelaxiome erfüllen:
- Additive Eigenschaften:
für alle
(Assoziativgesetz)
für alle
(Kommutativgesetz)
- Es gibt ein Element
, sodass
für alle
(neutrales Element).
- Zu jedem
existiert ein additives Inverse
mit
.
- Multiplikative Eigenschaften:
für alle
(Assoziativgesetz)
für alle
(Kommutativgesetz)
- Es gibt ein Element
, sodass
für alle
(neutrales Element).
- Zu jedem
existiert ein multiplikatives Inverse
mit
.
- Zusammenspiel von additiver und multiplikativer Struktur:
für alle
(Links-Distributivgesetz)
für alle
(Rechts-Distributivgesetz)
Definition als spezieller Ring
Ein kommutativer unitärer Ring, der nicht der Nullring ist, ist ein Körper, wenn in ihm jedes von Null verschiedene Element ein Inverses bezüglich der Multiplikation besitzt.
Anders formuliert, ist ein Körper ein kommutativer unitärer Ring ,
in dem die Einheitengruppe
gleich
ist.
Bemerkungen
Die Definition sorgt dafür, dass in einem Körper in der „gewohnten“ Weise Addition, Subtraktion und Multiplikation funktionieren sowie die Division mit Ausnahme der nicht lösbaren Division durch 0:
- Das Inverse von
bezüglich der Addition ist
und wird meist das additiv Inverse zu
oder auch das Negative von
genannt.
- Das Inverse von
bezüglich der Multiplikation ist
und wird das (multiplikativ) Inverse zu oder der Kehrwert von
genannt.
ist das einzige Element des Körpers, das keinen Kehrwert hat, die multiplikative Gruppe eines Körpers ist also
.[1]
Anmerkung: Die Bildung des Negativen eines Elementes hat nichts mit
der Frage zu tun, ob das Element selbst negativ ist; beispielsweise ist das
Negative der reellen Zahl
die positive Zahl
.
In einem allgemeinen Körper gibt es keinen Begriff von negativen oder positiven
Elementen. (Siehe auch geordneter
Körper.)
Verallgemeinerungen: Schiefkörper und Koordinatenkörper
Verzichtet man auf die Bedingung, dass die Multiplikation kommutativ ist, so gelangt man zur Struktur des Schiefkörpers. Es gibt jedoch auch Autoren, die für einen Schiefkörper explizit voraussetzen, dass die Multiplikation nicht kommutativ ist. In diesem Fall ist ein Körper nicht mehr zugleich Schiefkörper. Ein Beispiel ist der Schiefkörper der Quaternionen, der kein Körper ist. Andererseits gibt es Autoren, so Nicolas Bourbaki, die Schiefkörper als Körper und die hier besprochenen Körper als kommutative Körper bezeichnen.
In der analytischen Geometrie werden Körper zur Koordinatendarstellung von Punkten in affinen und projektiven Räumen verwendet, siehe Affine Koordinaten, Projektives Koordinatensystem. In der synthetischen Geometrie, in der auch Räume (insbesondere Ebenen) mit schwächeren Eigenschaften untersucht werden, benutzt man als Koordinatenbereiche („Koordinatenkörper“) auch Verallgemeinerungen der Schiefkörper, nämlich Alternativkörper, Quasikörper und Ternärkörper.
Eigenschaften und Begriffe
- Es gibt genau eine „0“ (Null-Element, neutrales Element bzgl. der Körper-Addition) und eine „1“ (Eins-Element, neutrales Element bzgl. der Körper-Multiplikation) in einem Körper.
- Jeder Körper ist ein Ring. Die Eigenschaften der multiplikativen Gruppe heben den Körper aus den Ringen heraus. Wenn die Kommutativität der multiplikativen Gruppe nicht gefordert wird, erhält man den Begriff des Schiefkörpers.
- Jeder Körper ist nullteilerfrei: Ein Produkt zweier Elemente des Körpers ist genau dann 0, wenn mindestens einer der Faktoren 0 ist.
- Jedem Körper lässt sich eine Charakteristik zuordnen, die entweder 0 oder eine Primzahl ist.
- Die kleinste Teilmenge eines Körpers, die selbst noch alle Körperaxiome
erfüllt, ist sein Primkörper.
Der Primkörper ist entweder isomorph zum Körper
der rationalen Zahlen (bei Körpern der Charakteristik 0) oder ein endlicher Restklassenkörper
(bei Körpern der Charakteristik
, speziell bei allen endlichen Körpern, s.u.).
- Ein Körper ist ein eindimensionaler Vektorraum über sich selbst als zugrundeliegendem Skalarkörper. Darüber hinaus existieren über allen Körpern Vektorräume beliebiger Dimension. (→ Hauptartikel Vektorraum).
- Ein wichtiges Mittel, um einen Körper
algebraisch zu untersuchen, ist der Polynomring
der Polynome in einer Variablen mit Koeffizienten aus
.
- Man nennt einen Körper
algebraisch abgeschlossen, wenn sich jedes nichtkonstante Polynom aus
in Linearfaktoren aus
zerlegen lässt.
- Man nennt einen Körper
vollkommen, wenn kein irreduzibles nichtkonstantes Polynom aus
in irgendeiner Körpererweiterung mehrfache Nullstellen hat. Algebraische Abgeschlossenheit impliziert Vollkommenheit, aber nicht umgekehrt.
- Man nennt einen Körper
- Wenn in einem Körper eine Totalordnung
definiert ist, die mit der Addition und der Multiplikation verträglich ist,
spricht man von einem geordneten
Körper und nennt die Totalordnung auch Anordnung des Körpers.
In solchen Körpern kann man von negativen und positiven Zahlen sprechen.
- Wenn in dieser Anordnung jedes Körperelement
durch eine endliche Summe des Einselementes übertroffen werden kann (
), sagt man, der Körper erfüllt das Archimedische Axiom oder auch, er ist archimedisch geordnet.
- Wenn in dieser Anordnung jedes Körperelement
- In der Bewertungstheorie werden bestimmte Körper mit Hilfe einer Bewertungsfunktion untersucht. Man nennt sie dann bewertete Körper.
- Ein Körper
besitzt als Ring nur die trivialen Ideale
und
.
- Jeder nicht-konstante Homomorphismus von einem Körper in einen Ring ist injektiv.
Körpererweiterung
Eine Teilmenge
eines Körpers
,
die selbst mit dessen Operationen wieder einen Körper bildet, wird Unter- oder
Teilkörper genannt. Das Paar
und
heißt Körpererweiterung
,
oder
.
Beispielsweise ist der Körper der rationalen Zahlen
ein Teilkörper der reellen Zahlen
.
Eine Teilmenge
eines Körpers
ist ein Teilkörper, wenn sie folgende Eigenschaften hat:
,
(Abgeschlossenheit bezüglich Addition und Multiplikation)
(Zu jedem Element aus
ist auch das additive Inverse in
.)
(Zu jedem Element aus
mit Ausnahme der Null ist auch das multiplikativ Inverse in
.)
Das algebraische Teilgebiet, das sich mit der Untersuchung von Körpererweiterungen beschäftigt, ist die Galoistheorie.
Beispiele
- Bekannte Beispiele für Körper sind
- der Körper der rationalen
Zahlen
, d. h. die Menge der rationalen Zahlen mit der üblichen Addition und Multiplikation
- der Körper der reellen
Zahlen
, d. h. die Menge der reellen Zahlen mit der üblichen Addition und Multiplikation, und
- der Körper der komplexen
Zahlen
d. h. die Menge der komplexen Zahlen mit der üblichen Addition und Multiplikation.
- der Körper der rationalen
Zahlen
- Körper können durch Adjunktion
erweitert werden. Ein wichtiger Spezialfall – insbesondere in der Galoistheorie – sind algebraische
Körpererweiterungen des Körpers
. Der Erweiterungskörper kann dabei als Vektorraum über
aufgefasst werden.
ist ein Körper. Es genügt zu zeigen, dass das Inverse von
auch von der angegebenen Form ist:
Eine mögliche Basis vonist {
}.
ist ein Körper mit Basis {
}.
- Weitere Beispiele liefern die Restklassenkörper
mit
Primzahl und
- deren endliche Körpererweiterungen, die endlichen Körper,
- allgemeiner deren algebraische Körpererweiterungen, die Frobeniuskörper, und
- noch allgemeiner deren beliebige Körpererweiterungen, die Körper mit Primzahlcharakteristik.
- Zu jeder Primzahl
der Körper
der p-adischen Zahlen.
- Die Menge der ganzen Zahlen
mit den üblichen Verknüpfungen ist kein Körper: Zwar ist
eine Gruppe mit neutralem Element
und jedes
besitzt das additive Inverse
, aber
ist keine Gruppe. Immerhin ist
das neutrale Element, aber außer zu
und
gibt es keine multiplikativen Inversen (zum Beispiel ist
keine ganze, sondern eine echt rationale Zahl):
- Die ganzen Zahlen bilden lediglich einen Integritätsring, dessen Quotientenkörper die rationalen Zahlen sind.
- Das Konzept, mit dem sich der Integritätsring der ganzen Zahlen zum Körper
der rationalen Zahlen erweitern und in diesen einbetten lässt, kann auf
beliebige Integritätsringe verallgemeinert werden:
- So entsteht in der Funktionentheorie aus dem Integritätsring der auf einem Gebiet der komplexen Zahlenebene holomorphen Funktionen der Körper, der auf demselben Gebiet meromorphen Funktionen und abstrakter
- aus dem Integritätsring der formalen Potenzreihen
über einem Körper
dessen Quotientenkörper, analog aus dem Integritätsring der formalen Dirichletreihen
- aus dem Ring der Polynome
in
Variablen,
, dessen Quotientenkörper, der Körper der rationalen Funktionen
in ebenso vielen Variablen.
Endliche Körper
| + | O | I | A | B |
|---|---|---|---|---|
| O | O | I | A | B |
| I | I | O | B | A |
| A | A | B | O | I |
| B | B | A | I | O |
| · | O | I | A | B |
|---|---|---|---|---|
| O | O | O | O | O |
| I | O | I | A | B |
| A | O | A | B | I |
| B | O | B | I | A |
Ein Körper ist ein endlicher Körper, wenn seine Grundmenge
endlich ist. Die endlichen Körper sind in folgendem Sinne vollständig
klassifiziert: Jeder endliche Körper hat genau
Elemente mit einer Primzahl
und einer positiven natürlichen
Zahl
.
Bis auf Isomorphie
gibt es zu jedem solchen
genau einen endlichen Körper, der mit
bezeichnet wird. Jeder Körper
hat die Charakteristik
.
Als Beispiel werden hier die Additions- und Multiplikationstafeln des
gezeigt; farbig hervorgehoben dessen Unterkörper
.
Im Spezialfall
erhalten wir zu jeder Primzahl
den Körper
,
der isomorph zum Restklassenkörper
ist. Für
ist
niemals isomorph zu
;
stattdessen ist
isomorph zu
,
wobei
den Ring der Polynome mit Koeffizienten in
darstellt (hier ist
)
und
ein normiertes
irreduzibles
Polynom vom Grad
ist. In
ist ein normiertes Polynom irreduzibel, wenn aus
folgt, dass
oder
ein Element von
ist, also ein konstantes Polynom. Hier bedeutet
das von
erzeugte
Ideal.
Geschichte
Wesentliche Ergebnisse der Körpertheorie sind Évariste Galois und Ernst Steinitz zu verdanken.
Siehe auch
Literatur
- Siegfried Bosch: Algebra. 7. Auflage. Springer-Verlag, 2009, ISBN 3-540-40388-4.
- Thomas W. Hungerford: Algebra. 5. Auflage. Springer-Verlag, 1989, ISBN 0-387-90518-9.
Anmerkungen
- ↑
Jegliche Lösung
jeder Gleichung
verletzt die Ringaxiome.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 16.01. 2021