Leitungsgleichung

Unter Leitungsgleichung oder Leitungsgleichungen (kurz für Telegraphenleitungsgleichung bzw. Telegraphenleitungsgleichungen, alternativ Telegrafengleichung bzw. Telegrafengleichungen) versteht man in der Elektrotechnik ein System gekoppelter partieller Differentialgleichungen erster Ordnung, das die Ausbreitung von Strom und Spannung auf einer langen, geraden, zweiadrigen (zweipoligen) Leitung beschreibt.

Die Leitungstheorie beschäftigt sich mit der Analyse von Leitungen, indem sie diese Leitungsgleichungen mit verschiedenen, den jeweiligen Randbedingungen angepassten mathematischen Methoden löst.

Allgemeines

Bringt man stromführende Leitungen (im Folgenden als „Adern“ bezeichnet) in räumliche Nähe zueinander, fasst sie sogar in einem Kabel zusammen, oder hat eine Leitung einen hinreichend großen Querschnitt, so zeigen sich Effekte, die bei dünnen, räumlich voneinander getrennten Leitungen vernachlässigbar klein sind:

Die Adern bilden Kapazitäten gegeneinander aus (vgl. die Analogie zum Plattenkondensator).
Sie zeigen induktive Eigenschaften.
Sind die Adern nicht ideal gegeneinander isoliert, treten Querleitverluste auf, also ein (i.d.R. unerwünschter) Stromfluss zwischen den Adern.

Mit Hilfe der Telegrafengleichungen lassen sich zweiadrige Leitungen beschreiben, also Kabel, die zwei stromführende „Drähte“ aufweisen. Der einfachste Fall einer solchen Leitung ist die sogenannte Lecher-Leitung. Hierbei handelt es sich um zwei parallele Drähte endlicher Dicke, die – gegeneinander isoliert – in einem Kabel geführt werden und später als Telegrafenleitungen Verwendung fanden. In der Technik finden auch kompliziertere Leitungen als die Lecher-Leitung Verwendung, wie etwa die Koaxialleitung, die bei vielen Hochfrequenzanwendungen und in der modernen Messelektronik eine große Rolle spielen. Eine Ader der Koaxialleitung ist ein Hohlzylinder (die sogenannte äußere Ader), entlang dessen Achse die zweite, ebenfalls zylinderförmige und durch einen Isolator von der äußeren Leitung getrennte innere Ader (auch „Seele“) geführt wird.

Historisch gesehen wurde die Leitungsgleichung maßgeblich von Oliver Heaviside für die Analyse von Problemen mit langen Telegrafenleitungen, die unter Wasser verlegt wurden, entwickelt. Es mag zunächst erstaunen, dass diese Leitungen über nur ein stromführendes Kabel, also im Prinzip nur über eine Ader, verfügten. Da als Rückleiter jedoch das Meerwasser diente, lässt sich das System Ozean-Kabel als eine Leitung mit zwei Adern auffassen und mit der hier thematisierten Telegrafenleitungsgleichung beschreiben.

Das Gleichungssystem im Detail

Allgemeine Form und charakteristische Größen

Im Falle einer hinreichend geraden Leitung, die sich in -Richtung erstreckt, ist das System der Telegrafengleichungen durch

${\begin{alignedat}{2}{\frac {\partial U(x,t)}{\partial x}}&=-L'(x){\frac {\partial I(x,t)}{\partial t}}&&\,-R'(x)I(x,t)\\{\frac {\partial I(x,t)}{\partial x}}&=-G'(x)U(x,t)&&\,-C'(x){\frac {\partial U(x,t)}{\partial t}}\end{alignedat}}$

gegeben. Die Funktionen , , und sind im Allgemeinen Funktionen des Ortes. Für den Normalfall der homogenen Leitungen sind sie ortsunabhängig und damit charakteristische Konstanten der Leitung, die Leitungsbeläge (auch als „primäre Leitungskonstanten“ bezeichnet):

R' heißt Widerstandsbelag und gibt den ohmschen Widerstand der Leitung pro Längeneinheit an.
C' heißt Kapazitätsbelag und gibt die Kapazität der Leitung pro Längeneinheit an.
L' heißt Induktivitätsbelag und gibt die Induktivität der Leitung pro Längeneinheit an.
G' heißt Ableitungsbelag und gibt den Leitwert pro Längeneinheit zwischen den beiden stromführenden Adern an.

Motivation der Gleichungen

Abbildung 1: Das zweite Argument der Funktionen U und I, die Zeit t, wurde in der Darstellung der Übersicht halber unterdrückt

Die Telegrafengleichungen lassen sich aus den elementaren Gesetzen der Elektrotechnik, nämlich der Knoten- und der Maschenregel, herleiten, wenn man sich die gesamte Leitung aus kleineren Einheiten der Länge $\Delta x$ mit einer inneren Schaltungsstruktur aufgebaut denkt. 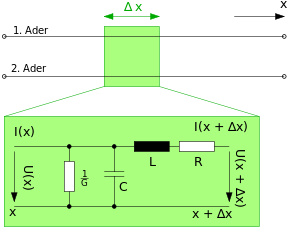Da die Herleitung aus mathematischer Sicht allerdings nicht als streng zu bezeichnen ist, ist dieser Abschnitt mit „Motivation der Gleichung“ und nicht mit „Herleitung“ überschrieben. Der „innere“ Aufbau eines solchen Leitungssegmentes ist in Abbildung 1 dargestellt: Die Kapazität des Leitungsstücks wird durch einen Kondensator der Kapazität $C=C'(x)\Delta x$ zusammengefasst, sein ohmscher Widerstand in einem einzelnen ohmschen Bauelement mit dem Widerstandswert $R=R'(x)\Delta x$ , seine Induktivität entsprechend mit einer Spule der Selbstinduktivität $L=L'(x)\Delta x$ . Querleitverluste werden durch einen Querwiderstand zwischen den beiden Adern modelliert. Dieser ohmsche Widerstand mit (meist sehr geringem) Leitwert $G=G'(x)\Delta x$ steht für den Isolator, der die Adern der Leitung voneinander trennt. Wendet man die Maschenregel auf diejenige Masche an, die nur die Spannung U(x,t) , die Spule, den ohmschen Widerstand und die Spannung $U(x+\Delta x,t)$ enthält, so erhalten wir unter Beachtung der Vorzeichen:

$U(x+\Delta x,t)-U(x,t)+RI(x+\Delta x,t)+L{\frac {\partial I(x+\Delta x,t)}{\partial t}}=0.$

Setzen wir nun $L=L'(x)\Delta x$ sowie $R=R'(x)\Delta x$ in die Gleichung ein, so sehen wir:

$U(x+\Delta x,t)-U(x,t)=-R'\Delta xI(x+\Delta x,t)-L'\Delta x{\frac {\partial I(x+\Delta x,t)}{\partial t}},$

Ist $\Delta x$ hinreichend klein, so gilt:

$U(x+\Delta x,t)=U(x,t)+{\frac {\partial U(x,t)}{\partial x}}\Delta x$

und es ergibt sich:

${\frac {\partial U(x,t)}{\partial x}}\Delta x=-R'\Delta xI(x+\Delta x,t)-L'\Delta x{\frac {\partial I(x+\Delta x,t)}{\partial t}}.$

Wir dividieren durch $\Delta x$ und bekommen:

${\frac {\partial U(x,t)}{\partial x}}=-R'I(x+\Delta x,t)-L'{\frac {\partial I(x+\Delta x,t)}{\partial t}}.$

Nun gilt außerdem:

$I(x+\Delta x,t)=I(x,t)+{\frac {\partial I(x,t)}{\partial x}}\Delta x$

sowie

${\frac {\partial I(x+\Delta x,t)}{\partial t}}={\frac {\partial I}{\partial t}}(x,t)+{\frac {\partial ^{2}I(x,t)}{\partial x\partial t}}\Delta x$

Für kleine $\Delta x$ , also für $\Delta x\rightarrow 0$ , gehen diese Ausdrücke über in I(x,t) bzw. $\partial I(x,t)/\partial t$ . Einsetzen liefert die Gleichung:

${\frac {\partial U(x,t)}{\partial x}}=-R'I(x,t)-L'{\frac {\partial I(x,t)}{\partial t}},$

was die erste der beiden Telegrafengleichungen darstellt. Aus der Knotenregel erhalten wir die Gleichung

$I(x+\Delta x,t)=I(x,t)-GU(x,t)-C{\frac {\partial U(x,t)}{\partial t}}.$

Einsetzen von

$I(x+\Delta x,t)=I(x,t)+{\frac {\partial I(x,t)}{\partial x}}\Delta x$

sowie

$G=G'(x)\Delta x$ und $C=C'(x)\Delta x$ liefert nach anschließender Division durch $\Delta x$ die zweite Telegrafengleichung:

${\frac {\partial I(x,t)}{\partial x}}=-G'U(x,t)-C'{\frac {\partial U(x,t)}{\partial t}}.$

Die Konsistenz des Modells könnte man durch die beiden Querleitverbindungen gefährdet sehen, da es reine Willkür ist, an welcher Stelle der Schaltung sie in das Modell eines „Leitungssegmentes“ einzubringen sind. Schließlich stellen diese Verbindungen letztlich Zusammenfassungen von Prozessen dar, die an sich kontinuierlicher Natur sind. So könnten wir die Querleitverbindung, die den Kondensator enthält, auch zwischen den ohmschen Widerstand und die Spule schalten. Da die Herleitung aber nicht von der konkreten Position der Querverbindungen abhängt (für die Knotenregel ist allein die Existenz der Verbindungen notwendig, die Maschenregel wurde auf eine Masche angewandt, die die beiden Querverbindungen nicht enthält), ist das Modell in diesem Sinne selbstkonsistent.

Entkopplung des Systems

Im Falle konstanter Beläge lässt sich das System der Telegrafengleichungen entkoppeln. Dazu ist die erste Gleichung einmal partiell nach dem Ort abzuleiten, die zweite Gleichung nach der Zeit . Die dadurch entstandene zweite Gleichung lässt sich wegen der Vertauschbarkeit partieller Ableitungen in die erste einsetzen, und man erhält für Strom und Spannung jeweils eine eigene Differenzialgleichung:

${\frac {\partial ^{2}U(x,t)}{\partial x^{2}}}-L'C'{\frac {\partial ^{2}U(x,t)}{\partial t^{2}}}=(L'G'+R'C'){\frac {\partial U(x,t)}{\partial t}}+R'G'U(x,t)$

und

${\frac {\partial ^{2}I(x,t)}{\partial x^{2}}}-L'C'{\frac {\partial ^{2}I(x,t)}{\partial t^{2}}}=(L'G'+R'C'){\frac {\partial I(x,t)}{\partial t}}+R'G'I(x,t)$

Man beachte allerdings, dass diese beiden Gleichungen nicht mehr äquivalent zu dem Ausgangssystem sind, da die Bildung der partiellen Ableitung keine Äquivalenzumformung darstellt. Zwar ist jede Lösung der Telegrafengleichung auch Lösung der entkoppelten Gleichungen, aber nicht jede Lösung der entkoppelten Gleichungen muss auch eine Lösung der Telegrafengleichung sein. Dennoch kann man aus den entkoppelten Gleichungen Informationen gewinnen: Bei den entkoppelten Gleichungen handelt es sich um Wellengleichungen. Da sich die Lösungen der Telegrafengleichung aber unter denen der entkoppelten Gleichungen befinden, erwarten wir also wellenförmige Spannungs- und Stromverläufe als Lösungen der Telegrafengleichung.

Lösung der Telegrafengleichung

Im Falle konstanter Beläge und dem Betrieb der Leitung mit stationären sinusförmigen Signalen lässt sich die Telegrafengleichung durch den Ansatz ebener Wellen lösen:

${\begin{aligned}U(x,t)&=u_{0}e^{{j\omega t-\gamma x}}\\I(x,t)&=i_{0}e^{{j\Omega t-\Gamma x}}\end{aligned}}$

Dabei lassen wir zu, dass $\gamma$ und $\Gamma$ komplexe Zahlen sind. Setzt man diese ebenen Wellen in die Telegrafengleichung ein sieht man, dass die Lösungen nur dann für beliebige Zeiten gelten können, wenn $\omega =\Omega$ gilt. Ebenso kann die Lösung nur dann für beliebige gelten, wenn $\gamma =\Gamma$ ist.

Weiterhin findet man durch Einsetzen des Ansatzes in die Telegrafengleichung, dass die Amplituden u_0 und $i_{0}$ Lösung des linearen homogenen Gleichungssystems

${\begin{aligned}-\gamma u_{0}+(L'j\omega +R')i_{0}&=0\\(C'j\omega +G')u_{0}-\gamma i_{0}&=0\end{aligned}}$

sind. Dieses besitzt aber nur dann nicht-triviale Lösungen, wenn die Determinante der Koeffizientenmatrix verschwindet:

$\det {\begin{pmatrix}-\gamma &L'j\omega +R'\\C'j\omega +G'&-\gamma \end{pmatrix}}=0,$

was genau dann der Fall ist, wenn $\gamma$ der Gleichung

$\gamma ^{2}=(R'+j\omega L')(G'+j\omega C')\Leftrightarrow \gamma =\pm {\sqrt {(R'+j\omega L')(G'+j\omega C')}}$

genügt. Da die Telegrafengleichung linear ist, ist die Summe zweier Lösungen wieder eine Lösung (Superpositionsprinzip), so dass wir als allgemeinste Lösung, die wir aus dem Ansatz ebener Wellen gewinnen können, festhalten:

${\begin{aligned}U(x,t)&=u_{1}e^{{j\omega t-\gamma x}}+u_{2}e^{{j\omega t+\gamma x}}\\I(x,t)&=i_{1}e^{{j\omega t-\gamma x}}+i_{2}e^{{j\omega t+\gamma x}}\end{aligned}}$

mit $\gamma ={\sqrt {(R'+j\omega L')(G'+j\omega C')}}$ . $\gamma$ heißt auch (komplexe) Übertragungskonstante oder Fortpflanzungskonstante.

Wellenwiderstand und Reflektivität

Im Falle konstanter Beläge und einer verlustfreien Leitung (d.h. R'=0 , G'=0 ) lässt sich durch Einsetzen zeigen, dass eine Spannung der Form

$U(x,t)=u_{1}e^{{j\omega t-\gamma x}}+u_{2}e^{{j\omega t+\gamma x}}$

stets einen Strom der Form

$I(x,t)={\frac {u_{1}}{Z_{0}}}e^{{j\omega t-\gamma x}}-{\frac {u_{2}}{Z_{0}}}e^{{j\omega t+\gamma x}}$

mit

$Z_{0}={\sqrt {{\frac {L'}{C'}}}}.$

zur Folge hat. Da der Scheitelwert des Stroms $i_{0}$ und der der Spannung u_0 , gegeben durch

${\begin{aligned}u_{0}&={\sqrt {u_{1}^{2}+u_{2}^{2}}}\\i_{0}&={\sqrt {\left({\frac {u_{1}}{Z_{0}}}\right)^{2}+\left({\frac {u_{2}}{Z_{0}}}\right)^{2}}},\end{aligned}}$

über die Beziehung

${\frac {u_{0}}{i_{0}}}=Z_{0}$

verbunden sind, die sehr an das ohmsche Gesetz erinnert, nennt man $Z_{0}$ den Wellenwiderstand der Leitung. Um den Begriff der Reflektivität zu verstehen, betrachten wir noch einmal die obige Darstellung des Spannungsverlaufs. Da die Leitung verlustfrei ist, vereinfacht sich die komplexe Übertragungskonstante zu $\gamma =j\omega {\sqrt {L'C'}}$ , der

Abbildung 2: Leitung, mit komplexen Widerstand abgeschlossen.

Spannungsverlauf ist also eine Überlagerung zweier ebener Wellen, und zwar einer Welle mit Wellenvektor $k_{1}=+\omega {\sqrt {L'C'}}$ (im Folgenden „hinlaufende Welle“ genannt) und einer Welle mit Wellenvektor $k_{2}=-\omega {\sqrt {L'C'}}$ („rücklaufende Welle“). Die erste dieser beiden Wellen läuft in -Richtung, die zweite Welle gegen die -Richtung. Führt man den Anteil der rücklaufenden Welle in der Gesamtwelle auf die Reflexion eines Teiles der hinlaufenden Welle am Ende der Leitung zurück, so gibt das Verhältnis

$r={\frac {u_{2}}{u_{1}}}$

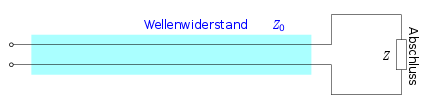
gerade den Bruchteil der einlaufenden Welle an, der am Ende der Leitung reflektiert wurde. Man nennt daher die Reflektivität der Leitung. Man beachte dabei, dass $u_{1}$ die Amplitude der Welle mit Wellenvektor $+\omega {\sqrt {L'C'}}$ , also die Amplitude der hinlaufenden Welle ist und $u_{2}$ die Amplitude der Welle mit Wellenvektor $-\omega {\sqrt {L'C'}}$ , also der rücklaufenden Welle darstellt. Man kann nun zeigen, dass die Reflektivität einer mit einem komplexen Widerstand abgeschlossenen Leitung (Abbildung 2) über

$r={\frac {Z-Z_{0}}{Z+Z_{0}}}$

berechnet werden kann. Den Grenzfall einer offenen Leitung erhalten wir aus der Auswertung des Grenzwertes von für $\left|Z\right|\rightarrow \infty$ : Es ergibt sich r=1 , die gesamte Welle wird also (ohne Phasensprung) reflektiert. Die kurzgeschlossene Leitung entspricht dem Fall Z=0 . Hier ergibt sich eine Reflektivität von −1, die gesamte Welle wird also reflektiert, es findet aber ein Phasensprung um 180° statt.

Basierend auf einem Artikel in:

Wikipedia.de