Daubechies-Wavelets

Unter Daubechies-Wavelets, benannt nach Ingrid Daubechies, versteht man in der digitalen Signalverarbeitung eine Klasse orthogonaler Wavelet-Funktionen, die einen kompakten Träger haben. Sie gehören zu den am häufigsten praktisch eingesetzten Wavelets, die bei Wavelet-Transformationen zum Beispiel für Zwecke der digitalen Signalanalyse und Signalkompression Verwendung finden. Aufgrund ihrer einfachen Implementierbarkeit mittels der schnellen Wavelet-Transformation (FWT) sind sie auch Lehr(buch)beispiele der digitalen Signalverarbeitung.

Beschreibung

Im Sinne der Funktionalanalysis erzeugt die Waveletfunktion zusammen mit ihren ganzzahligen Verschiebungen und den Stauchungen/Streckungen dieser Funktionen mit Zweierpotenzen als Faktor eine Orthonormalbasis des Hilbertraums L²(IR), d.h., jede quadratintegrierbare Funktion kann in Teile zerlegt werden, die der Waveletfunktion ähnlich sehen. Seit 1909 war das Haar-Wavelet, eine stückweise konstante Funktion, mit dieser Eigenschaft bekannt. Es ist das Verdienst von Ingrid Daubechies, als erste eine stetige Funktion mit dieser Eigenschaft konstruiert zu haben.

Zu jedem Wavelet gibt es zwei endliche Folgen reeller Zahlen, welche als digitale Tief- und Hochpassfilter in einer Filterbank, die Teil der FWT ist, eingesetzt werden können. Die Länge N dieser Filter, auch als Anzahl der Taps bezeichnet, ist Teil der Bezeichnung DN der einzelnen Daubechies-Wavelets. In der Praxis werden meist die Daubechies-Wavelets mit den Bezeichnungen D2-D20 verwendet. Aus theoretischen Gründen kommen nur gerade N=2A vor. Jedes Wavelet dieser Klasse hat die maximale Anzahl A verschwindender Momente (in der engl. Literatur „vanishing moments“), d.h., die Waveletfunktion steht senkrecht (im Sinne von L²(IR), d.h. das Integral des Produkts beider Funktionen ist Null) zu jedem Polynom mit Grad höchstens A−1. Beispielsweise hat D2 (das Haar-Wavelet) ein verschwindendes Moment und ist senkrecht zu allen konstanten Funktionen, D4 hat zwei solcher Momente und ist senkrecht zu allen linearen Funktionen (was die konstanten Funktionen einschließt) usw. Die Anzahl A der verschwindenden Momente ist ein Maß der Güte einer Skalierungsfunktion.

Von Ingrid Daubechies wurde ebenfalls eine Klasse biorthogonaler Wavelets mit ähnlicher Charakteristik eingeführt. Diese Wavelets sind nicht mehr orthogonal, aber dafür symmetrisch.

Die orthogonalen Daubechies-Wavelets
	A=2, N=4, Träger [0,3]	A=6, N=12, Träger [0,11]	A=10, N=20, Träger [0,19]
Skalierungs- und Wavelet-Funktionen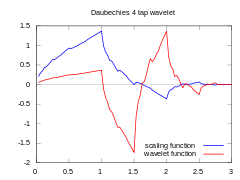
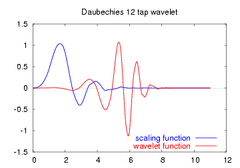Amplituden ihres Frequenzspektrums

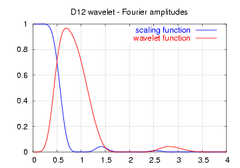Algebraische Bedingungen

Die Skalierungsfunktion in einer jeden Multiskalenanalyse ist Lösung einer fraktalen Funktionalgleichung, die Verfeinerungsgleichung oder Zweiskalengleichung genannt wird:

$\phi (x)=\sum _{{k=0}}^{{N-1}}a_{k}\phi (2x-k)$ ,

wobei die endliche Folge $(a_{0},\dots ,a_{{N-1}})$ reeller Zahlen Skalierungsfolge oder -maske genannt wird. Die Waveletfunktion ergibt sich auf ähnlichem Wege als Linearkombination

$\psi (x)=\sum _{{k=0}}^{{M-1}}b_{k}\phi (2x-k)$ ,

mit einer geeigneten endlichen Folge $(b_{0},\dots ,b_{{M-1}})$ reeller Zahlen, die Waveletfolge oder -maske genannt wird.

Ist die Existenz einer stetigen Lösung der Verfeinerungsgleichung bekannt, so kann eine beliebig genaue Approximation dieser gefunden werden, indem man das endlichdimensionale lineare Gleichungssystem aufstellt, welches die Werte der Skalierungsfunktion an ganzzahligen Stellen erfüllen muss. Da dieses Gleichungssystem homogen ist, fügt man die Bedingung hinzu, dass die Summe dieser Werte 1 sein soll. Aus den Werten an den ganzzahligen Stellen lassen sich dann die Werte zu den Vielfachen von 1/2, aus diesen die Werte zu den Vielfachen von 1/4 etc. durch einfaches Einsetzen finden. Desgleichen gilt für die Werte der Waveletfunktion. Auf diese Weise wurden obige Diagramme erzeugt.

Orthogonale Wavelets

Diese Klasse von Wavelets hat die Eigenschaft, dass die Skalierungsfunktion mitsamt ihren ganzzahligen Verschiebungen im Verein mit der Waveletfunktion mit ihren ganzzahligen Verschiebungen ein Orthonormalsystem im Hilbertraum L²(IR) bilden. Notwendig für diese Orthogonalität ist, dass die Skalierungsfolge senkrecht zu allen geradzahligen Verschiebungen ihrer selbst steht:

$\sum _{{n\in \mathbb{Z } }}a_{n}a_{{n+2m}}=2\delta _{{m,0}}$ .

Im orthogonalen Fall ergeben sich die Koeffizienten der Waveletfolge direkt aus den Koeffizienten der Skalierungsfolge nach

$b_{n}=(-1)^{n}a_{{N-1-n}}\qquad {\text{mit }}n=0,\ldots ,N-1$

Manchmal findet man auch das andere Vorzeichen in der Literatur.

Biorthogonale Wavelets

Die zweite von Ingrid Daubechies zusammen mit Albert Cohen und Jean-Christophe Feauveau eingeführte Klasse sind die biorthogonalen Wavelets. Diese haben zwar nicht die oben genannte Orthogonalitätseigenschaft, weichen von dieser aber nur gering ab. Dafür können sie so konstruiert werden, dass die Skalierungsfunktion symmetrisch und die Waveletfunktion ebenfalls symmetrisch oder antisymmetrisch ist. Jedoch genügt hier nicht ein Paar erzeugender Funktionen, sondern es braucht zwei Skalierungsfunktionen $\phi ,{\tilde \phi }$ , welche verschiedene Multiskalenanalysen erzeugen können, und dementsprechend zwei verschiedene Waveletfunktionen $\psi ,{\tilde \psi }$ . Die zwei Skalierungsfolgen müssen nun für alle ganzzahligen m folgende Biorthogonalitätsbedingung erfüllen:

$\sum _{{n\in \mathbb{Z } }}a_{n}{\tilde a}_{{n+2m}}=2\delta _{{m,0}}$

Ist diese erfüllt, ergeben sich die Waveletfolgen als

${\begin{alignedat}{2}b_{n}&=(-1)^{n}{\tilde a}_{{M-1-n}}&\qquad &{\mathrm {f{\ddot u}r}}\quad n=0,\ldots ,M-1\\{\tilde b}_{n}&=(-1)^{n}a_{{M-1-n}}&&{\mathrm {f{\ddot u}r}}\quad n=0,\ldots ,N-1\end{alignedat}}$

wobei N die Länge der Skalierungsfolge zu $\phi$ und M die Länge der Skalierungsfolge zu ${\tilde \phi }$ ist.

Der Jpeg-2000-Standard benutzt zur Bildkompression auch das biorthogonale Daubechies-5/3-Wavelet (auch als LeGall-5/3-Wavelet bekannt) für verlustfreie und das Daubechies-9/7-Wavelet (auch als Cohen-Daubechies-Feauveau 9/7 oder „CDF 9/7“ oder FBI-Fingerabdruck-Wavelet bekannt) für verlustbehaftete Kompression.

Analytische Bedingungen

Verschwindende Momente und Polynomapproximation

Eine notwendige Bedingung für die Existenz einer r-fach stetig differenzierbaren Lösung (r=0 für nur stetig) der Verfeinerungsgleichung ist, dass das Polynom (1+Z)^r+1 die erzeugende Funktion bzw. Z-Transformation $a(Z):=a_{0}+a_{1}Z+\dots +a_{{N-1}}Z^{{N-1}}$ der Skalierungsfolge a teilt. Die maximale Potenz A, so dass (1+Z)^A ein Faktor von a(Z) ist, heißt polynomiale Approximationsordnung. Sie gibt die Fähigkeit der Skalierungsfunktion an, Polynome bis zum Grad A-1 als Linearkombination ganzzahliger Verschiebungen der Skalierungsfunktion $\phi$ darzustellen.

Im biorthogonalen Fall ergibt eine Approximationsordnung A von $\phi$ eine gleiche Anzahl A von verschwindenden Momenten des dualen Wavelets ${\tilde \psi }$ , was daraus folgt, dass (1+Z)^A ein Faktor von $b(Z)=Z^{{-1}}a(-Z^{{-1}})$ ist. Umgekehrt ist die Approximationsordnung Ã von ${\tilde \phi }$ gleich zur Anzahl Ã von verschwindenden Momenten des Wavelets $\psi$ .
Im orthogonalen Fall stimmen A und Ã überein, wie auch $\phi ={\tilde \phi }$ und $\psi ={\tilde \psi }$ ist.

Glattheit der Funktionen

Ein Kriterium für die Lösbarkeit der Verfeinerungsgleichung ist das folgende: Faktorisieren wir $a(Z)=2^{{1-A}}(1+Z)^{A}p(Z)$ , ein Polynom in mit $p(1)=1$ , und gibt es eine Schranke der Art

$1\leq \sup _{{t\in [0,2\pi ]}}|p(e^{{it}})|<2^{{A-1-r}}$ für ein $r\in\N$ ,

so hat die Verfeinerungsgleichung eine -fach stetig differenzierbare Lösung mit Träger im Intervall $\left[0,N-1\right]$ , wobei $N=A+deg(p)+1$ .

Beispiele

$a(Z):=2^{{1-A}}(1+Z)^{A}$ , wozu ein konstantes $p(Z)=1$ gehört. Nach obigem muss $n<A-1$ gelten, d.h. die Lösungen wären mindestens $A-2$ -fach stetig differenzierbar. In der Tat sind die Lösungen aber gerade Schoenbergs B-Splines der Ordnung $A-1$ , die eine $(A-1)$ -te stückweise konstante Ableitung besitzen, insbesondere ist die $(A-2)$ -te Ableitung Lipschitz-stetig. Der Fall , der aus dieser Behandlung herausfällt, entspricht der Indexfunktion des Einheitsintervalls und ist die Skalierungsfunktion des Haar-Wavelets.
Im Fall und linear kann man ansetzen $a(Z)={\tfrac 14}(1+Z)^{2}\,((1+Z)+c(1-Z))$ . Bestimmen wir die Monomkoeffizienten dieses Polynoms 3. Grades und setzen diese 4 Koeffizienten in die Orthogonalitätsbedingung ein, so verbleibt am Ende genau die Bedingung $c_{2}=3$ . Setzen wir die positive Wurzel in ein, so erhalten wir die Skalierungsfolge des D4-Wavelets, siehe auch die Tabelle unten.

Konstruktion

Die Daubechies-Wavelets entsprechen dem Fall minimaler Freiheitsgrade in der Bestimmung der Skalierungsfolgen. Einerseits kann bei gegebener Anzahl von Verschwindungsmomenten die minimale Länge der Skalierungsfolge gesucht werden, andererseits die maximale Anzahl von Verschwindungsmomenten bei gegebener Länge. In beiden Fällen gilt $N=2A$ .

Orthogonale Wavelets

Verwenden wir die obige Faktorisierung der Skalierungsfolge, $a(Z)=2^{{1-A}}(1+Z)^{A}p(Z)$ , mit $p(1)=1$ , so können die Orthogonalitätsbedingungen ebenfalls in einem Laurent-Polynom zusammengefasst werden:

$a(Z)a(Z^{{-1}})+a(-Z)a(-Z^{{-1}})=4\quad \Rightarrow \quad (1-u)^{A}p(Z)p(Z^{{-1}})=1-u^{A}\,[p(-Z)p(-Z^{{-1}})]$

mit dem Kürzel $u:=1/4\cdot (2-Z-Z^{{-1}})$ . Aus dieser Gleichung leitet sich ab, dass $degp<A-1$ nicht funktionieren kann, somit mindestens $degp=A-1$ gilt, woraus $N=2a$ im minimalen Fall folgt.

Wir können mit der inversen Potenzreihe zu $(1-u)^{A}$ multiplizieren und an der Potenz $u^{A}$ abbrechen,

$p(Z)p(Z^{{-1}})=\sum _{{k=0}}^{{A-1}}{\binom {-A}{k}}(-u)^{k}=\sum _{{k=0}}^{{A-1}}{\binom {A+k-1}{k}}u^{k}$ .

Diese Gleichung ist lösbar, ihre Lösungen ergeben sich aus einer Methode, die spektrale Faktorisierung genannt wird. Zuerst werden die Nullstellen der rechten Seite als Polynom in bestimmt. Daraus ergeben sich $A-1$ quadratische Gleichungen mit zueinander reziproken Lösungen, eine davon wird $p(Z)$ zugeordnet. Daher ergeben sich $2^{A-1}$ mögliche Lösungen, man kann sich z.B. für diejenige entscheiden, bei der alle Nullstellen von $p(Z)$ innerhalb bzw. alle außerhalb des Einheitskreises liegen.

In der folgenden Tabelle sind die so erhaltenen Skalierungsfolgen für die Wavelets D2-D20, d.h. für A=1 bis $A=10$ , aufgelistet.

Orthogonale Daubechies-Koeffizienten
D2 (Haar)	D4	D6	D8	D10	D12	D14	D16	D18	D20
1	0,6830127	0,47046721	0,32580343	0,22641898	0,15774243	0,11009943	0,07695562	0,05385035	0,03771716
1	1,1830127	1,14111692	1,01094572	0,85394354	0,69950381	0,56079128	0,44246725	0,34483430	0,26612218
	0,3169873	0,650365	0,8922014	1,02432694	1,06226376	1,03114849	0,95548615	0,85534906	0,74557507
	−0,1830127	−0,19093442	−0,03967503	0,19576696	0,44583132	0,66437248	0,82781653	0,92954571	0,97362811
		−0,12083221	−0,26450717	−0,34265671	−0,31998660	−0,20351382	−0,02238574	0,18836955	0,39763774
		0,0498175	0,0436163	−0,04560113	−0,18351806	−0,31683501	−0,40165863	−0,41475176	−0,35333620
			0,0465036	0,10970265	0,13788809	0,1008467	6,68194092e−4	−0,13695355	−0,27710988
			−0,01498699	−0,00882680	0,03892321	0,11400345	0,18207636	0,21006834	0,18012745
				−0,01779187	−0,04466375	−0,05378245	−0,02456390	0,04345268	0,13160299
				4,71742793e−3	7,83251152e−4	−0,02343994	−0,06235021	−0,09564726	−0,10096657
					6,75606236e−3	0,01774979	0,01977216	3,54892813e−4	−0,04165925
					−1,52353381e−3	6,07514995e−4	0,01236884	0,03162417	0,04696981
						−2,54790472e−3	−6,88771926e−3	−6,67962023e−3	5,10043697e−3
						5,00226853e−4	−5,54004549e−4	−6,05496058e−3	−0,01517900
							9,55229711e−4	2,61296728e−3	1,97332536e−3
							−1,66137261e−4	3,25814671e−4	2,81768659e−3
								−3,56329759e−4	−9,69947840e−4
								−5,5645514e−5	−1,64709006e−4
									1,32354367e−4
									−1,875841e−5

Die Waveletkoeffizienten können abgeleitet werden, indem die Reihenfolge und das Vorzeichen für jeden zweiten Koeffizienten umgekehrt wird. Für D4 wäre dies z.B. −0,1830127, −0,3169873, 1,1830127, −0,6830127.

Biorthogonale symmetrische Wavelets

Eng verwandt zu den Daubechies-Wavelets sind die Cohen-Daubechies-Feauveau-Wavelets (CDF-Wavelets). Im Gegensatz zu den Daubechies-Wavelets sind letztere jedoch nur paarweise orthogonal (biorthogonal), dafür aber symmetrisch.

CDF-Wavelets erlangten Bekanntheit, da sie im JPEG-2000-Standard Verwendung finden. Weiterhin ist das Wavelet, das in der Fingerabdruckdatenbank des FBI eingesetzt wird, ein CDF-Wavelet.

Siehe auch

Haar-Wavelet

Basierend auf einem Artikel in:

Wikipedia.de