Anzahldichte

Die Anzahldichte ist eine Größe, die beschreibt, wie viele zählbare Dinge eines Typs pro Volumenelement vorkommen. Diese Dinge können Objekte, aber auch abstrakte Entitäten wie Ereignisse sein. Bei der Anzahldichte handelt es sich, wie bei allen Dichten, um eine intensive Größe.

Am häufigsten ist die Anzahldichte von Objekten in einem Raumvolumen von Interesse. Deshalb wird die Definition nachfolgend für diese Größe gegeben. Es ist nach diesem Vorbild einfach, sie analog für ebene oder gekrümmte Flächen oder eindimensionale Gebilde (Strecken, Polygonzüge, ebene Kurven, Raumkurven) zu bilden.

Überblick durch Beispiele

In Fachgebieten wie Physik, Astronomie, Chemie, Biologie, Ökologie sind oft Teilchen im engeren Sinne wie Atome, Moleküle, Elektronen, Nukleonen, Photonen oder Sterne, Galaxien etc. gemeint. Die Anzahldichte ist dann gegeben als Anzahl dieser Teilchen, die in einem Bereich des physikalischen Raumes enthalten sind, geteilt durch das Volumen oder den Flächeninhalt oder die Länge des betrachteten Bereichs. Diese Fälle können, wenn nötig, durch die Namen räumliche Anzahldichte (englisch Volume number density), flächenbezogene Anzahldichte (englisch Area number density) oder längenbezogene Anzahldichte (englisch Line number density) unterschieden werden.

Der betrachtete Raumbereich kann durch die Objekte selbst definiert sein, wie zum Beispiel die Grenzen eines Festkörpers, oder auch einfach ein beliebiger Teil des physikalischen Raums. Der Raumbereich kann offen sein, braucht also nicht unbedingt eine materielle Grenze, eine geschlossene materielle Oberfläche, zu besitzen.

In Fachgebieten wie Bevölkerungsgeographie, Demografie, Sozialwissenschaften werden Individuen oder Subjekte gezählt. Mit Bevölkerungsdichte wird die flächenbezogene Anzahldichte der Einwohner eines Staats, einer Stadt usw. bezeichnet. Die Individuen sind die Einwohner, ihre flächenbezogene Dichte ist die Bevölkerungsdichte.

Atomanzahldichten der chemischen Elemente

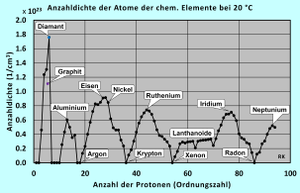
Anzahldichten der Atome der chemischen Elemente bei 20 °C und 1000 hPa. Die Anzahldichten der Atome der 11 bei dieser Temperatur und Druck gasförmigen Elemente liegen in der Größenordnung von 10¹⁹ Atomen pro Kubikzentimeter und erscheinen deshalb in der Abbildung, als wären sie Null.

Die Abbildung zeigt die Anzahldichten der Atome (Atomanzahldichten) der chemischen Elemente bei 20 °C als ein Beispiel für die physikalische Größe Anzahldichte. Hervorzuheben ist die Tatsache, dass Kohlenstoff in der Natur in reiner Form als Diamant und als Graphit vorkommt. Diese Kohlenstoffmodifikationen besitzen deutlich unterschiedliche Massendichten und somit auch Atomanzahldichten. Ihre Atomanzahldichten sind in der Abbildung als blauer zw. violetter Punkt hervorgehoben. Kohlenstoff in der Modifikation Diamant hat die mit Abstand größte Atomanzahldichte aller Elemente.

Atomanzahldichte eines idealen Gases

Bei einem Gas bestimmt außer der Temperatur der Druck des Gases die Atomanzahldichte, wobei hier als Beispiel eine Standardbedingung gemäß Maßbezugstemperatur für physikalische Größen gewählt werden soll. Die Temperatur sei 20 °C, die absolute Temperatur folglich $T=293{,}15\ \mathrm {K}$ , der Druck $p=1,01325\cdot 10^{5}\ \mathrm {Pa}$ . Für ein ideales Gas ergibt sich die Atomanzahldichte zu

$n={\frac {p}{k_{\mathrm {B} }\cdot T}}$ .

Dabei ist $k_{\mathrm {B} }=1{,}38065\cdot 10^{-23}\ \mathrm {J/K}$ , die Boltzmann-Konstante. Werden die Zahlenwerte in diese Formel eingesetzt, ergibt sich die Atomanzahldichte des idealen Gases zu

$n=2{,}5035\cdot 10^{19}{\frac {\text{Atome}}{\mathrm {cm^{3}} }}$

(siehe auch Satz von Avogadro). Die oben angegebenen Atomanzahldichten der 6 natürlich vorkommenden Edelgase weichen nur geringfügig von der Atomanzahldichte des idealen Gases ab. Die größe Abweichung ist bei Helium mit $n=2{,}5577\cdot 10^{19}{\text{Atomen}}/\mathrm {cm^{3}}$ zu vermerken.

Definition

Die räumliche Anzahldichte ist gleich der Anzahl $\mathrm {d} N$ der Objekte, die in einem Raumbereich $\mathrm {d} V$ enthalten sind, geteilt durch das Volumen des Raumbereichs

$n({\vec {x}})={\frac {\mathrm {d} N}{\mathrm {d} V}}$

Da diese mathematisch strikte Definition der Anzahldichte im Allgemeinen unpraktikabel ist – für als punktförmig angenommene Atome in einem Kristall würde sich die Anzahldichte beispielsweise als Dirac-Kamm manifestieren –, wird die Anzahldichte in Gebieten, in denen makroskopische Größen untersucht werden, nicht über ein infinitesimales Volumenelement, sondern über einen mesoskopischen Raumbereich $\Delta V$ definiert. Dieser mesoskopische Raumbereich muss so gewählt sein, dass eine Mittelung der Größen in diesem Bereich keinen Einfluss auf die makroskopische Physik hat.

Der arithmetische Mittelwert $\overline{n}$ einer räumlich variierenden Anzahldichte im Raumbereich mit dem Volumen wird durch

${\overline {n}}={\frac {\iiint _{V}n({\vec {x}})\,\mathrm {d} V}{\iiint _{V}\mathrm {d} V}}={\frac {N}{V}}$

bestimmt. Die Anzahl aller Objekte in einem Raumbereich mit dem Volumen wird durch Integration berechnet,

$N=\iiint _{V}n({\vec {x}})\,\mathrm {d} V,$ ,

wobei $\mathrm {d} V$ das Volumenelement des Raumbereichs ist. Besitzen alle Objekte die gleiche Masse $m_{0}$ , ist die totale Masse aller Objekte im Raumbereich mit dem Volumen

$M=m_{0}\iiint _{V}n({\vec {x}})\,\mathrm {d} V.$ .

Ähnliche Formeln gelten für andere extensive Größen, die aus Anzahldichten zählbarer Objekte gebildet werden. Für die elektrische Ladung beispielsweise wird die Masse durch die Gesamtladung und die Masse $m_{0}$ eines Objekts durch die Ladung $q_{0}$ eines Objekts in der letzten Formel ersetzt.

Einheit

Die SI-Einheit der räumlichen Anzahldichte ist m⁻³, oft wird jedoch die Einheit cm⁻³ verwendet.

Der im Zähler stehenden physikalischen Größe Anzahl ist als Größe der Dimension Zahl im SI-Einheitensystem keine Maßeinheit zugeordnet, die Beifügung eines Hilfsworts, beispielsweise „Stück“, „Einheit[en]“, „Paar“, „Satz“ oder die Bezeichnung der gezählten Objekte/Subjekte (wie zum Beispiel 12 Bäume oder 24 Teilchen) wird jedoch toleriert.

Beispiele für Namensvarianten

Es gibt einige Namensvarianten, mit denen eine Größe Anzahldichte gemeint ist. Stellvertretend sollen hier zwei Beispiele genannt werden.

Objektdichte

→ Hauptartikel: Teilchendichte

In der Literatur finden sich folgende drei Namensvarianten: Anzahldichte der Objekte, Objektanzahldichte, Objektdichte. Sind die Objekte Teilchen, so führt das auf die Namensvarianten Anzahldichte der Teilchen, Teilchenanzahldichte, Teilchendichte, zum Beispiel Anzahldichte der Atome, Atomanzahldichte, Atomdichte. Nur in den jeweils ersten Namensvarianten kommt durch den Plural schon im Namen zum Ausdruck, dass es sich um eine Größe für viele Objekte, Teilchen oder Atome handelt. Die jeweils dritten Namensvarianten sind doppeldeutig. Es könnte auch die Massendichte eines Objekts, Teilchens oder Atoms gemeint sein. Gibt es für das Objekt Synonyme, vermehren sich die Namensvarianten weiter, zum Beispiel wenn man statt von Teilchen von Partikeln spricht.

Beispiele, wie Anzahldichten ermittelt werden

Es gibt unterschiedliche Methoden, die Anzahldichte zu bestimmen. Sind Anzahldichten mehrerer Typen von Objekten/Subjekten zu bestimmen, kann das in den allermeisten Fällen auf einen Typ eingeschränkt werden. Nachfolgend wird angenommen, dass nur ein Typ im Raumbereich enthalten ist.

Anzahldichte durch Zählen bestimmen

Unabhängig davon, welche Art einer Anzahldichte berechnet werden soll, am Anfang steht das Zählen. Bereits beim Zählen mit dem Zeigefinger setzt der Mensch sein Abstraktionsvermögen ein.

Eine Anzahldichte der Ökologie ist die Populationsdichte oder Bestandsdichte. Sie betrachtet die Größe einer Population in einem Raumbereich oder einem Flächengebiet. Beispiele für die zu zählenden Objekte sind Fische oder Planktonorganismen in einem See, Bakterien in einem Tank oder Bodenorganismen. Flächenbezogene Populationsdichte werden in Einheiten Individuen pro Quadratmeter, pro Hektar usw. angegeben. Populationsdichten von Vögeln werden insbesondere im Umfeld von Flughäfen bestimmt. Bei der Populationsdichte einer Art speziell in ihrem Siedlungsgebiet wird die Anzahldichte Abundanz genannt.

Anzahldichte durch Massenvergleich bestimmen

Jedes der Objekte im Raumbereich besitze die Masse $m_{0}$ und die Gesamtmasse aller Objekte sei . Um die Objekte im Raumbereich zu zählen, kann in der klassischen Mechanik die Masse aller Objekte und die Masse eines einzelnen Objekts gemessen und daraus die Anzahl der Objekte berechnet werden:

$N={\frac {M}{m_{0}}}$

Ist das Volumen des Raumbereichs bestimmt, folgt daraus die Anzahldichte

$n={\frac {M}{V\cdot m_{0}}}$ .

Eine verbreitete Anwendung dieser Formel ist die Berechnung der Anzahldichte für Atome bei gegebener Massendichte und der Masse eines Atoms in einem gegebenen Raumbereich.

Basierend auf einem Artikel in:

Wikipedia.de