Linearisierung

Bei der Linearisierung werden nichtlineare Funktionen oder nichtlineare Differentialgleichungen durch lineare Funktionen oder durch lineare Differentialgleichungen angenähert. Die Linearisierung wird angewandt, da lineare Funktionen oder lineare Differentialgleichungen einfach berechnet werden können und die Theorie umfangreicher als für nichtlineare Systeme ausgebaut ist.

Tangente

Tangenten an $f(x)=\sin(x)$ :
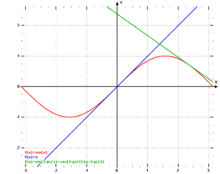
blau

grün $x_{0}={\tfrac {3\cdot \pi }{4}}$

Das einfachste Verfahren zur Linearisierung ist das Einzeichnen der Tangente in den Graphen. Daraufhin können die Parameter der Tangente abgelesen werden, und die resultierende lineare Funktion (Punktsteigungsform der Geraden)

$y_{t}=f(x_{0})+{\frac {\mathrm {d} f}{\mathrm {d} x}}{\bigg |}_{x_{0}}\cdot (x-x_{0})$

approximiert die Originalfunktion um den Punkt $x_{0}$ . Dabei ist ${\tfrac {\mathrm {d} f}{\mathrm {d} x}}{\bigg |}_{x_{0}}$ der Anstieg im Punkt $x_{0}$ .

Wenn die Funktion in analytischer Form vorliegt, kann die Gleichung der Tangente direkt angegeben werden.

Der relative Fehler der Approximation ist

$F(x)=\bigg| \frac{f(x)-y_t(x)}{f(x)} \bigg|$

Für die Funktion $f(x)=\sin(x)$ gilt beispielsweise:

$y(x)=\sin (x_0) + \cos (x_0) \cdot (x-x_0)$

Die Bestimmung der Tangente entspricht der Bestimmung des linearen Glieds des Taylorpolynoms der zu approximierenden Funktion.

Anwendungen

Anwendung findet die Linearisierung unter anderem in der Elektrotechnik und der Regelungstechnik zur näherungsweisen Beschreibung nichtlinearer Systeme durch lineare Systeme.

Das Ergebnis einer Netzwerkanalyse ist unter Umständen ein nichtlineares Gleichungssystem. Dies kann unter gewissen Voraussetzungen in ein lineares Gleichungssystem überführt werden. Nicht die einzige, aber die einfachste Methode der Linearisierung ist die Linearisierung in einem Arbeitspunkt (kurz „AP“). Nur diese ist in den folgenden Abschnitten beschrieben.

Linearisierung der Multiplikation

In einem Signalflussplan lassen sich komplexe Systeme durch ein Blockbild darstellen, das zur qualitativen Visualisierung von mathematischen Modellen dient.

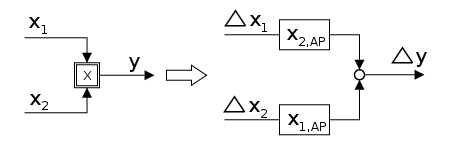
Eine Multiplikation im Signalflussplan ersetzt durch eine Addition $\Delta y=\Delta x_{1}\cdot x_{2,{\text{AP}}}+\Delta x_{2}\cdot x_{1,{\text{AP}}}$
(Arbeitspunkte $x_{1,{\text{AP}}}$ , $x_{2,{\text{AP}}}$ und $y_{\text{AP}}$ wurden zur übersichtlicheren Darstellung weggelassen)

Befindet sich in diesem Signalflussplan eine Multiplikationsstelle, so lässt sich diese durch Linearisierung in eine Additionsstelle umwandeln.

Im Folgenden bezeichnen wir mit das Produkt zweier Zahlen $x_{1}$ und $x_{2}$ :

$y = x_1 \cdot x_2$

Im Arbeitspunkt können wir die Multiplikation linearisieren, indem wir $x_{1}$ als Summe des Arbeitspunkts und der Differenz $\Delta x_{1}=x_{1}-x_{1,{\text{AP}}}$ schreiben:

$y=(x_{1,{\text{AP}}}+\Delta x_{1})\cdot (x_{2,{\text{AP}}}+\Delta x_{2})$

Wir können dieses Produkt nach dem Distributivgesetz ausmultiplizieren. Es ergibt sich die Summe:

$y=x_{1,{\text{AP}}}\cdot x_{2,{\text{AP}}}+x_{1,{\text{AP}}}\cdot \Delta x_{2}+x_{2,{\text{AP}}}\cdot \Delta x_{1}+\Delta x_{1}\cdot \Delta x_{2}$

Wir nehmen nun an, dass das Verhältnis der Abweichungen vom Arbeitspunkt $\Delta x_{i}$ und dem Arbeitspunkt selber klein ist:

${\frac {\Delta x_{i}}{x_{i,{\text{AP}}}}}\ll x_{i,{\text{AP}}}$ und somit auch das Produkt $e_{y}=\Delta x_{1}\cdot \Delta x_{2}$ klein ist. Die linearisierte Multiplikation lautet also:

$y\approx x_{1,{\text{AP}}}\cdot x_{2,{\text{AP}}}+x_{1,{\text{AP}}}\cdot \Delta x_{2}+x_{2,{\text{AP}}}\cdot \Delta x_{1}$

Beispiel

Wähle die Zahlen:

$x_{1}=2{,}4;\ x_{2}=110\Rightarrow y=x_{1}\cdot x_{2}=264.$

Nun stellt sich, die Frage, wie die Arbeitspunkte zu wählen sind. Um die Rechnung zu vereinfachen, runden wir $2{,}4$ auf ab und 110 auf 100 ab: Wähle also: $x_{1,{\text{AP}}}=2;\ x_{2,{\text{AP}}}=100\Rightarrow \Delta x_{1}=0{,}4;\ \Delta x_{2}=10.$ Das linearisierte Produkt ist also

$\Rightarrow y \approx 2 \cdot 100 + 2 \cdot 10 + 100 \cdot 0{,}4 = 260$

mit dem Fehler $e_y = 0{,}4 \cdot 10 = 4$ .

Linearisierung der Division

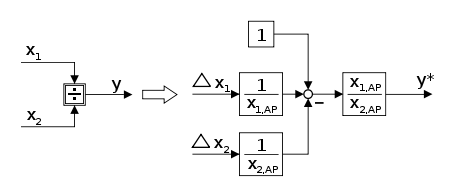
Linearisierung einer Division dargestellt im Signalflussplan

Wir betrachten nun den Quotienten zweier Zahlen $x_{1}$ und $x_{2}$ :

$y=\frac{x_1}{x_2}$

Analog wie zur Multiplikation entwickeln wir $x_{i}=x_{i,{\text{AP}}}+\Delta x_{i}$ um den Arbeitspunkt $x_{\text{AP}}$ . Damit können wir den Quotienten wie folgt schreiben:

$y={\frac {x_{1,{\text{AP}}}+\Delta x_{1}}{x_{2,{\text{AP}}}+\Delta x_{2}}}$

Ausklammern der Arbeitspunkte liefert für Division:

$y={\frac {x_{1,{\text{AP}}}}{x_{2,{\text{AP}}}}}\cdot {\frac {1+{\frac {\Delta x_{1}}{x_{1,{\text{AP}}}}}}{1+{\frac {\Delta x_{2}}{x_{2,{\text{AP}}}}}}}$

Wir wollen nun den Zähler und den Nenner des Bruches linearisieren. Dazu verwenden wir die geometrische Reihe. Für eine Nullfolge $q^{k}$ gilt:

$\sum_{k=0}^{n}q^k=\frac{1-q^{n+1}}{1-q}$

Hierbei ist entsprechend $q=-{\tfrac {\Delta x_{2}}{x_{2,{\text{AP}}}}}$ mit $\vert q \vert \ll 1$ zu wählen.

Einsetzen liefert die Linearisierung

${\frac {1}{1+{\frac {\Delta x_{2}}{x_{2,{\text{AP}}}}}}}\approx 1-{\frac {\Delta x_{2}}{x_{2,{\text{AP}}}}}$

Analog lässt sich der Nenner des obigen Bruchs linearisieren. Die linearisierte Division lässt sich schreiben durch:

$y\approx {\frac {x_{1,{\text{AP}}}}{x_{2,{\text{AP}}}}}\cdot \left(1+{\frac {\Delta x_{1}}{x_{1,{\text{AP}}}}}-{\frac {\Delta x_{2}}{x_{2,{\text{AP}}}}}\right)$

Linearisieren gewöhnlicher Differentialgleichungen

Ein bekanntes Beispiel für die Linearisierung einer nichtlinearen Differentialgleichung ist das Pendel. Die Gleichung lautet:

$\ddot y(t)+D\cdot \dot y(t)+\omega ^2\sin(y(t))=0$

Der nichtlineare Teil ist $\sin(y)$ . Dieser wird für kleine Schwankungen um einen Arbeitspunkt $y_{0}$ approximiert durch:

$\sin (y) \approx \sin (y_0) + \cos (y_0) \cdot (y-y_0)$

Mit dem Arbeitspunkt $y_{0}=0$ gilt:

$\sin(y)\approx y$ und damit die linearisierte Differenzialgleichung

$\ddot y(t)+D\cdot \dot y(t)+\omega ^2\cdot y(t)=0$ .

Diese linearisierten Differentialgleichungen sind meist deutlich einfacher zu lösen. Für ein mathematisches Pendel (wähle $D=0$ ) lässt die Gleichung durch einfache Exponentialfunktionen lösen, wobei die nicht-linearisierte nicht analytisch lösbar ist. Weitere Details über das Linearisieren von Differentialgleichungen sind in dem Artikel über die Zustandsraumdarstellung beschrieben.

Tangentialebene

Darstellung als Signalflussplan

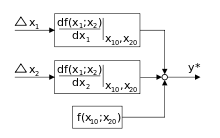
Soll eine gegebene Funktion $f(x_{1},x_{2})$ in einem Punkt $x_{10},x_{20}$ linearisiert werden, wird sich der Taylor-Formel bedient. Das Ergebnis entspricht der Tangentialebene in diesem Punkt.

Für die Funktion $f(x_{1},x_{2})$ gilt in der Umgebung des Punktes $x_{10},x_{20}$ :

$y=\underbrace {f(x_{10},x_{20})} _{={\text{const.}}}+\underbrace {{\frac {\partial f(x_{1},x_{2})}{\partial x_{1}}}{\bigg |}_{x_{10},x_{20}}\cdot (x_{1}-x_{10})+{\frac {\partial f(x_{1},x_{2})}{\partial x_{2}}}{\bigg |}_{x_{10},x_{20}}\cdot (x_{2}-x_{20})} _{=\Delta y}$

Beispiel:

$f(x_{1},x_{2})=x_{1}\cdot x_{2}$

ergibt die Tangentialebene

$y=\underbrace {x_{10}\cdot x_{20}} _{={\text{const.}}}+\underbrace {x_{20}\cdot (x_{1}-x_{10})+x_{10}\cdot (x_{2}-x_{20})} _{=\Delta y}$

Siehe auch

Taylor-Reihe

Basierend auf einem Artikel in:

Wikipedia.de