
Scheitelpunkt
Scheitelpunkte, kurz Scheitel, sind in der Geometrie besondere Punkte auf Kurven.
Die Scheitelpunkte eines Kegelschnitts (Ellipse, Parabel oder Hyperbel) sind die Schnittpunkte der Kurve mit den Symmetrieachsen. Sie sind gleichzeitig die Punkte, an denen die Krümmung maximal oder minimal ist.
Der Scheitelpunkt einer aufrecht stehenden Parabel, die Funktionsgraph einer quadratischen Funktion ist, ist Hochpunkt oder Tiefpunkt des Graphen. Durch die Lage des Scheitelpunkts und den Streckfaktor ist der Graph einer quadratischen Funktion eindeutig bestimmt. Die rechnerische Bestimmung des Scheitelpunkts ist somit ein wichtiges Hilfsmittel, um den Graph einer quadratischen Funktion zu zeichnen.
Allgemeiner bezeichnet man in der Differentialgeometrie einen Punkt auf einer regulären Kurve als Scheitel oder Scheitelpunkt, wenn die Krümmung dort ein lokales Extremum (also ein lokales Maximum oder Minimum) besitzt. Der Vierscheitelsatz macht eine Aussage über die Existenz und die Anzahl von Scheitelpunkten bei einfach geschlossenen glatten ebenen Kurven.
Scheitelpunkt eines Kegelschnitts
Die Scheitelpunkte eines Kegelschnitts sind die Schnittpunkte einer solchen Kurve mit deren Symmetrieachsen. Die Ellipse hat vier Scheitel, zwei Hauptscheitel und zwei Nebenscheitel, bei der Hyperbel treten zwei auf, bei der Parabel nur einer, der Kreis hat keinen expliziten Scheitelpunkt.
Scheitelpunkt einer Parabel
Der Graph einer quadratischen Funktion ist eine Parabel. Ihr Scheitelpunkt ist identisch mit dem Hochpunkt (lokales Maximum), wenn sie nach unten geöffnet ist, und identisch mit dem Tiefpunkt (lokales Minimum), wenn sie nach oben geöffnet ist.
Wenn die Lage des Scheitelpunktes bekannt ist, kann die Parabel, soweit es sich um eine Normalparabel handelt, mit Hilfe einer Parabelschablone schnell in ein Koordinatensystem gezeichnet werden. Man kann die Parabelschablone auch zum Zeichnen von Parabeln verwenden, die keine Normalparabeln sind, wenn man das Koordinatensystem entsprechend skaliert.
Scheitelpunktform
Unter der Scheitelform oder Scheitelpunktform einer quadratischen Funktion
versteht man eine bestimmte Form dieser Gleichung, aus welcher man den Scheitelpunkt der Funktion direkt ablesen kann.
Sie lautet
mit dem Scheitelpunkt .
Folglich kann die Funktion
in die Form
überführt werden.
Der Scheitelpunkt lautet dann
In der Schule wird diese Formel aufgrund ihrer Größe meistens nicht gelehrt. Stattdessen wird die quadratische Ergänzung gelehrt, mit deren Hilfe man eine quadratische Funktion von der Polynomform in die Scheitelpunktform überführt.
Herleitung mittels Verschiebung
Die Normalparabel
hat ihren Scheitel im Koordinatenursprung. Eine Streckung in y-Richtung mit dem
Streckungsfaktor
(Parabelgleichung
)
ändert daran nichts. Wird diese Parabel jetzt in x-Richtung um
Einheiten und in y-Richtung um
Einheiten verschoben, so dass ihr Scheitel die Koordinaten
besitzt, kann das mittels folgender Transformation dargestellt werden:
.
Durch Ausmultiplizieren erhält man:
und daraus
.
Vergleich mit der Standardfunktionsgleichung
liefert:
und
.
Dies kann umgeformt werden zu
bzw.
.
Herleitung mittels quadratischer Ergänzung
Die obige Formel kann mithilfe der quadratischen Ergänzung hergeleitet werden. Die allgemeine Form wird in die Scheitelpunktform umgeformt.
Daraus können die Koordinaten des Scheitelpunktes direkt abgelesen werden:
.
Herleitung mittels Ableitung
Da die Steigung im Scheitelpunkt gleich 0 ist, ist es möglich mit Hilfe der ersten Ableitung die obige Formel herzuleiten.
Einsetzen in die Normalform:
Beispiele
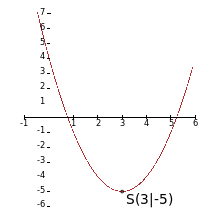
Beispiel 1
hat den Scheitelpunkt
, also
Beispiel 2
Mit ,
und
berechnet sich der Scheitelpunkt zu
, also
Bestimmung der Nullstellen aus der Scheitelpunktform
Aus der Scheitelpunktform lassen sich sehr einfach die Nullstellen der jeweiligen quadratischen Funktion bestimmen.
Substituiert man
mit
und
mit
,
ergibt sich die Form
mit dem Scheitelpunkt
.
Bestimmung der Nullstellen:
Ersetzt man
und
wieder durch
und
,
ergibt sich die a-b-c-Formel:


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 20.10. 2020