Catalansche Fläche

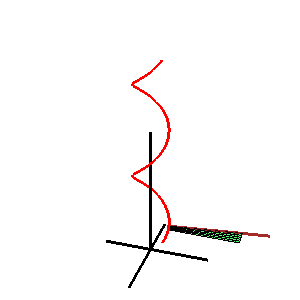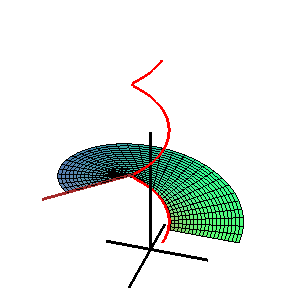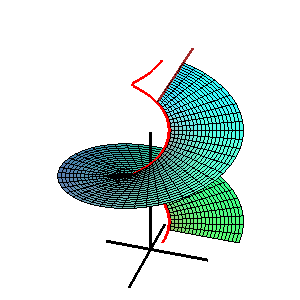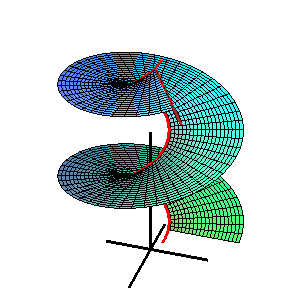
Catalansche Fläche: Beispiel Wendelfläche
Leitkurve ist eine Helix, Richtebene ist die x-y-Ebene

Eine Catalansche Fläche ist in der Geometrie eine nach dem belgischen Mathematiker Eugène Charles Catalan benannte Regelfläche, deren Erzeugenden (Geraden) alle zu einer festen Ebene, der Richtebene, parallel sind.

Eine Catalansche Fläche mit der Richtebene ${\mathbf x}\cdot {\mathbf n}_{0}=0$ lässt sich durch eine Parameterdarstellung

${\mathbf x}(u,v)={\mathbf c}(u)+v{\mathbf r}(u)\ ,$ mit

${\mathbf r}(u)\cdot {\mathbf n}_{0}=0$

beschreiben. Jede Flächenkurve ${\mathbf x}(u_{0},v)$ mit festem Parameter $u=u_{0}$ ist eine Erzeugende, ${\mathbf c}(u)$ beschreibt die Leitkurve und die Vektoren ${\mathbf r}(u)$ sind alle parallel zur Richtebene.

Ist ${\mathbf r}(u)$ hinreichend differenzierbar, kann man die Planaritätsbedingung auch durch

$\det({\mathbf r},{\mathbf {\dot r}},{\mathbf {\ddot r}})=0$

ausdrücken.

Beispiele:

(1) Ebene: ${\mathbf x}(u,v)={\mathbf p}+u{\mathbf a}+v{\mathbf r}$

Die Leitkurve ist eine Gerade.

(2) Zylinder: ${\mathbf x}(u,v)=(\cos u,\sin u,0)+v(0,0,1)$

Die Leitkurve ist ein Kreis. Als Richtebene kann man jede Ebene parallel zur z-Achse verwenden.

(3) Wendelfläche: ${\mathbf x}(u,v)=(\cos u,\sin u,u)+v(\cos u,\sin u,0)$

Die Leitkurve ist eine Helix (Schraublinie) und die Richtebene parallel zur x-y-Ebene.

Diese Wendelfläche lässt sich auch mit einer Gerade (z-Achse) als Leitkurve erzeugen:

${\mathbf x}(u,v)=(0,0,u)+v(\cos u,\sin u,0)$

(4) Ein Konoid ist eine Catalansche Fläche, bei der sich die Geraden auf einer festen Gerade, der Achse, schneiden.

Catalan bewies, dass die Ebene und die Wendelfläche die einzigen Regelflächen unter den Minimalflächen sind.

Bemerkung:

Regelflächen, aber keine Catalansche Flächen sind z.B.: Kegel, einschaliges Hyperboloid.
Man sollte eine Catalansche Fläche nicht mit einer Catalanschen Minimalfläche verwechseln !

Siehe auch

Basierend auf einem Artikel in:

Wikipedia.de