Arbeit (Physik)

Name

Arbeit

Formelzeichen

Größen- und Einheitensystem	Einheit	Dimension
SI	J = kg·m²·s⁻² = N·m = W·s	L²·M·T⁻²
cgs	erg	L²·M·T⁻²

Arbeit (Formelzeichen von englisch work) ist in der Physik die Energie, die durch Kräfte auf einen Körper übertragen wird. Man sagt: „An dem Körper wird Arbeit verrichtet“. Das geschieht, indem eine Kraft längs eines Weges auf ihn einwirkt. Die geleistete Arbeit berechnet sich in diesem einfachsten Fall als Produkt aus der in Wegrichtung wirkenden Kraft mit der Wegstrecke. Bei nicht geradlinigen Wegen und nicht konstanten Kräften ist die Arbeit das Kurvenintegral über das Skalarprodukt aus Kraft und Weg.

Die SI-Einheit für Arbeit ist identisch mit der für Energie: das Joule (Einheitenzeichen J). Aus dem Bezug der Arbeit zur Kraft (SI-Einheit Newton) und Leistung (SI-Einheit Watt) ergeben sich die SI-abgeleiteten Einheiten Newtonmeter (Nm)^[1] und Wattsekunde (Ws): Es gilt 1 J = 1 Nm = 1 Ws. Häufig werden zudem die Einheiten Wattstunde (Wh) beziehungsweise Kilowattstunde (kWh) verwendet.

In der Thermodynamik ist die Arbeit eine Prozessgröße. Auf ein System kann Energie auf zwei Arten übertragen werden: In Form von Wärmezufuhr (z.B. durch Heizung) oder auf mechanische Weise (z.B. durch Kompression). Da bei der Kompression eine Kraft längs eines Weges wirkt, wird die übertragene Energie als Arbeit (Symbol ) bezeichnet. In beiden Fällen ändert sich gemäß dem ersten Hauptsatz der Thermodynamik die innere Energie des Systems.

Mit spezifischer Arbeit (Formelzeichen ) ist in der Thermodynamik das auf die Masse des Strömungsfluides bezogene Arbeitsvermögen, Einheit J/kg, gemeint (siehe auch Totalenthalpie).

Einführung

Schiebt man eine Tasse mit dem Finger unter gleichmäßigem Druck über den Tisch, beträgt die vom Finger auf die Tasse ausgeübte Kraft beispielsweise $F_{F}\,=\,1\ \mathrm {N}$ . Wird die Tasse um die Strecke $s\,=\,0{,}3\ \mathrm {m}$ verschoben, dann hat der Finger nach der Verschiebung die Arbeit

$W_{F}\,=\,F_{F}\cdot s\,=\,1\ \mathrm {N} \cdot 0{,}3\ \mathrm {m} \,=\,0{,}3\ \mathrm {Nm} \,=\,0{,}3\ \mathrm {Joule}$

an der Tasse geleistet.

Gemäß dem Dritten Newtonschen Gesetz übt während der Verschiebung die Tasse auf den Finger eine gleich große aber entgegengesetzt gerichtete Kraft $F_{T}\,=\,-F_{F}$ aus. Die Tasse leistet am Finger also die Arbeit

$W_{T}\,=\,F_{T}\cdot s\,=\,-F_{F}\cdot s\,=\,-W_{F}$ .

Das negative Vorzeichen bedeutet, dass die Arbeit dem Finger entzogen wird.

In Übereinstimmung mit dem Prinzip der Energieerhaltung ist die der Tasse in Form von Arbeit zugeführte Energie also gleich der dem Finger entzogenen Energie. Die Betrachtungsweisen „Finger leistet Arbeit an Tasse“ und „Tasse leistet Arbeit am Finger“ sind also gleichermaßen möglich, und es kann die in der vorliegenden Situation anschaulichere oder bequemere gewählt werden. Es ist jedoch stets auf das korrekte Vorzeichen zu achten und deutlich zu machen, welcher der beteiligten Körper als der die Arbeit leistende betrachtet wird.

Die Tasse leistet ihrerseits bei der Bewegung über die Tischplatte Reibungsarbeit. Die der Tasse zugeführte Arbeit wird letztlich vollständig in Wärme umgewandelt. Da die Bestimmungsgrößen der Arbeit – die aufgewandte Kraft und die zurückgelegte Strecke – leicht messbar sind, konnte J.P. Joule die bei seinen Versuchen zum mechanischen Wärmeäquivalent als Folge der aufgewandten mechanischen Arbeit freigesetzte Wärmemenge leicht anhand dieser Größen bestimmen. Auch andere Energieformen können auf ähnliche Weise auf die mechanische Arbeit zurückgeführt werden.

Fällt eine Kugel der Masse $m\,=\,1\ \mathrm {kg}$ durch eine zähe Flüssigkeit (z.B. Honig), liegen im Prinzip dieselben Verhältnisse vor. Aufgrund der Schwerebeschleunigung greift an der Kugel die konstante Gewichtskraft $F_{g}\,=\,m\cdot g\,=\,9{,}81\ \mathrm {N}$ an und leistet an der Kugel in jedem durchfallenen Meter die Arbeit $W_{g}\,=\,9{,}81\ \mathrm {J}$ . Diese Arbeit wird von der inneren Reibung der Flüssigkeit in Wärme umgewandelt.

Fällt die Kugel im Vakuum, tritt keine Reibung auf. Die von der Gewichtskraft an der Kugel geleistete Arbeit vermehrt daher kontinuierlich die kinetische Energie der Kugel, die sich also beschleunigt bewegt. Mit jedem durchfallenen Meter nimmt die kinetische Energie der Kugel um die an ihr geleistete Beschleunigungsarbeit $9{,}81\ \mathrm {J}$ zu.

Wie der Vergleich der letzten beiden Beispiele zeigt, kommt es nur auf die zurückgelegte Strecke (hier $1\ \mathrm {m}$ ) an, nicht jedoch auf die Geschwindigkeit, mit der die Strecke durchlaufen wird. Es ist unerheblich, ob die Kugel am Beginn der Messstrecke fallengelassen wird, oder ob sie aus großer Höhe kommend die Strecke mit großer Geschwindigkeit durchfällt.

Ist die Richtung der Kraft nicht parallel zur Richtung der Verschiebestrecke, dann kommt nur die zur Strecke parallele Kraftkomponente zur Wirkung. Steht die Kraft senkrecht zur Bewegungsrichtung, leistet sie keine Arbeit (ein Beispiel wäre ein seitlich auf einen fahrenden Zug wirkender Winddruck). Liegt die Kraft antiparallel zur Verschiebestrecke, ist die geleistete Arbeit negativ, wie im ersten Beispiel.

Definition

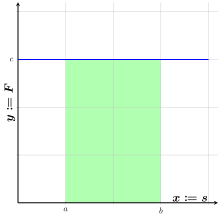
Kraft-Weg-Diagramm bei konstanter Kraft. Die markierte Fläche bemisst die verrichtete Arbeit.

Arbeit wird in der Mechanik definiert als das Skalarprodukt aus Kraft und Weg: Wenn auf einen Körper auf der geraden Strecke vom Punkt A zum Punkt B eine konstante Kraft ${\vec {F}}$ wirkt, dann wird am Körper die Arbeit

$W={\vec {F}}\cdot {\vec {s}}=|{\vec {F}}|\,|{\vec {s}}|\,\cos \sphericalangle \left({\vec {F}},{\vec {s}}\right)\,$

verrichtet. Dabei ist ${\vec s}$ der Verbindungsvektor von A nach B, und sein Skalarprodukt mit dem Vektor ${\vec {F}}$ ist das Produkt der Beträge $|{\vec F}|$ und $|{\vec s}|$ mal dem Kosinus des eingeschlossenen Winkels.

Die Bedeutung des physikalischen Begriffs Arbeit beruht auf folgendem Sachverhalt: Beschleunigt die betrachtete Kraft den Körper, so erhöht sich seine kinetische Energie auf dem Weg von A nach B um die an ihm verrichtete Arbeit.

Wirkt die konstante Kraft in Richtung des zurückgelegten Weges, dann ist die Arbeit das Produkt der Beträge $W=|{\vec F}|\,|{\vec s}|\,$ , da der Winkel null und sein Kosinus = 1 ist.

Ist die Richtung der Kraft der Bewegungsrichtung entgegengesetzt, dann bilden die beiden Vektoren einen Winkel von 180°, dessen Kosinus der Wert −1 ist. In diesem Fall wird an dem Körper eine negative Arbeit verrichtet, das heißt ihm wird Energie entnommen, er wird langsamer.

Ist die Richtung der Kraft senkrecht zum Weg, dann wird keine physikalische Arbeit verrichtet. Der physikalische Begriff entspricht also nicht dem alltäglichen Verständnis, nach dem jeder Kofferträger für seine verrichtete Arbeit bezahlt wird.

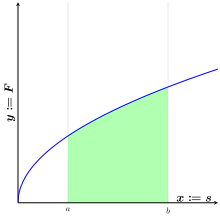
Kraft-Weg-Diagramm bei veränderbarer Kraft. Die markierte Fläche bemisst die verrichtete Arbeit.

Wenn die Kraft nicht entlang des gesamten Weges konstant ist oder der Weg nicht gerade ist, so kann man die Arbeit näherungsweise berechnen, indem man den Weg durch einen Streckenzug aus N geraden Teilstücken $\Delta {\vec s}_{i}$ mit $i=(1,2,3,\dots ,N)$ nähert, auf denen die Kraft ${\vec F}(s_{i})$ jeweils näherungsweise als konstant angenommen werden kann. Die entlang des gesamten Weges verrichtete Arbeit ergibt sich dann näherungsweise durch Summierung der Arbeiten entlang der einzelnen Wegstücke als

$W\approx \sum _{{i=1}}^{{N}}W_{i}=\sum _{{i=1}}^{{N}}{\vec F}({\vec s}_{i})\cdot \Delta {\vec s}_{i}\,.$ Mit $\sum$ als Summenzeichen.

Um den genauen Wert zu erhalten, wählt man die Wegstücke immer kleiner, so dass ihre Länge gegen null und ihre Anzahl gegen unendlich geht. Der Grenzwert der Summe ist das Weg- oder Kurvenintegral

$W=\int _{{{\vec s}_{1}}}^{{{\vec s}_{2}}}{\vec F}({\vec s})\cdot {\mathrm d}{\vec s}\,{\mathrm {,}}$

wobei ${\vec s}_{1}\,$ den Anfangspunkt und ${\vec s}_{2}\,$ den Endpunkt des Weges bezeichnen.

Mittels der Variablensubstitution ${\text{d}}{\vec {s}}={\vec {v}}\,{\text{d}}t$ lässt sich das Arbeitsintegral mit der Geschwindigkeit $\vec{v}(t)$ umschreiben zu

$W=\int _{t_{1}}^{t_{2}}{\vec {F}}({\vec {s}}(t))\,{\vec {v}}(t)\,{\text{d}}t$ .

Ist die Kraft ${\vec F}({\vec s})$ der Gradient eines Potentials

$\vec F(\vec s) = \nabla V(\vec s)\mathrm{,}$

dann handelt es sich um eine konservative Kraft. In diesem Fall hängt der Wert des Integrals – also die Arbeit – nur von dem Start- und dem Endpunkt ab, jedoch nicht von dem genauen Verlauf des Weges. Man kann die Arbeit in einem Potentialfeld also auch einfach durch die Differenz der potentiellen Energien berechnen:

$W=V({\vec s}_{2})-V({\vec s}_{1})$

Umgekehrt ist die potentielle Energie an einem bestimmten Ort gleich der Arbeit, die erforderlich ist, um den Probekörper von einem zuvor festgelegten Nullniveau dorthin zu bringen.

Handelt es sich bei dem Weg um eine geschlossene Kurve (sprich: sind der Start- und der Endpunkt identisch), dann ist die Arbeit null.

Dissipativen Kräften liegt jedoch kein Potenzialfeld zugrunde. Dies ist z.B. bei der Reibung der Fall. Hier kommt die Arbeit nicht der potenziellen oder kinetischen Energie des Probekörpers zugute, sondern der inneren Energie des Systems. Die Dissipation von Arbeit ist ein irreversibler Prozess. Dabei erhöht sich die Entropie des Systems, ohne dass Wärme von außen zugeführt wurde.

Kraftwandler und Goldene Regel der Mechanik

Will man eine bestimmte Arbeit mit geringerer Kraft leisten, so ist dies mit einem Kraftwandler möglich. Beispiele für Kraftwandler sind Flaschenzüge, Hebel oder Getriebe. Jedoch verlängert sich der Weg über den die Kraft aufgebracht werden muss. Wird beispielsweise durch Verwendung eines Kraftwandlers nur ein Viertel der ohne ihn erforderlichen Kraft benötigt, so ist dies mindestens mit einer Vervierfachung des Weges verbunden. Diese Konsequenz des Energieerhaltungssatzes beschreibt die „Goldene Regel der Mechanik“.

Beispiele

Hubarbeit: Arbeit, die an einem ruhenden Körper der Masse verrichtet werden muss, um ihn im homogenen Schwerefeld mit Erdbeschleunigung um die Hubhöhe zu heben

Die zum Heben benötigte Kraft beträgt (in Folge der Schwerkraft): $F=m\,g$ ,

Die zurückgelegte Strecke entspricht der Höhe .

Damit beträgt die geleistete Hubarbeit: $W_{H}=F\,s=m\,g\,h.$

Spannarbeit, auch Federarbeit, um eine zunächst ungespannte Feder um die Strecke zu dehnen:

Die (Spann-)Kraft einer Feder der Federkonstante beträgt bei der Federdehnung : $F(x)=D\,x$ .

Da die Kraft längs des Weges nicht konstant ist, tritt an Stelle des Produkts $W=F\,s$ das Integral $W=\int _{0}^{s}F(x)\,dx$ .

Damit beträgt die verrichtete Spannarbeit: $W_{S}=\int _{0}^{s}Dx\,dx={\frac {1}{2}}\,D\,s^{2}$ .

Beschleunigungsarbeit: Ein Körper der Masse wird auf eine Geschwindigkeit beschleunigt und dabei seine kinetische Energie um $\Delta E_{\text{kin}}$ geändert:

Aus der Ruhe:

$W_{B}=E_{\text{kin}}={\frac {1}{2}}\,m\,v^{2}\,.$

Oder allgemeiner von der Geschwindigkeit $v_{0}$ ausgehend:

$W_{B}=\Delta E_{\text{kin}}={\frac {1}{2}}\,m\,v^{2}-{\frac {1}{2}}\,m\,v_{0}^{2}={\frac {1}{2}}\,m\,(v^{2}-v_{0}^{2}).$

Kompressionsarbeit: Arbeit, die an einem Gas verrichtet werden muss, um es vom Volumen auf das Volumen zu verdichten:

$W=-\int _{{V_{1}}}^{{V_{2}}}p\,{\mathrm d}V.$

Das negative Vorzeichen stammt aus der Konvention, dass die von außen zugeführte Arbeit positiv zu werten ist. Der Druck kann (je nach Art der Zustandsänderung) variabel oder konstant sein.

Bei konstantem Druck wird daraus die Druck-Volumen-Arbeit, z.B. bei der Förderung eines Flüssigkeitsvolumens gegen einen konstanten Förderungshinderungsdruck.

$W_{{DV}}=p\,V\,.$

Elektrische Arbeit: Um die positive Ladungsmenge von einem Punkt zu einem anderen zu bewegen, zwischen welchen die Elektrische Spannung herrscht, muss die Arbeit

$W_{{\mathrm {el}}}=-\,Q\,U$

verrichtet werden. Hierbei ist das Vorzeichen der Spannung so gewählt worden, dass sie positiv ist, wenn das elektrische Potential am Anfang höher ist als am Ende.

Reibungsarbeit: Im einfachsten Fall, bei makroskopischen Körpern, definiert als Produkt aus Reibungskraft und Weg, also $W={\vec F}_{{\mathrm {Reib}}}\cdot {\vec s}$ . Allgemein wird hier mechanische Energie in Innere Energie umgewandelt. Siehe auch Dissipation.

Ein Beispiel aus der Physiologie: Die Herzarbeit setzt sich aus der Druck-Volumen-Arbeit und der Beschleunigungsarbeit durch Addition der Arbeit der beiden Ventrikel zusammen.

Historische Entwicklung

In den Anfängen der Mechanik wurde die Arbeit noch nicht von allen Gelehrten als Kraft mal Weg definiert. Stattdessen herrschte gut ein halbes Jahrhundert Verwirrung und Streit um die Frage, wie physikalische Arbeit zu bemessen sei. So standen sich im 17. Jahrhundert insbesondere Leibniz und Descartes mit ihren Ansichten stellvertretend gegenüber: Leibniz bevorzugte eine Vorform der heutigen Definition, in der die Arbeit proportional zum Weg ist - Descartes vertrat eine Proportionalität zur Zeit. Descartes Auffassung entsprach damit der alltäglichen Wahrnehmung des Arbeitsbegriffs; einer über eine bestimmte Zeit wirkenden Anstrengung.

Beide Auffassungen bestanden solange ungestört nebeneinander, wie lediglich die statischen Maschinen des Altertums betrachtet wurden (Hebel, Flaschenzug oder die schiefe Ebene). Bei diesen ist es unerheblich, ob die Goldene Regel der Mechanik auf den gesparten Weg oder die gesparte Zeit bezogen wird. Als Leibniz allerdings 1686 in den Acta Eruditorum den Vergleich beider Herangehensweisen bei einem Beispiel aus der Dynamik, dem Fallenlassen von Gewichten, anwandte, kam es zu Differenzen beider Parteien. Denn durch die seit Galilei bekannte quadratische Zunahme der Fallstrecke mit der Zeit, stimmen die Aufschlagsenergien zwischen den Definitionen nicht überein. Ein Gewicht, welches aus der vierfachen Höhe gegenüber einem Vergleichskörper fällt, besitzt nur die zweifache Fallzeit. Leibniz sprach ihm in den heutigen Begriffen daher vierfache Energie zu, Descartes und seine Anhänger nur doppelte.

Aufgrund der gewissen Willkürlichkeit, mit der sich sowohl der Fallstrecke als auch der Fallzeit die entscheidende Bedeutung für die freigewordene Arbeit zuweisen ließ, dauerte der Streit lange an und führte zu keiner wirklichen Klärung. Selbst Leibniz wurde mit der Zeit unsicher und äußerte, dass auch die Varianten "Kraft mal Zeit" bzw. "Masse mal Geschwindigkeit" mit Vorsicht für die Bestimmung von Bewegungsenergie genutzt werden könnten. Schlussendlich etablierte sich die heutige Proportionalität zwischen Arbeit und Weg.

Literatur

Christian Gerthsen, Dieter Meschede (Hrsg.): Physik. 23. Auflage. Springer Verlag, Berlin 2006, ISBN 3-540-25421-8.
Joachim Grehn (Hrsg.): Metzler Physik. 4. Auflage. Schroedel Schulbuchverlag, Hannover 2007, ISBN 978-3-507-10710-6.

Anmerkungen

↑ Diese Einheit ist nicht mit der Einheit des Drehmoments zu verwechseln, die auch Newtonmeter heißt. Drehmoment und Arbeit hängen über die Gleichung $W=M\varphi$ zusammen. Da der Winkel $\varphi$ eine Größe der Dimension Zahl ist, ist die Dimension von Arbeit und Drehmoment dieselbe, obwohl es sich um verschiedene Größenarten handelt.

Basierend auf einem Artikel in:

Wikipedia.de