Zyklische Gruppe

In der Gruppentheorie ist eine zyklische Gruppe eine Gruppe, die von einem einzelnen Element erzeugt wird. Sie besteht nur aus Potenzen des Erzeugers :

$\left\langle a \right\rangle := \lbrace a^n \mid n \in \Z \rbrace.$

Eine Gruppe ist also zyklisch, wenn sie ein Element enthält, sodass jedes Element von eine Potenz von ist. Gleichbedeutend damit ist, dass es ein Element gibt, sodass selbst die einzige Untergruppe von ist, die enthält. In diesem Fall wird ein erzeugendes Element oder kurz ein Erzeuger von genannt.

Zyklische Gruppen sind die einfachsten Gruppen und können vollständig klassifiziert werden: Für jede natürliche Zahl (für diese Aussage betrachten wir 0 nicht als natürliche Zahl) gibt es eine zyklische Gruppe $C_{n}$ mit genau Elementen, und es gibt die unendliche zyklische Gruppe, die additive Gruppe der ganzen Zahlen $\mathbb {Z}$ . Jede andere zyklische Gruppe ist zu einer dieser Gruppen isomorph.

Veranschaulichung

Drehgruppen

Die endlichen zyklischen Gruppen können veranschaulicht werden als Drehgruppen regulärer Vielecke in der Ebene. Zum Beispiel besteht die Gruppe $C_{4}$ aus den möglichen Drehungen der Ebene, die ein vorgegebenes Quadrat in sich überführen.

Drehungen, die ein Quadrat in sich überführen

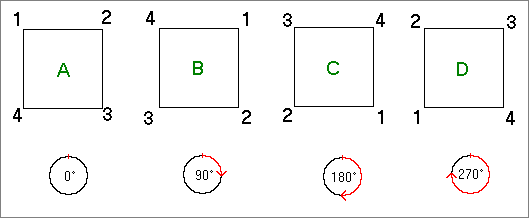
Die obenstehende Abbildung zeigt ein Quadrat A und die Stellungen B, C und D, in die es durch Drehen überführt werden kann. Darunter ist jeweils die dazu nötige Drehung angegeben. Die Elemente der zyklischen Gruppe sind hier die Bewegungen und nicht die Stellungen des Quadrats. Das heißt, die Gruppe $C_{4}$ besteht in dieser Darstellung aus der Menge {0°, 90°, 180°, 270°}. Die Verknüpfung der Elemente ist die Hintereinanderausführung der Drehungen; das entspricht einer Addition der Winkel. Dabei stimmt die Drehung um 360° mit der Drehung um 0° überein, die Winkel werden also genau genommen modulo 360° addiert.

Lässt man nicht nur Drehungen der Ebene zu, sondern auch Spiegelungen, dann erhält man im Fall von Vielecken die so genannten Diedergruppen.

Beachte auch, dass die Drehgruppe des Kreises, $S^{1}$ , nicht zyklisch ist.

Restklassengruppen

Eine andere Darstellung einer zyklischen Gruppe liefert die Addition modulo einer Zahl, die so genannte Restklassenarithmetik. In der additiven Gruppe $(\Z/n\Z, +)$ ist die Restklasse der 1 ein Erzeuger, das heißt, man kann jede andere Restklasse erhalten, indem man die 1 wiederholt mit sich selbst addiert. Am Beispiel $\Z/4\Z = \{0, 1, 2, 3\}$ bedeutet dies, dass sich alle 4 Elemente als Summe von 1 darstellen lassen, also 1 = 1, 2 = 1+1, 3 = 1+1+1, 0 = 1+1+1+1. Die Restklassengruppe $\Z/4\Z$ verhält sich genauso wie die oben beschriebene Drehgruppe {0°, 90°, 180°, 270°}: 0 entspricht 0°, 1 entspricht 90° usw: Diese beiden Gruppen sind isomorph.

Schreibweisen

Für endliche zyklische Gruppen gibt es im Wesentlichen drei Schreibweisen: $C_{n}$ , $\Z / n\Z$ und $\Z_n$ . Für nichtendliche zyklische Gruppen stehen die beiden Schreibweisen $C_\infty$ und $\mathbb {Z}$ zur Verfügung. Als Gruppenoperation wird in $C_{n}$ meist die Multiplikation und in $\mathbb {Z}$ , $\Z / n\Z$ und $\Z_n$ die Addition verwendet.

Die Schreibweisen $\Z / n\Z$ , $\Z_n$ und $\mathbb {Z}$ rühren daher, dass die additiven Gruppen der Restklassenringe $\Z/n\Z$ und von $\mathbb {Z}$ selbst die bekanntesten Vertreter zyklischer Gruppen sind. Im Gegensatz zur -Schreibweise verleiten sie jedoch dazu, das Vorhandensein einer Ringstruktur anzunehmen. Die Bezeichnung $\Z_n$ wird zudem auch noch im Zusammenhang mit p-adischen Zahlen verwendet.

Eigenschaften

Alle zyklischen Gruppen sind abelsche Gruppen.

Eine zyklische Gruppe kann mehrere Erzeuger haben. Die Erzeuger von $\mathbb {Z}$ sind +1 und -1, die Erzeuger von $\Z/n\Z$ sind die Restklassen, die teilerfremd zu sind; ihre Anzahl $\varphi(n)$ wird von der Eulerschen φ-Funktion angegeben.

Ist allgemein ein Teiler von , dann ist $\varphi(d)$ die Anzahl der Elemente von $\Z/n\Z$ , die die Ordnung haben:

$\Big| \{m \in \Z/n\Z \mid \text{ord}(m) = d\} \Big| = \varphi(d)$ .

Das direkte Produkt zweier zyklischer Gruppen $C_{n}$ und $C_{m}$ ist genau dann zyklisch, wenn und teilerfremd sind; in diesem Fall ist das Produkt isomorph zu $C_{mn}$ .

Jede endlich erzeugte abelsche Gruppe ist direktes Produkt endlich vieler endlicher und unendlicher zyklischer Gruppen.

Der Gruppenexponent einer endlichen zyklischen Gruppe ist gleich ihrer Ordnung. Jede endliche zyklische Gruppe ist isomorph zur additiven Gruppe des Restklassenring $\Z/n\Z$ , der Isomorphismus ist dabei der diskrete Logarithmus: Ist ein Erzeuger von $C_{n}$ , dann ist die Abbildung

$a^t \mapsto t$ mod

ein Isomorphismus.

Untergruppen und Faktorgruppen

Alle Untergruppen und Faktorgruppen von zyklischen Gruppen sind zyklisch. Insbesondere sind die Untergruppen von $\mathbb {Z}$ von der Form $m\Z$ mit einer natürlichen Zahl zyklisch. Alle diese Untergruppen sind verschieden, und für $m\not =0$ sind sie isomorph zu $\mathbb {Z}$ .

Der Verband der Untergruppen von $\mathbb {Z}$ ist isomorph zum dualen Verband der natürlichen Zahlen mit der Teilbarkeit. Alle Faktorgruppen von $\mathbb {Z}$ sind endlich, mit Ausnahme der trivialen Faktorgruppe $\Z/\{0\}$ .

Für jeden positiven Teiler von hat die Gruppe $\Z/n\Z$ genau eine Untergruppe der Ordnung , nämlich die von dem Element n/d erzeugte Untergruppe $\left\{kn/d\mid k=0,\ldots ,d-1\right\}$ . Andere als diese Untergruppen gibt es nicht. Der Untergruppenverband ist deshalb isomorph zum Teilerverband von .

Eine zyklische Gruppe ist genau dann einfach, wenn ihre Ordnung eine Primzahl ist.

Endomorphismen und Automorphismen

Der Endomorphismenring (siehe Gruppenhomomorphismus) der Gruppe $C_{n}$ ist Ring-isomorph zum Restklassenring $\Z/n\Z$ . Unter diesem Isomorphismus entspricht die Restklasse von $\Z/n\Z$ dem Endomorphismus von $C_{n}$ , der jedes Element auf seine -te Potenz abbildet. Daraus folgt, dass die Automorphismengruppe von $C_{n}$ isomorph zur Gruppe $(\Z/n\Z)^*$ , der Einheitengruppe des Rings $\Z/n\Z$ , ist. Diese Gruppe besteht aus den Elementen, die teilerfremd zu sind, und hat somit genau $\phi (n)$ Elemente.

Der Endomorphismenring der zyklischen Gruppe $\mathbb {Z}$ ist isomorph zum Ring $\mathbb {Z}$ , und die Automorphismengruppe ist isomorph zur Einheitengruppe $\left\{+1,-1\right\}$ von $\mathbb {Z}$ , und diese ist isomorph zur zyklischen Gruppe $C_{2}$ .

Algebraische Eigenschaften

Ist eine natürliche Zahl, dann ist $(\Z/n\Z)^*$ genau dann zyklisch, wenn gleich 2, 4, $p^{k}$ oder 2p^k ist, für eine Primzahl p>2 und eine natürliche Zahl . Die Erzeuger dieser zyklischen Gruppe heißen Primitivwurzeln modulo .

Insbesondere ist für jede Primzahl die Gruppe $(\Z/p\Z)^*$ zyklisch mit -1 Elementen. Allgemeiner ist jede endliche Untergruppe der multiplikativen Gruppe eines Körpers zyklisch.

Die Galoisgruppe einer endlichen Körpererweiterung eines endlichen Körpers ist eine endliche zyklische Gruppe. Umgekehrt gibt es für jeden endlichen Körper und jede endliche zyklische Gruppe eine endliche Körpererweiterung L/K mit Galoisgruppe .

Siehe auch

Basierend auf einem Artikel in:

Wikipedia.de