Distribution (Mathematik)

Eine Distribution bezeichnet im Bereich der Mathematik eine besondere Art eines Funktionals, also ein Objekt aus der Funktionalanalysis.

Die Theorie der Distributionen ermöglicht es, eine Art von Lösungen für Differentialgleichungen zu definieren, die im klassischen Sinn nicht hinreichend oft differenzierbar oder gar nicht definiert sind. In diesem Sinne können Distributionen als eine Verallgemeinerung des Begriffs der Funktion angesehen werden. Es gibt partielle Differentialgleichungen, die keine klassischen Lösungen, aber Lösungen im distributionellen Sinn haben. Die Theorie der Distributionen ist daher insbesondere in der Physik und in den Ingenieurwissenschaften wichtig: Viele der dort untersuchten Probleme führen nämlich zu Differentialgleichungen, die nur mit Hilfe der Theorie der Distributionen gelöst werden konnten.

Der Mathematiker Laurent Schwartz war maßgeblich an der Untersuchung der Theorie der Distributionen beteiligt. Im Jahr 1950 veröffentlichte er den ersten systematischen Zugang zu dieser Theorie. Für seine Arbeiten über die Distributionen erhielt er die Fields-Medaille.

Geschichte der Distributionentheorie

Jacques Hadamard

Im Jahr 1903 führte Jacques Hadamard den für die Distributionentheorie zentralen Begriff des Funktionals ein. Aus heutiger Sicht ist ein Funktional eine Funktion, die anderen Funktionen eine Zahl zuordnet. Hadamard konnte zeigen, dass jedes stetige, lineare Funktional als Grenzwert einer Folge von Integralen

$T(f)=\lim _{{n\to \infty }}\int f(t)g_{n}(t){\mathrm {d}}t$

Paul Dirac, 1933

dargestellt werden kann. In dieser Darstellung dürfen Grenzwert und Integral im Allgemeinen nicht vertauscht werden. Im Jahr 1910 konnte gezeigt werden, dass jedes stetige, lineare Funktional auf $L^{p}$ , dem Raum der p-integrierbaren Funktionen, als

$T(f)=\int f(x)g(x){\mathrm {d}}x$

mit $g\in L^{q}$ und $\tfrac{1}{p} + \tfrac{1}{q} = 1$ dargestellt werden kann. Bei dieser Formulierung muss kein Grenzwert gebildet werden und ist eindeutig bestimmt. Deshalb wird das Funktional oft mit der „Funktion“ identifiziert. Dann hat zwei unterschiedliche Bedeutungen: Zum einen versteht man als $L^{q}$ -„Funktion“, zum anderen wird es mit dem Funktional gleichgesetzt.

Als erster beschäftigte sich Paul Dirac in den 1920er Jahren bei Forschungen in der Quantenmechanik mit Distributionen. Er führte dabei die wichtige Delta-Distribution ein. Jedoch benutzte er noch keine mathematisch präzise Definition für diese Distribution. Er ließ bei seinen Untersuchungen die damalige Funktionalanalysis, also die Theorie der Funktionale, außer Acht. In den 1930er Jahren beschäftigte sich Sergei Lwowitsch Sobolew mit Anfangswertproblemen bei partiellen hyperbolischen Differentialgleichungen. Für diese Untersuchungen führte er die heute nach ihm benannten Sobolew-Räume ein. Im Jahr 1936 untersuchte Sobolew hyperbolische Differentialgleichungen zweiter Ordnung mit analytischen Koeffizientenfunktionen. Um ein griffigeres Kriterium für die Existenz einer Lösung dieser partiellen Differentialgleichung angeben zu können, erweiterte Sobolew die Fragestellung auf den Raum der Funktionale. Damit war er der erste, der die heutige Definition einer Distribution formulierte. Er entwickelte allerdings noch keine umfassende Theorie aus seinen Definitionen, sondern verwendete sie nur als Hilfsmittel zur Untersuchung partieller Differentialgleichungen.

Laurent Schwartz, 1970

Schließlich entwickelte Laurent Schwartz die Theorie der Distributionen im Winter 1944/45. Zu diesem Zeitpunkt waren ihm Sobolews Arbeiten noch unbekannt, doch stieß auch er genau wie Sobolew durch Fragen im Bereich der partiellen Differentialgleichungen auf spezielle Funktionale, die er nun Distributionen nannte. Von da an wurde die Theorie derart schnell weiterentwickelt, dass Schwartz darüber schon im Winter 1945/46 Vorlesungen in Paris halten konnte. Elektrotechniker, die seine Vorlesungen besuchten, drängten ihn dazu, seine Theorie in Richtung der Fourier- und der Laplacetransformationen weiterzuentwickeln. Im Jahr 1947 hatte Schwartz den Raum der temperierten Distributionen definiert und damit die Fourier-Transformationen in seine Theorie integriert. 1950/51 erschien seine Monografie Theorie des Distributions, wodurch seine Theorie weiter gefestigt wurde. Schon 1950 erhielt er für seine Forschungen im Bereich der Distributionen die Fields-Medaille, eine der höchsten Auszeichnungen im Bereich der Mathematik.

Die Theorie der Distributionen wurde von da an in der theoretischen Physik und in der Theorie der partiellen Differentialgleichungen weiterentwickelt. Die Distributionentheorie ist nützlich, um singuläre Objekte der Physik wie zum Beispiel die elektromagnetische Punktladung oder die Punktmasse mathematisch präzise zu beschreiben. Diese beiden physikalischen Objekte können mit Hilfe der Delta-Distribution geeignet beschrieben werden, denn von der räumlichen Dichtefunktion eines Massenpunktes mit Einheitsmasse wird gefordert, dass sie überall verschwindet, außer an einem Punkt. Dort muss sie unendlich werden, da das Raumintegral über die Dichtefunktion 1 ergeben soll (Einheitsmasse). Es gibt keine Funktion im üblichen Sinn, die diese Forderungen erfüllt. In der Theorie der partiellen Differentialgleichungen und der Fourieranalyse sind Distributionen wichtig, da mit dieser Begriffsbildung jeder lokal integrierbaren Funktion eine Ableitung zugeordnet werden kann.

Definitionen

Distribution

Sei $\Omega \subset \mathbb {R} ^{n}$ eine offene, nichtleere Menge. Eine Distribution ist ein stetiges und lineares Funktional auf dem Raum der Testfunktionen ${\mathcal {D}}(\Omega )$ .

In anderen Worten eine Abbildung $T\colon {\mathcal {D}}(\Omega )\to \mathbb {C}$ bzw. $T\colon {\mathcal {D}}(\Omega )\to \mathbb {R}$ , so dass für alle $\phi _{1},\phi _{2}\in {\mathcal {D}}(\Omega )$ und $\lambda \in \mathbb {C}$ gilt

$T(\phi _{1}+\lambda \phi _{2})=T(\phi _{1})+\lambda T(\phi _{2})$

und

$T(\phi _{n})\to T(\phi )$

wann immer $\phi _{n}\to \phi$ in ${\mathcal {D}}(\Omega )$ .

Raum der Distributionen

Die Menge der Distributionen ist mit den entsprechenden Verknüpfungen der Addition und der Skalarmultiplikation also der topologische Dualraum zum Testfunktionenraum ${\mathcal {D}}$ und wird daher als ${\mathcal {D}}'$ notiert. Das Zeichen bezeichnet in der Funktionalanalysis den topologischen Dualraum. Um überhaupt von Stetigkeit und topologischem Dualraum sprechen zu können, muss der Raum der Testfunktionen mit einer lokalkonvexen Topologie ausgestattet sein.

Oft verwendet man daher die folgende Charakterisierung als alternative Definition, da diese ohne die Topologie des Testfunktionenraums auskommt und kein Wissen über lokalkonvexe Räume erforderlich ist:

Sei $\Omega \subset \mathbb {R} ^{n}$ eine offene Menge. Ein lineares Funktional $T\colon {\mathcal {D}}(\Omega )\to \mathbb {C}$ heißt Distribution, wenn für jedes Kompaktum $K \subset \Omega$ ein C>0 und ein $k \in \N_0$ existieren, sodass für alle Testfunktionen $\phi \in {\mathcal {D}}(K)$ die Ungleichung

$|T(\phi )|\leq C\|\phi \|_{{C_{b}^{k}(K)}}:=C\sum _{{|\alpha |\leq k}}^{{}}\sup _{{x\in K}}\left|\partial ^{\alpha }\phi (x)\right|$

gilt. Diese Definition ist äquivalent zu der zuvor gegebenen, denn die Stetigkeit des Funktionals folgt aus dieser Ungleichung, obwohl sie nicht für ganz $\Omega$ gelten muss, weil ${\mathcal {D}}(\Omega )$ als (LF)-Raum bornologisch ist.

Ordnung einer Distribution

Kann in der obigen alternativen Definition für alle Kompakta dieselbe Zahl gewählt werden, so wird das kleinstmögliche als Ordnung von bezeichnet. Die Menge der Distributionen der Ordnung wird mit ${\mathcal {D}}'^{k}(\Omega )$ bezeichnet und mit $\textstyle {\mathcal {D}}'_{F}(\Omega ):=\bigcup _{{k}}{\mathcal {D}}'^{k}(\Omega )$ notiert man die Menge aller Distributionen mit endlicher Ordnung. Dieser Raum ist kleiner als der allgemeine Distributionenraum ${\mathcal {D}}'(\Omega )$ , denn es gibt auch Distributionen, die nicht von endlicher Ordnung sind.

Reguläre Distribution

Eine besondere Teilmenge der Distributionen sind die regulären Distributionen. Diese Distributionen werden durch eine lokal integrierbare Funktion $f\in L_{\mathrm {loc} }^{1}(\mathbb {R} ^{n})$ erzeugt. Präzise bedeutet dies, dass eine Distribution regulär genannt wird, wenn es eine Darstellung

$T_{f}(\phi )=\int _{\mathbb {R} ^{n}}f(t)\phi (t)\mathrm {d} t$

gibt, bei der $f\in L_{{\mathrm {loc}}}^{1}(\mathbb{R} ^{n})$ eine lokal integrierbare Funktion ist. Nichtreguläre Distributionen werden auch singulär genannt; das sind Distributionen, für die es keine erzeugende Funktion im Sinn dieser Definition gibt.

Diese Integraldarstellung einer regulären Distribution motiviert zusammen mit dem Skalarprodukt im $\mathbb {R} ^{n}$ die alternative Schreibweise

$(T,\phi ):=T(\phi )$

für alle (nicht nur reguläre) Distributionen.

Testfunktionen

→ Hauptartikel: Testfunktion

In der Definition der Distribution ist der Begriff der Testfunktion beziehungsweise der des Testfunktionenraums zentral. Dieser Testfunktionenraum ist der Raum der glatten Funktionen mit kompaktem Träger zusammen mit einer induzierten Topologie. Eine Topologie auf dem Testfunktionenraum zu wählen ist sehr wichtig, weil sonst der Begriff der Stetigkeit nicht sinnvoll definiert werden kann. Die Topologie wird auf dem Raum durch einen Konvergenzbegriff festgelegt.

Sei $\Omega \subset \mathbb {R} ^{n}$ eine offene Teilmenge, dann bezeichnet

$C_{c}^{\infty }(\Omega )=\{\phi \in C^{\infty }(\Omega )\mid \operatorname {supp} \,(\phi )\mathrm {~ist~kompakte~Teilmenge~von~} \Omega \}$

die Menge aller unendlich oft differenzierbaren Funktionen, die einen kompakten Träger haben, also außerhalb einer kompakten Menge gleich null sind. Der Konvergenzbegriff wird festgelegt, indem man definiert: Eine Folge $(\phi _{j})_{j\in \mathbb {N} }$ mit $\phi _{j}\in C_{c}^{\infty }(\Omega )$ konvergiert gegen ${\phi }$ , wenn es ein Kompaktum $K \subset \Omega$ gibt mit $\operatorname {supp} (\phi _{j})\subset K$ für alle und

$\lim _{{j\rightarrow \infty }}\sup _{{x\in K}}\left|{\frac {\partial ^{\alpha }}{\partial x^{\alpha }}}\left(\phi _{j}(x)-\phi (x)\right)\right|=0$

für alle Multiindizes $\alpha \in \N^n$ . Die Menge $C_c^\infty(\Omega)$ ist – ausgestattet mit diesem Konvergenzbegriff – ein lokalkonvexer Raum, den man Raum der Testfunktionen nennt und als ${{\mathcal D}}(\Omega )$ notiert.

Zwei unterschiedliche Sichtweisen

Wie weiter oben im Abschnitt zur Definition der Distribution beschrieben, ist eine Distribution ein Funktional, also eine Funktion mit bestimmten Zusatzeigenschaften. Im Abschnitt Geschichte der Distributionentheorie wurde dagegen gesagt, dass die Delta-Distribution keine Funktion sein kann. Dies ist offensichtlich ein Widerspruch, der sich auch in der aktuellen Literatur noch wiederfindet. Dieser Widerspruch entsteht dadurch, dass versucht wird, Distributionen – und auch Funktionale auf $L^{p}$ -Räumen – mit reellwertigen Funktionen zu identifizieren.

Insbesondere in der theoretischen Physik versteht man unter einer Distribution ein Objekt, beispielsweise $\delta$ genannt, mit gewissen sich aus dem Kontext ergebenden Eigenschaften. Die gewünschten Eigenschaften verhindern oft, dass $\delta$ eine Funktion sein kann, aus diesem Grund spricht man dann von einer verallgemeinerten Funktion. Nachdem nun die Eigenschaften von $\delta$ festgelegt sind, betrachtet man die Zuordnung

$C_c^{\infty}(\Omega) \ni \phi \mapsto \int \delta(x) \phi(x) \mathrm{d}x \in \mathbb{R},$

die einer Testfunktion ${\phi }$ eine reelle Zahl zuordnet. Da $\delta$ jedoch im Allgemeinen keine Funktion ist, muss für den Ausdruck von Fall zu Fall erst ein Sinn erklärt werden.

Mathematisch gesehen ist eine Distribution eine Funktion mit bestimmten abstrakten Eigenschaften (Linearität und Stetigkeit), die einer Testfunktion eine reelle Zahl zuordnet. Ist das $\delta$ aus vorigem Absatz eine integrierbare Funktion, so ist der Ausdruck $\textstyle T(\phi )=\int \delta (x)\phi (x){\mathrm {d}}x$ mathematisch präzise definiert. Jedoch wird hier nicht die Funktion $\delta$ als Distribution bezeichnet, sondern das Funktional $\textstyle \int \delta (x)\cdot {\mathrm {d}}x$ heißt Distribution.

Auch viele Mathematiklehrbücher unterscheiden nicht zwischen der (distributions-) erzeugenden Funktion $\delta$ und der eigentlichen Distribution im mathematischen Sinne. In diesem Artikel wird vorwiegend die strengere mathematische Sichtweise verwendet.

Beispiele

Stetige Funktion als Erzeuger

Sei $\Omega \subseteq \mathbb{R}$ und $f\in C(\Omega )$ , so ist durch

$T(\phi ):=\int _{-\infty }^{\infty }f(x)\phi (x)\mathrm {d} x$

für alle $\phi \in C_{c}^{\infty }(\Omega )$ eine Distribution $T\in {\mathcal {D}}'(\Omega )$ definiert.

Delta-Distribution

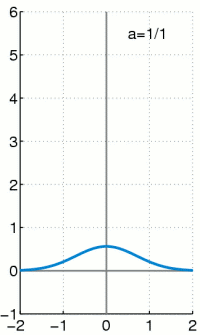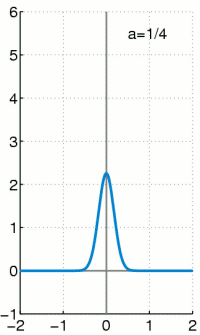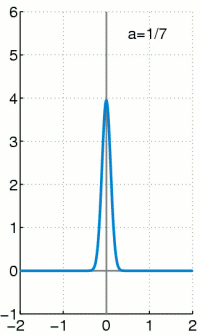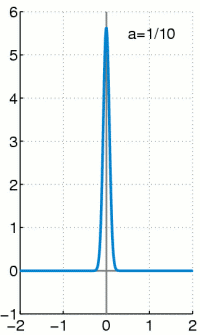
Die Delta-Distribution wird durch die Funktionenfolge $\textstyle \delta _{{a}}(x)={\frac {1}{{\sqrt {2\pi a}}}}\cdot e^{{-{\frac {x^{2}}{2a}}}}$ approximiert. Für alle bleibt der Flächeninhalt unter der Funktion gleich Eins.

→ Hauptartikel: Delta-Distribution

Die Delta-Distribution $\delta$ ist eine singuläre Distribution. Das heißt, sie kann nicht durch eine gewöhnliche Funktion erzeugt werden, obwohl sie oft wie eine solche geschrieben wird. Es gilt:

$\delta (\phi ):=\phi (0).$

Das heißt, die Delta-Distribution angewendet auf eine Testfunktion ${\phi }$ ergibt den Wert der Testfunktion an der Stelle 0. So wie jede andere Distribution kann man auch die Delta-Distribution als Folge von Integraltermen ausdrücken. Die Dirac-Folge

$\delta _{{a}}(x)={\frac {1}{{\sqrt {2\pi a}}}}\cdot e^{{-{\frac {x^{2}}{2a}}}}$

hat den Grenzwert (vergleiche z.B. die nebenstehende Animation)

${{\mathrm {Gw}}}(x):=\lim _{{a\to 0}}\delta _{{a}}(x)={\begin{cases}0&x\neq 0\\\infty &x=0\end{cases}}\,,$

was zu dem verschwindenden Integral $\textstyle \int _{{\mathbb{R} }}{{\rm {{Gw}}}}(x){{\rm {d}}}x=0$ führen würde. Denn das Verhalten in nur einem Punkt fällt bei Integralen gewöhnlicher Funktionen nicht ins Gewicht.

Mit dieser Dirac-Folge kann man aber mit anderer Grenzwertbildung, vor dem Integral und nicht dahinter, die Delta-Distribution durch

$\delta (\phi )=\lim _{{a\to 0}}\int _{{\mathbb{R} }}\delta _{a}(x)\phi (x){\mathrm {d}}x=\lim _{{a\to 0}}\int _{{\mathbb{R} }}{\tfrac {1}{{\sqrt {2\pi a}}}}\cdot e^{{-{\frac {x^{2}}{2a}}}}\phi (x){\mathrm {d}}x=\phi (0)$

darstellen. Meistens wird allerdings die symbolische, zu mathematisch unpräziser Interpretation verleitende Schreibweise

$\delta (\phi )=\int _{\mathbb{R} }\delta (x)\phi (x){\mathrm {d}}x=\phi (0)$

für die Delta-Distribution verwendet, wobei man den Ausdruck $\delta (x)$ als verallgemeinerte Funktion bezeichnet und oft sogar das Wort verallgemeinert weglässt.

Dirac-Kamm

Dirac-Kamm

→ Hauptartikel: Dirac-Kamm

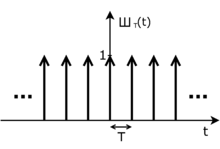
Der Dirac-Kamm $\Delta _{T}$ mit $T\in {\mathbb {R}}$ ist eine periodische Distribution, die mit der diracschen Delta-Distribution eng verwandt ist. Diese Distribution ist für alle $\phi \in {\mathcal {D}}(\mathbb{R} )$ definiert als

$\Delta _{T}(\phi ):=\sum _{n\in \mathbb {Z} }\phi (nT).$

Diese Reihe konvergiert, da die Testfunktion ${\phi }$ kompakten Träger hat und daher nur endlich viele Summanden ungleich null sind. Eine äquivalente Definition ist

$\Delta _{T}=\sum _{{n\in {\mathbb Z}}}\delta _{{nT}},$

wobei das Gleichheitszeichen als Gleichheit zwischen Distributionen zu verstehen ist. Die Reihe auf der rechten Seite konvergiert dann bezüglich der Schwach-*-Topologie. Auf die Konvergenz von Distributionen wird im Abschnitt Konvergenz näher eingegangen. Das in der Definition auftretende ist eine reelle Zahl, die man als Periode des Dirac-Kamms bezeichnet. Anschaulich ist der Dirac-Kamm also aus unendlich vielen Delta-Distributionen zusammengesetzt, die im Abstand zueinander stehen. Der Dirac-Kamm hat im Gegensatz zur Delta-Distribution keinen kompakten Träger. Was dies genau bedeutet, wird im Abschnitt Kompakter Träger weiter unten erklärt.

Radon-Maße

→ Hauptartikel: Radon-Maß

Mit $M(\Omega )$ wird die Menge aller Radon-Maße bezeichnet. Sei $\mu \in M(\Omega ).$ Nun kann man mittels

$\mu \mapsto \left(\phi \in {\mathcal {D}}(\Omega )\mapsto \int _{\Omega }\phi (x)\mathrm {d} \mu (x)\right)$

jedem $\mu$ eine Distribution zuordnen. Auf diese Weise kann man $M(\Omega )$ stetig in ${\mathcal {D}}'(\Omega )$ einbetten. Ein Beispiel für ein Radon-Maß ist das Dirac-Maß $\delta$ . Für alle $A\subset \Omega$ ist es definiert durch

$\delta (A):={\begin{cases}1\ ,&{\text{falls }}0\in A\ ,\\0\ ,&\mathrm {sonst} \ .\end{cases}}$

Identifiziert man das Dirac-Maß mit der erzeugenden Distribution

$\phi \in {\mathcal {D}}(\Omega )\mapsto \int _{\Omega }\phi (x){\mathrm {d}}\delta (x)=\phi (0),$

so erhält man die Delta-Distribution, falls $0\in \Omega \subset \mathbb{R} ^{n}$ gilt.

Cauchyscher Hauptwert von 1 / x

Die Funktion $x\mapsto 1/x$

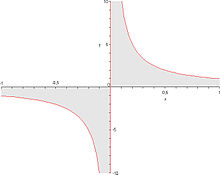
Der cauchysche Hauptwert der Funktion $\textstyle x\mapsto {\frac {1}{x}}$ kann ebenfalls als Distribution $T\in {\mathcal {D}}'(\mathbb{R} )$ aufgefasst werden. Für alle $\phi \in {\mathcal {D}}(\mathbb{R} )$ setzt man

${\begin{aligned}T(\phi )&:={\text{PV}}\int _{-\infty }^{\infty }{\frac {\phi (x)}{x}}\mathrm {d} x\\&:=\lim _{\varepsilon \to 0}\left(\int _{-\infty }^{-\varepsilon }{\frac {\phi (x)}{x}}\mathrm {d} x+\int _{\varepsilon }^{\infty }{\frac {\phi (x)}{x}}\mathrm {d} x\right).\end{aligned}}$

Das ist eine singuläre Distribution, da der Integralausdruck im lebesgueschen Sinn nicht definiert ist und nur als cauchyscher Hauptwert existiert. Dabei steht die Abkürzung PV für principal value.

Diese Distribution wird meist zusammen mit der Dispersionsrelation $\textstyle \lim _{\varepsilon \to 0^{+}}{\tfrac {1}{x-\mathrm {i} \varepsilon }}\,=\,{\rm {PV}}({\tfrac {1}{x}})+\mathrm {i} \pi \delta (x)$ (Plemelj-Sokhotsky-Formel) benutzt, wobei alle Distributionen, insbesondere $\delta (\phi )$ und $T(\phi ),$ wie angegeben durch verallgemeinerte Funktionen ausgedrückt sind und $\mathrm {i}$ die imaginäre Einheit bezeichnet. Diese Beziehung verbindet in der linearen Antworttheorie Real- und Imaginärteil einer Antwortfunktion, siehe Kramers-Kronig-Beziehungen. (An dieser Stelle wird angenommen, dass die Testfunktionen $\phi$ komplex sind, also $\phi \in \mathbb {C}$ , und auch die gerade angesprochenen Antwortfunktionen; aber das Argument soll nach wie vor reell sein, obwohl natürlich $x-\mathrm {i} \varepsilon$ komplex ist, und nicht reell.)

Oszillierendes Integral

Für alle Symbole $a\in S_{{1,0}}^{m}(\Omega \times \mathbb{R} ^{n})$ nennt man

$I(a)(x):=\int _{{\mathbb{R} ^{n}}}e^{{i\langle x,\xi \rangle }}a(x,\xi ){\mathrm {d}}\xi$

ein oszillierendes Integral. Dieser Integraltyp konvergiert je nach Wahl von nicht im Riemann- oder Lebesguesinn, sondern nur im Sinn von Distributionen.

Konvergenz

Da der Distributionenraum als topologischer Dualraum definiert ist, trägt er ebenfalls eine Topologie. Als Dualraum eines Montelraums, versehen mit der starken Topologie, ist er selber ein Montelraum, daher fällt für Folgen die starke Topologie mit der Schwach-*-Topologie zusammen. Für Folgen entsteht also folgender Konvergenzbegriff: Eine Folge $(T_{n})_{{n\in \mathbb{N} }}$ von Distributionen konvergiert gegen $T\in {\mathcal {D}}'(\Omega )$ , wenn für jede Testfunktion $\phi \in {\mathcal {D}}(\Omega )$ die Gleichung

$\lim _{{j\to \infty }}T_{j}(\phi )=T(\phi )$

gilt.

Weil jede Testfunktion $f\in {\mathcal {D}}(\Omega )$ mit $\textstyle T_{f}(\phi ):=\int _{\Omega }f(x)\phi (x)\mathrm {d} x$ identifiziert werden kann, kann ${\mathcal {D}}(\Omega )$ als ein topologischer Teilraum von ${\mathcal {D}}'(\Omega )$ aufgefasst werden.

Der Raum ${\mathcal {D}}(\Omega )$ liegt dicht in ${\mathcal {D}}'(\Omega )$ . Das bedeutet, dass für jede Distribution $T\in {\mathcal {D}}'(\Omega )$ eine Folge von Testfunktionen $(T_{j})_{{j\in \mathbb{N} }}$ in ${\mathcal {D}}(\Omega )$ mit $\textstyle \lim _{{j\to \infty }}T_{j}=T$ in ${\mathcal {D}}'(\Omega )$ existiert. Man kann also jede Distribution durch

$T(\phi )=\lim _{{j\to \infty }}\int _{{\Omega }}T_{j}(x)\phi (x){\mathrm {d}}x$

darstellen.

Lokalisierung

Einschränkung auf eine Teilmenge

Seien $Y\subset \Omega \subset \mathbb{R} ^{n}$ offene Teilmengen und sei $T\in {\mathcal {D}}'(\Omega )$ eine Distribution. Die Einschränkung $T|_{Y}$ von auf die Teilmenge ist definiert durch

$T|_{Y}(\phi )\colon =T({\tilde {\phi }})$

für alle $\phi \in {\mathcal {D}}(Y)$ , wobei ${\tilde {\phi }}\in {\mathcal {D}}(\Omega )$ das auf $\Omega \setminus Y$ durch null fortgesetzte $\phi$ ist.

Träger

Sei $T\in {\mathcal {D}}'(\Omega )$ eine Distribution. Man sagt, dass ein Punkt $x_{0}\in \Omega$ zum Träger von gehört und schreibt $x_{0}\in {\mathrm {supp}}(T)$ , wenn für jede offene Umgebung $U\subset \Omega$ von $x_{0}$ eine Funktion $\phi \in {\mathcal {D}}(U)$ existiert mit $T(\phi )\neq 0$ .

Falls eine reguläre Distribution $T=T_{f}$ mit stetigem ist, so ist diese Definition äquivalent zur Definition des Trägers einer Funktion (der Funktion ).

Kompakter Träger

Eine Distribution $T\in {\mathcal {D}}'(\Omega )$ hat einen kompakten Träger, wenn ${\mathrm {supp}}(T)$ ein kompakter Raum ist. Die Menge der Distributionen mit kompaktem Träger wird mit ${\mathcal {E}}'$ bezeichnet. Sie ist ein Untervektorraum von ${\mathcal {D}}'$ und der topologische Dualraum zu ${\mathcal {E}}$ , dem Raum der glatten Funktionen $C^{\infty }$ . Auf diesem Raum wird durch die Familie von Halbnormen

$\phi \mapsto \sum _{|\alpha |\leq m}\sup _{x\in K}\left|{\frac {\partial ^{\alpha }}{\partial x^{\alpha }}}\phi (x)\right|$ ,

wobei beliebige Werte aus $\mathbb {N}$ annimmt und alle kompakten Teilmengen des $\mathbb {R} ^{n}$ durchläuft, eine lokalkonvexe Topologie erzeugt.

Singulärer Träger

Sei $T\in {\mathcal {D}}'(\Omega )$ eine Distribution. Man sagt, dass ein Punkt $x_{0}\in \Omega$ nicht zum singulären Träger ${\mathrm {sing\,supp}}(T)$ gehört, wenn es eine offene Umgebung $U\subset \Omega$ von $x_{0}$ und eine Funktion $f\in C^{\infty }(U)$ gibt mit

$T(\phi )=\int _{U}f(x)\phi (x)\mathrm {d} x$

für alle $\phi \in C_{c}^{\infty }(U)$ .

Anders gesagt: $x_{0}\in {\mathrm {sing\,supp}}(T)$ genau dann, wenn es keine offene Umgebung von $x_{0}$ gibt, sodass die Einschränkung von auf gleich einer glatten Funktion ist. Insbesondere ist der singuläre Träger einer singulären Distribution nicht leer.

Operationen auf Distributionen

Da der Distributionenraum mit punktweiser Addition und Multiplikation mit komplexen Zahlen ein Vektorraum über dem Körper $\mathbb {C}$ ist, sind die Addition von Distributionen und die Multiplikation einer komplexen Zahl mit einer Distribution schon definiert.

Im Folgenden werden weitere Operationen auf Distributionen wie die Ableitung einer Distribution erklärt. Viele Operationen werden auf Distributionen übertragen, indem die entsprechende Operation auf die Testfunktionen angewendet wird. Ist zum Beispiel $L\colon {\mathcal D}(\Omega _{1})\to L_{{\text{loc}}}^{1}(\Omega _{2})$ eine lineare Abbildung, die eine $D(\Omega _{1})$ -Testfunktion auf eine $L_{{\text{loc}}}^{1}(\Omega _{2})$ -Funktion abbildet, und existiert außerdem noch eine adjungierte lineare und folgenstetige Abbildung $L^{*}\colon {\mathcal D}(\Omega _{2})\to {\mathcal D}(\Omega _{1})$ , sodass für alle Testfunktionen $\varphi \in {\mathcal D}(\Omega _{1})$ und $\psi \in {\mathcal D}(\Omega _{2})$ gilt

$\int _{\Omega _{1}}\varphi (x)(L^{*}\psi )(x)\mathrm {d} x=\int _{\Omega _{2}}(L\varphi )(x)\psi (x)\mathrm {d} x$ ,

dann ist

${\tilde L}\colon {\mathcal D}'(\Omega _{1})\to {\mathcal D}'(\Omega _{2}){\text{, }}{\tilde L}(u)(\varphi )=u(L^{*}\varphi )$

eine wohldefinierte Operation auf Distributionen.

Multiplikation mit einer Funktion

Sei $T\in {\mathcal {D}}'(\Omega )$ und $a\in C^{\infty }(\Omega )$ . Dann wird die Distribution $aT\in {\mathcal {D}}'(\Omega )$ definiert durch

$\forall \phi \in {\mathcal {D}}(\Omega )\colon (aT)(\phi ):=T(a\phi )$ .

Differentiation

Motivation

Betrachtet man eine stetig differenzierbare Funktion und die ihr zugeordnete reguläre Distribution $T_{f}$ , so erhält man die Rechenregel

${\begin{aligned}(T_{f^{\prime }},\varphi )&=\int _{\Omega }f^{\prime }(t)\varphi (t)\,\mathrm {d} t\\&=-\int _{\Omega }f(t)\varphi ^{\prime }(t)\,\mathrm {d} t\\&=-(T_{f},\varphi ^{\prime }).\end{aligned}}$

Hierbei wurde partielle Integration verwendet, wobei die Randterme wegen der gewählten Eigenschaften der Testfunktion $\varphi$ wegfallen. Dies entspricht der schwachen Ableitung. Die beiden äußeren Terme sind auch für singuläre Distributionen definiert. Man verwendet dies zur Definition der Ableitung einer beliebigen Distribution .

Definition

Sei also $T\in {\mathcal {D}}'(\Omega )$ eine Distribution, $\alpha \in \N^n$ ein Multiindex und $x\in \Omega$ . Dann ist die Distributionsableitung $\partial _{x}^{\alpha }T\in {\mathcal {D}}'(\Omega )$ definiert durch

$(\partial _{x}^{\alpha }T)(\phi ):=(-1)^{|\alpha |}T(\partial _{x}^{\alpha }\phi ),\quad \forall \phi \in {\mathcal {D}}(\Omega )$ .

Im eindimensionalen Fall bedeutet dies gerade

$T'(\varphi )=-T(\varphi ')$ .

Häufig verwendet man für die Distributionsableitung auch die Notation $D^{\alpha }T$ .

Beispiel

Die Heaviside-Funktion $H\colon \mathbb {R} \to \mathbb {R}$ ist durch

$H(x)={\begin{cases}0:&x\leq 0,\\1:&x>0,\end{cases}}$

definiert. Sie ist mit Ausnahme der Stelle x=0 überall differenzierbar. Man kann sie als reguläre Distribution betrachten und die Rechnung

${\begin{aligned}(H^{\prime },\phi )&=-(H,\phi ^{\prime })\\&=-\int _{0}^{\infty }1\cdot \phi ^{\prime }(x)\,\mathrm {d} x\\&=\phi (0)\\&=(\delta ,\phi )\end{aligned}}$

zeigt, dass ihre Ableitung (als Distribution) die Delta-Distribution ist:

$H^{\prime }=\delta .$

Man kann außerdem die Delta-Distribution selbst ableiten:

$\left(\delta ^{(n)},\phi \right)=(-1)^{n}\left(\delta ,\phi ^{(n)}\right)=(-1)^{n}\phi ^{(n)}(0)$

Die Ableitungen der Delta-Distribution sind also bis auf den zusätzlichen Vorzeichenfaktor $(-1)^{n}$ gleich den Ableitungen der Testfunktion an der Stelle $x=0.$

Tensorprodukt

Motivation

Sei die Menge $G\subset \mathbb{R} ^{{2n}}$ als Produktraum $G:=G_{1}\times G_{2}$ mit $G_{1},G_{2}\subset \mathbb{R} ^{n}$ gegeben. Dann kann man auf den Funktionen $f_{1}\in C^{\infty }(G_{1})$ und $f_{2}\in C^{\infty }(G_{2})$ mittels der Vorschrift

$(f_{1}\otimes f_{2})(x,y)\mapsto f_{1}(x)f_{2}(y)$

ein Tensorprodukt definieren. Analog dazu kann man ein Tensorprodukt zwischen Distributionen definieren. Dazu werden zuerst reguläre Distributionen betrachtet. Seien $f_{1}\in L_{{loc}}^{1}(G_{1})$ und $f_{2}\in L_{{loc}}^{1}(G_{2})$ zwei lokal-integrierbare Funktionen, so folgt aus obiger Definition

${\begin{aligned}(f_{1}\otimes f_{2})(\phi )=&\int _{G_{1}\times G_{2}}f_{1}(x)f_{2}(y)\phi (x,y)\mathrm {d} (x,y)\\=&\int _{G_{1}}f_{1}(x)\int _{G_{2}}f_{2}(y)\phi (x,y)\mathrm {d} y\mathrm {d} x\\=&\int _{G_{2}}f_{2}(y)\int _{G_{1}}f_{1}(x)\phi (x,y)\mathrm {d} x\mathrm {d} y\end{aligned}}$

für alle $\phi \in C_{c}^{{\infty }}(G_{1}\times G_{2}).$ Daraus folgt

$(f_{1}\otimes f_{2})(\phi )=T_{{f_{1}}}(T_{{f_{2}}}(\phi ))=T_{{f_{2}}}(T_{{f_{1}}}(\phi )).$

Hieraus leitet man folgende Definition ab:

Definition

Seien $T_{1}\in {\mathcal {D}}'(G_{1})$ und $T_{2}\in {\mathcal {D}}'(G_{2})$ . Dann ist $T_{1}\otimes T_{2}$ eine Distribution aus ${\mathcal {D}}'(G_{1}\times G_{2})$ , die durch

${\begin{aligned}(T_{1}\otimes T_{2})(\phi )&:=T_{1}(T_{2}(\phi ))=T_{2}(T_{1}(\phi ))\\\end{aligned}}$

definiert ist.

Glättung einer Distribution

Distributionen können gezielt geglättet bzw. verschmiert bzw. approximiert werden, z.B., indem man die $\delta$ -Distribution durch die reguläre Distribution einer glatten Approximationsfunktionen ersetzt, wie z.B. die $\delta$ -Distribution durch die reguläre Distribution

$T_{\delta _{a}}(\varphi )=\int \limits _{\Omega }\delta _{a}(x)\varphi (x)\mathrm {d} x$

der oben definierte Funktion $\delta _{a}(x)$ oder die Heaviside-Distribution durch die reguläre Distribution der Integrale solcher Funktionen. Bei dreidimensionalen Differentialgleichungen kann man so z.B. feststellen, ob die Randbedingungen zu den Differentialgleichungen passen, die für das Innere gelten. Das ist für viele Anwendungen nützlich, zumal die Glättungsfunktionen, bis auf den Limes, nicht eindeutig vorgegeben sind, was zu erhöhter Flexibilität führt. Ebenso kann man auch gezielt Distributionen wie die obige PV-Distribution regularisieren, indem man z.B. die Testfunktionen mit geeigneten Faktoren versieht oder in anderer Weise vorgeht.

Faltung mit einer Funktion

Definition

Sei $T\in {\mathcal {D}}'(\mathbb{R} ^{n})$ eine Distribution und $\phi \in C_{c}^{\infty }(\mathbb{R} ^{n})$ eine Funktion, dann ist die Faltung von mit $\phi$ definiert durch

$(T*\phi )(x):=T(\phi (x-\cdot ))$ .

Beispiel

Sei $\mu$ ein Radon-Maß und sei $T_{\mu }\in {\mathcal {D}}'(\mathbb {R} ^{n})$ die mit dem Radon-Maß identifizierte Distribution. Dann gilt für die Faltung von $\mu$ mit $\phi \in C_{c}^{\infty }(\mathbb{R} ^{n})$

$(\mu *\phi )(x):=(T_{\mu }*\phi )(x)=T_{\mu }(\phi (x-\cdot ))=\int _{\mathbb {R} ^{n}}\phi (x-y)\mathrm {d} \mu (y).$

Eigenschaften

Falls eine glatte Funktion ist, so stimmt die Definition mit der Faltung von Funktionen überein.
Das Ergebnis der Faltung ist eine glatte Funktion, also gilt

$(T*\phi )\in C^{\infty }(\mathbb{R} ^{n})$ .
Für $T\in {\mathcal {D}}'(\mathbb{R} ^{n})$ und $\phi ,\psi \in C_{c}^{\infty }(\mathbb{R} ^{n})$ ist die Faltung assoziativ, das heißt, es gilt

$(T*\phi )*\psi =T*(\phi *\psi )\in C^{\infty }(\mathbb{R} ^{n})$ .
Für jeden Multiindex $\alpha$ gilt für die Ableitung der Faltung

$\partial ^{\alpha }(T*\phi )=(\partial ^{\alpha }T)*\phi =T*(\partial ^{\alpha }\phi )$ .

Faltung zweier Distributionen

Definition

Seien $T_{1}$ und $T_{2}$ zwei Distributionen, von denen mindestens eine kompakten Träger hat. Dann ist für alle $\phi \in C_{c}^{\infty }(\mathbb{R} ^{n})$ die Faltung zwischen diesen Distributionen definiert durch

$(T_{1}*T_{2})*\phi =T_{1}*(T_{2}*\phi )$ .

Die Abbildung

$C_{c}^{\infty }(\mathbb{R} ^{n})\ni \phi \mapsto T_{1}*(T_{2}*\phi )$

ist linear, stetig und kommutiert mit Verschiebungen. Daher gibt es eine eindeutige Distribution $T\in {\mathcal {D}}'(\mathbb{R} ^{n})$ , sodass

$T_{1}*(T_{2}*\phi )=T*\phi$

für alle $\phi \in C_{c}^{\infty }(\mathbb{R} ^{n})$ gilt.

Bemerkung: Die Bedingung, dass eine Distribution kompakten Träger hat, kann noch weiter abgeschwächt werden.

Eigenschaften

Diese Definition ist eine Verallgemeinerung der hier schon erwähnten Definitionen. Wählt man für $T_{i}$ eine reguläre Distribution, also eine Funktion, so entspricht dies den hier aufgeführten Definitionen. Es gelten die Eigenschaften:

Die Faltung ist kommutativ:

$T_{1}*T_{2}=T_{2}*T_{1}$
Für den Träger gilt:

$\operatorname {supp}(T_{1}*T_{2})\subseteq \operatorname {supp}(T_{1})+\operatorname {supp}(T_{2})$
Für den singulären Träger erhält man:

$\operatorname {sing}\,\operatorname {supp}(T_{1}*T_{2})\subseteq \operatorname {sing}\,\operatorname {supp}(T_{1})+\operatorname {sing}\,\operatorname {supp}(T_{2})$

Temperierte Distributionen

→ Hauptartikel: Temperierte Distribution

Die temperierten Distributionen bilden eine ausgezeichnete Teilmenge der bis hierhin betrachteten Distributionen auf dem Raum $\mathcal{D}(\R^n)$ . Auf den temperierten Distributionen ist es möglich, die Fourier- und die Laplace-Transformation zu erklären.

Fourier-Transformation

Um eine Fourier-Transformation ${\mathcal {F}}$ auf Distributionen definieren zu können, muss man die Menge der Distributionen erst einschränken. Nicht jede Funktion ist fouriertransformierbar, analog dazu kann man auch nicht für jede Distribution die Fouriertransformierte erklären. Aus diesem Grund entwickelte Laurent Schwartz den heute nach ihm benannten Schwartz-Raum $\mathcal{S}(\R^n)$ , indem er diesen Raum über eine Familie von Halbnormen definierte, die bezüglich der Multiplikation mit der Ortsvariablen und der Differentiation danach symmetrisch ist. Weil die Fouriertransformation Differentiation nach und Multiplikation mit vertauscht, impliziert diese Symmetrie, dass die Fouriertransformierte einer Schwartz-Funktion wieder eine Schwartz-Funktion ist. Auf diesem Raum ist daher die Fourier-Transformation ein Automorphismus, also eine stetige, lineare und bijektive Abbildung auf sich selbst. Der topologische Dualraum $\mathcal{S}'(\R^n)$ , also der Raum der stetigen, linearen Funktionale von ${\mathcal {S}}(\mathbb {R} ^{n})\to \mathbb {C}$ , heißt Raum der temperierten Distributionen. Die Menge der temperierten Distributionen $\mathcal S'$ ist umfangreicher als die Menge der Distributionen mit kompaktem Träger, ${\mathcal {E}}'$ , was daran liegt, dass die Menge der Schwartz-Funktionen eine Teilmenge des Raums der glatten Funktionen ist. Je kleiner ein Funktionenraum ist, desto größer ist nämlich sein Dualraum. Daher ist auch die Menge der temperierten Distributionen im Raum ${\mathcal {D}}'$ enthalten. Denn die Menge der glatten Funktionen mit kompaktem Träger ist eine Teilmenge des Schwartz-Raums.

Die Fouriertransformation von $T\in S'(\mathbb{R} ^{n})$ kann für alle $\phi \in S(\R^n)$ durch

${\mathcal {F}}(T)(\phi ):=T({\mathcal {F}}(\phi ))$

definiert werden. Auch auf $\mathcal{S}'(\R^n)$ ist die Fouriertransformation ein Automorphismus. Die Fouriertransformierte der Delta-Distribution ist eine konstante Distribution, ${\mathcal {F}}({\mathcal {\delta }})(\phi )=(2\pi )^{-n/2}(\phi )$ . Ein anderes Beispiel für eine temperierte Distribution ist der oben schon erwähnte Dirac-Kamm.

Faltungstheorem

Im Zusammenhang mit den obigen Definitionen der Faltung zweier Distributionen und der Fouriertransformation einer Distribution ist das Faltungstheorem interessant, das man wie folgt formulieren kann:

Sei $T_{1}\in {\mathcal {S}}'(\Omega )$ eine temperierte Distribution und $T_{2}\in {\mathcal {E}}'(\Omega )$ eine Distribution mit kompaktem Träger, dann gilt $T_{1}*T_{2}\in {\mathcal {S}}'(\Omega )$ und das Faltungstheorem für Distributionen besagt:

${\mathcal {F}}(T_{1}*T_{2})=(2\pi )^{{{\tfrac {n}{2}}}}{\mathcal {F}}(T_{1})\cdot {\mathcal {F}}(T_{2}).$

Die Multiplikation zweier Distributionen ist im Allgemeinen nicht definiert. In diesem besonderen Fall ist ${\mathcal {F}}(T_{1})\cdot {\mathcal {F}}(T_{2})$ allerdings sinnvoll, weil ${\mathcal {F}}(T_{2})$ eine glatte Funktion ist.

Differentialgleichungen

Da jede lokal-integrierbare $L_{{loc}}^{1}$ -Funktion, insbesondere auch jede $L^{2}$ -Funktion eine Distribution erzeugt, kann man diesen Funktionen im schwachen Sinn eine Distribution als Ableitung zuordnen. Lässt man Distributionen als Lösung einer Differentialgleichung zu, so vergrößert sich der Lösungsraum dieser Gleichung. Im Folgenden wird kurz dargelegt, was eine distributionelle Lösung einer Differentialgleichung ist und wie die Fundamentallösung definiert ist.

Lösungen im Distributionensinne

Sei

$P(x,\partial _{x})u=\sum _{{|\alpha |\leq m}}a_{\alpha }\partial _{x}^{\alpha }u$

ein Differentialoperator mit glatten Koeffizientenfunktionen $a_{\alpha }\in C^{\infty }(G)$ . Eine Distribution $u\in {\mathcal {D}}'(G)$ heißt Distributionenlösung von $P(x,\partial _{x})u(x)=f(x)$ , falls die von $P(x,\partial _{x})u$ und erzeugten Distributionen übereinstimmen. Dies bedeutet

$P(x,\partial _{x})u(\phi )=f(\phi )$

für alle $\phi \in {\mathcal {D}}(G)$ . Falls die Distribution regulär und sogar -mal stetig differenzierbar ist, dann ist eine klassische Lösung der Differentialgleichung.

Beispiel

Konstante Funktionen

Alle distributionellen Lösungen der eindimensionalen Differentialgleichung

${\frac {\partial }{\partial x}}u(x)=0$

sind die konstanten Funktionen. Das heißt, für alle $\phi \in {\mathcal {D}}(\mathbb{R} )$ wird die Gleichung

$\int _{\mathbb{R} }{\frac {\partial u}{\partial x}}(x)\phi (x){\mathrm {d}}x=\int _{\mathbb{R} }0\phi (x){\mathrm {d}}x\quad \Longleftrightarrow \quad \int _{\mathbb{R} }{\frac {\partial u}{\partial x}}(x)\phi (x){\mathrm {d}}x=0$

nur von konstantem gelöst.

Poisson-Gleichung

→ Hauptartikel: Poisson-Gleichung

Ein prominentes Beispiel ist die formale Identität

$\Delta \,{\frac {1}{|x-y|}}=-4\pi \,\delta (x-y)$

aus der Elektrostatik, wobei mit $\Delta$ der Laplace-Operator bezeichnet wird. Präzise bedeutet das

$\Delta \int _{{\mathbb{R} ^{3}}}{\frac {\phi (y)}{|x-y|}}{\mathrm {d}}^{3}y=-4\pi \phi (x).$

Das heißt

$U(x):=\int _{\mathbb {R} ^{3}}{\frac {\phi (y)}{|x-y|}}\mathrm {d} ^{3}y$

ist für alle $\phi \in {\mathcal {D}}(\mathbb{R} ^{3})$ eine Lösung der Poisson-Gleichung

$\Delta U(x)=-4\pi \phi (x).$

Man sagt auch, dass ${\tfrac {1}{|x-y|}}$ die hier betrachtete Poisson-Gleichung im distributionellen Sinn löst.

Fundamentallösungen

→ Hauptartikel: Fundamentallösung

Sei $P(x,\partial _{x})$ nun ein linearer Differentialoperator. Eine Distribution $H\in {\mathcal {D}}'(\mathbb{R} ^{n})$ heißt Fundamentallösung, falls die Differentialgleichung

$P(x,\partial _{x})u=\delta _{0}$

im Distributionensinne löst.

Die Menge aller Fundamentallösungen von $P(x,\partial _{x})$ ergibt sich durch Addition einer speziellen Fundamentallösung mit der allgemeinen homogenen Lösung $H_{0}$ . Die allgemeine homogene Lösung ist die Menge der Distributionen, für die $P(x,\partial _{x})u=0$ gilt. Nach einem Satz von Bernard Malgrange besitzt jeder lineare Differentialoperator mit konstanten Koeffizienten eine Fundamentallösung $H\in {\mathcal {D}}'(\mathbb{R} ^{n})$ .

Mit Hilfe dieser Fundamentallösungen erhält man durch Faltung Lösungen entsprechender inhomogener Differentialgleichungen. Sei eine glatte Funktion (oder allgemeiner eine Distribution mit kompaktem Träger), dann ergibt sich wegen

$P(x,\partial _{x})(H*f)=P(x,\partial _{x})H*f=\delta _{0}*f=f$

eine Lösung von $P(x,\partial _{x})u=f$ in der Form

wobei $H\in {\mathcal {D}}'(\mathbb{R} ^{n})$ genauso wie oben eine Fundamentallösung des Differentialoperators ist.

Harmonische Distributionen

Analog zu den harmonischen Funktionen definiert man auch harmonische Distributionen. So heißt eine Distribution harmonisch, wenn sie der Laplace-Gleichung

$\Delta T=0$

im distributionellen Sinne genügt. Da die distributionelle Ableitung allgemeiner ist als das gewöhnliche Differential, könnte man auch mehr Lösungen der Laplace-Gleichung erwarten. Das ist jedoch falsch. Denn man kann beweisen, dass es für jede harmonische Distribution $T\in {\mathcal {D}}'(\Omega )$ eine glatte Funktion gibt, die diese Distribution erzeugt. Es gibt also keine singulären Distributionen, die die Gleichung erfüllen, insbesondere ist der singuläre Träger einer harmonischen Distribution leer. Diese Aussage gilt sogar allgemeiner für elliptische partielle Differentialgleichungen. Für Physiker und Ingenieure bedeutet dies, dass sie in der Elektrodynamik, zum Beispiel in der Theorie der maxwellschen Gleichungen, unbedenklich mit Distributionen arbeiten können, auch wenn sie nur an gewöhnlichen Funktionen interessiert sind.

Distributionen als Integralkerne

→ Hauptartikel: Kernsatz von Schwartz

Jede Testfunktion $K\in {\mathcal {D}}(\Omega _{1}\times \Omega _{2})$ kann man durch

$({\mathcal {K}}\phi )(x)=\int _{{\Omega _{2}}}K(x,y)\phi (y){\mathrm {d}}y$

mit einem Integraloperator ${\mathcal {K}}\colon {\mathcal {D}}(\Omega _{2})\to C(\Omega _{1})$ identifizieren. Diese Identifikation kann auf Distributionen erweitert werden. So gibt es zu jeder Distribution $K\in {\mathcal {D}}'(\Omega _{1}\times \Omega _{2})$ einen linearen Operator

${\mathcal {K}}\colon {\mathcal {D}}(\Omega _{2})\to {\mathcal {D}}'(\Omega _{1}),$

der für alle $\psi \in {\mathcal {D}}(\Omega _{1})$ und $\phi \in {\mathcal {D}}(\Omega _{2})$ durch

$({\mathcal {K}}\phi )(\psi )=K(\phi \otimes \psi )$

gegeben ist. Außerdem gilt auch die Rückrichtung. So gibt es zu jedem Operator ${\mathcal {K}}$ eine eindeutige Distribution sodass $({\mathcal {K}}\phi )(\psi )=K(\phi ,\psi )$ gilt. Diese Identifikation zwischen Operator ${\mathcal {K}}\colon {\mathcal {D}}(\Omega _{2})\to {\mathcal {D}}'(\Omega _{1})$ und Distribution $K\in {\mathcal {D}}'(\Omega _{1}\times \Omega _{2})$ ist die Aussage des Kernsatzes von Schwartz. Die Distribution trägt auch den Namen Schwartz-Kern in Anlehnung an den Begriff des Integralkerns. Jedoch kann der Operator ${\mathcal {K}}\colon {\mathcal {D}}(\Omega _{2})\to {\mathcal {D}}'(\Omega _{1})$ nicht immer in Form eines Integralterms dargestellt werden.

Distributionen auf Mannigfaltigkeiten

Rücktransport

Man kann Distributionen mit Hilfe von Diffeomorphismen auf reellen Teilmengen hin- und zurücktransportieren. Seien $\Omega _{1},\,\Omega _{2}\subset \mathbb{R} ^{n}$ zwei reelle Teilmengen und $\psi \colon \Omega _{1}\to \Omega _{2}$ ein Diffeomorphismus, also eine stetig differenzierbare, bijektive Funktion, deren Umkehrabbildung ebenfalls stetig differenzierbar ist. Für $u\in C(\Omega _{2})$ gilt $u\circ \psi \in C(\Omega _{1})$ und für alle Testfunktionen $\phi \in {\mathcal {D}}(\Omega _{1})$ gilt aufgrund des Transformationssatzes die Gleichung

$\int _{\Omega _{1}}u(\psi (x_{1}))\phi (x_{1})\mathrm {d} x_{1}=\int _{\Omega _{2}}u(x_{2})\phi (\psi ^{-1}(x_{2}))\left|\det \left({\frac {\partial }{\partial x_{2}}}\psi ^{-1}(x_{2})\right)\right|\mathrm {d} x_{2}.$

Diese Identität motiviert folgende Definition für die Verkettung einer Distribution mit einem Diffeomorphismus: Sei $T\in {\mathcal {D}}'(\Omega _{2})$ , dann ist $T\circ \psi \in {\mathcal {D}}'(\Omega _{1})$ für alle $\phi \in {\mathcal {D}}'(\Omega _{2})$ definiert durch

$(T\circ \psi )(\phi )\colon =T\left(\left(\phi \circ \psi ^{{-1}}\right)\left|\det \left({\frac {\partial }{\partial x}}\psi ^{{-1}}\right)\right|\right).$

Meistens notiert man $T\circ \psi$ als $\psi ^{*}\,T$ und $\psi ^{*}$ heißt der Rücktransport der Distribution

Definition

Sei eine glatte Mannigfaltigkeit, $(\psi _{i}\colon \Omega _{i}\subset X\to {\tilde {\Omega }}_{i}\subset \mathbb{R} ^{n})_{{i\in I}}$ ein System von Karten und $T_{i}\in {\mathcal {D}}'({\tilde {\Omega }}_{i})$ , sodass für alle $\phi \in {\mathcal {D}}({\tilde {\Omega }}_{i}\cap {\tilde {\Omega }}_{j})$

$T_{{j}}(\phi )\colon =(\psi _{i}\circ \psi _{{j}}^{{-1}})^{*}\,T_{i}(\phi )$

in $\psi _{i}(\Omega _{j}\cap \Omega _{i})$ gilt. Dann nennt man das System $T\colon =(T_{i})_{{i\in I}}$ eine Distribution auf . Diese Distribution $T\in {\mathcal {D}}'(X)$ ist eindeutig bestimmt und von der Wahl der Karte unabhängig.

Es gibt noch andere Möglichkeiten, Distributionen auf Mannigfaltigkeiten zu definieren. Die Definition im Zusammenhang mit Dichtebündeln hat den Vorteil, dass dort kein System lokaler Karten gewählt werden muss.

Reguläre Distributionen auf Mannigfaltigkeiten

Bei dieser Definition kann man wieder jeder stetigen Funktion mittels der Integraldarstellung eine Distribution zuordnen. Sei also $u\in C(M)$ eine stetige Funktion auf der Mannigfaltigkeit, dann ist $u\circ \psi _{i}^{{-1}}$ eine stetige Funktion auf ${\tilde {\Omega }}_{i}\subset \mathbb {R} ^{n}$ . Mittels der Integraldarstellung für reguläre Distributionen

$T_{i}(\phi )\colon =\int _{{\tilde {\Omega }}_{i}}(u\circ \psi _{i}^{-1})(x_{i})\phi (x_{i})\mathrm {d} x_{i}$

erhält man ein System $(T_{i})_{{i\in I}},$ das eine Distribution auf bildet.

Literatur

Israel Gelfand: Verallgemeinerte Funktionen (Distributionen). VEB Deutscher Verlag der Wissenschaften, Berlin.
- Band 1: I. M. Gelfand, G. E. Schilow: Verallgemeinerte Funktionen und das Rechnen mit ihnen. 1960 (Hochschulbücher für Mathematik 47, ISSN 0073-2842).
- Band 2: I. M. Gelfand, G. E. Schilow: Lineare topologische Räume, Räume von Grundfunktionen und verallgemeinerten Funktionen. 1962 (Hochschulbücher für Mathematik 48).
- Band 3: I. M. Gelfand, G. E. Schilow: Einige Fragen zur Theorie der Differentialgleichungen. 1964 (Hochschulbücher für Mathematik 49).
- Band 4: I. M. Gelfand, N. J. Wilenkin: Einige Anwendungen der harmonischen Analyse. Gelfandsche Raumtripel. 1964 (Hochschulbücher für Mathematik 50).
- Nur in russischer Sprache: Обобщенные функции. Том 5: И. М. Гельфанд, М. И. Граев, Н. Я. Виленкин: Интегральная геометрия и связанные с ней вопросы теории представлений. Гос. Изд. Физ.-Мат. Лит., Москва 1962.
Lars Hörmander: The Analysis of Linear Partial Differential Operators. Band 1: Distribution Theory and Fourier Analysis. Second Edition. Springer-Verlag, Berlin u.a. 1990, ISBN 3-540-52345-6 (Grundlehren der mathematischen Wissenschaften 256).
Klaus-Heinrich Peters: Der Zusammenhang von Mathematik und Physik am Beispiel der Geschichte der Distributionen. Eine historische Untersuchung über die Grundlagen der Physik im Grenzbereich zu Mathematik, Philosophie und Kunst. Hamburg 2004 (Hamburg, Univ., Diss., 2004).

Basierend auf einem Artikel in:

Wikipedia.de