Projektive Geometrie
Die projektive Geometrie ist ein Teilgebiet der Geometrie. Sie ist aus der perspektivischen Darstellung dreidimensionaler Gegenstände in der zweidimensionalen Ebene hervorgegangen. Im Gegensatz zur „gewöhnlichen“ euklidischen Geometrie gibt es in der projektiven Geometrie keine Parallelen. Wesentliche Beiträge leisteten Jean Victor Poncelet 1822 und Karl Georg Christian von Staudt 1847.
Die projektive Geometrie befasst sich, wie die affine Geometrie, mit Punkten,
Geraden, Ebenen, Kurven und Flächen; allerdings ohne die Parallelität von
Geraden. Es gibt also keine Parallelprojektionen,
sondern nur Zentralprojektionen.
Die zu untersuchenden Objekte liegen jetzt in einer projektiven Ebene oder
einem projektiven
Raum. Meistens befasst man sich mit Objekten in einem projektiven Raum über
den reellen Zahlen
oder den komplexen Zahlen
,
das heißt, die Koordinaten der Punkte sind reelle bzw. komplexe Zahlen. Nur in
der axiomatischen projektiven Geometrie (s.u.) treten Koordinaten
aus allgemeineren Strukturen (Körper,
Schiefkörper, Ternärkörper, …)
auf. Projektive Ebenen/Räume, in denen der Satz
von Desargues gilt, lassen sich mit Hilfe von Vektorräumen über Schiefkörper
noch gut beschreiben. Dies zeigt die große Bedeutung des Satzes von Desargues.
Allerdings gilt er in mindestens 3-dimensionalen projektiven Räumen immer.
Der Einfachheit halber werden hier bis zum Abschnitt über axiomatische projektive Geometrie immer reelle Koordinaten vorausgesetzt.
Motivation
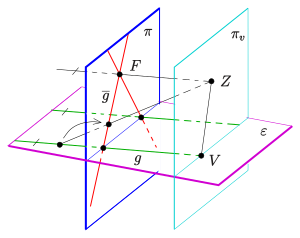
Eine Parallelprojektion
einer Ebene auf eine andere erhält die Parallelität der Geraden. Bei einer Zentralprojektion
(s. Bild) ist dies i.A. nicht mehr der Fall. Im Bild werden die zwei
grünen parallelen Geraden der horizontalen Ebene
durch die Zentralprojektion mit Zentrum
auf zwei sich im Punkt
schneidende (rote) Geraden der senkrechten Ebene
abgebildet. Der Punkt
besitzt allerdings kein Urbild. Man nennt ihn den Fluchtpunkt der grünen
Parallelenschar. Andererseits besitzt der Punkt
(in der zu
parallelen Ebene
)
der Gerade
kein Bild. Man nennt
den Verschwindungspunkt der Gerade
.
Eine Zentralprojektion ist also keine Bijektion (1-1-Abbildung) der Ebene
auf die Ebene
.
Der Ausweg aus diesem Dilemma: Man fügt in jeder Ebene jeder Parallelschar einen
weiteren Punkt hinzu, so dass sich parallele Geraden schneiden. Diese neuen
Punkte nennt man Fernpunkte und die Menge der Fernpunkte bildet die
Ferngerade der jeweiligen Ebene. Im Bild wird dann der Fernpunkt der
Gerade
auf den Fluchtpunkt
abgebildet. Der Verschwindungspunkt
wird auf den Fernpunkt der (roten) Gerade
abgebildet. Durch das Hinzufügen der Fernpunkte zu einer Ebene entsteht eine
neue Inzidenzstruktur mit den typischen Eigenschaften
- (1): je zwei Punkte haben genau eine Verbindungsgerade und
- (2): je zwei Geraden haben genau einen Schnittpunkt .
Man nennt diese neue Struktur die reelle projektive Ebene.
Diese
Art eine affine Ebene zu erweitern nennt man projektiv abschließen.
Dualitätprinzip
Vertauscht man in den Inzidenzeigenschaften (1), (2) (s.o.) die Begriffe Gerade und Punkt, sowie Schneiden und Verbinden, so werden lediglich die Aussagen (1) und (2) vertauscht. Hat man also eine Aussage, die nur die Begriffe Gerade, Punkt, schneiden und verbinden verwendet, so gilt auch ihre duale Aussage. Zum Beispiel erhält man durch Dualisierung des Satzes von Pascal den Satz von Brianchon. Der Satz von Desargues ist gleich seiner dualen Aussage. Aber der duale Satz von Pappus ist eine weitere Aussage über projektive Ebenen.
Für affine Ebenen gilt das Dualitätsprinzip nicht.
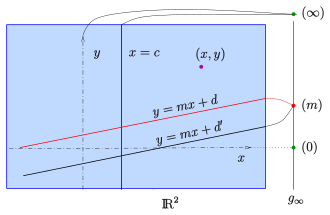
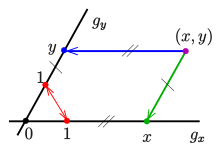
Inhomogene Koordinaten
Um einem Punkt einer reellen projektiven Ebene Koordinaten zuzuordnen,
beschreibt man einen endlichen Punkt (keinen Fernpunkt) in gewohnter
Weise durch .
Für den Fernpunkt der Gerade
bietet sich die Steigung
(einschließlich
)
an (s. Bild). Da ein Punkt entweder durch zwei Koordinaten oder durch eine
Koordinate (Fernpunkt) beschrieben wird, nennt man diese Koordinaten
inhomogene Koordinaten. Gegenüber den homogenen Koordinaten, haben
inhomogene Koordinaten den großen Vorteil: Sie sind eindeutig und man kann im
endlichen Bereich in gewohnter Weise rechnen.
Homogene Koordinaten
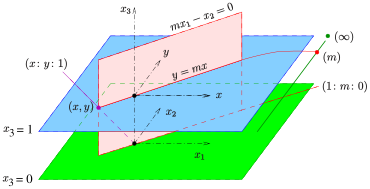
Dass die reelle projektive Ebene in ihrer inhomogenen Beschreibung nur formal
eine inhomogene Struktur ist, zeigt ihre Beschreibung mit homogenen
Koordinaten. Hierzu definiert man im
- jede Ursprungsgerade ist ein (projektiver) Punkt und
- jede Ursprungsebene ist eine (projektive) Gerade.
Ein Punkt inzidiert mit einer Gerade, wenn die dem Punkt entsprechende
Ursprungsgerade in der der Geraden entsprechenden Ursprungsebene liegt. Man kann
zeigen, dass die so definierte Inzidenzstruktur geometrisch zu dem oben
definierten Modell der reellen projektiven Ebene äquivalent, isomorph,
ist. Das Bild zeigt die Einbettung der endlichen Punkte des inhomogenen Modells
der reellen projektiven Ebene in den
als Ebene mit der Gleichung
.
Die Rolle der Ferngerade übernimmt die Ebene
.
Jede Ursprungsgerade dieser Ebene ist ein Fernpunkt. Das Bild zeigt die
Zuordnung der Fernpunkte beider Modelle. Da ein vom Nullpunkt verschiedener
Punkt
eine Ursprungsgerade und damit einen Punkt der projektiven Ebene beschreibt,
nennt man
seine homogenen Koordinaten und
- bezeichnet den (projektiven) Punkt mit
.
Da eine Ursprungsgerade aber durch jeden beliebigen vom Nullpunkt verschiedenen Punkt auf ihr beschrieben werden kann, gilt
.
D.h., homogene Koordinaten beschreiben die Punkte der reellen projektiven
Ebene nicht eindeutig. Dies ist ein Nachteil gegenüber inhomogenen
Koordinaten. Eine Gerade (Ursprungsebene) wird im homogenen Modell durch
eine Gleichung
beschrieben.
Die Koordinaten endlicher Punkte (keine Fernpunkte) lassen sich umrechnen durch
bzw.
Der große Vorteil der homogenen Koordinaten ist
- Jede inzidenzerhaltende Abbildung (Kollineation) wird durch eine lineare Abbildung (Matrix) beschrieben.
(Eine affine Abbildung ist eine Kombination aus einer linearen Abbildung und einer Verschiebung.)
Bettet man die x-y-Ebene so ein, dass sie im
gleich der Ebene
ist, so wird die Ursprungsebene
zur Ferngerade. In diesem Fall sind die homogenen Koordinaten die
baryzentrischen
Koordinaten bezüglich des Dreiecks
.
n-dimensionaler projektiver Raum
Die Beschreibung der reellen projektiven Ebene mit homogenen Koordinaten
zeigt, dass man einen n-dimensionalen projektiven
Raum analog im
definieren kann:
- Die Punkte sind die Ursprungsgeraden des
- Die Geraden sind die Ursprungsebenen.
Für
erhält man die projektive
Gerade. Sie ist als Inzidenzstruktur zwar uninteressant, aber die auch
hier definierte Gruppe der projektiven Permutationen ist als projektive
lineare Gruppe
interessant. Sie operiert im homogenen Modell auf den Ursprungsgeraden
des
als Matrizengruppe oder im inhomogenen Modell als gebrochen lineare
Abbildungen
.
Eine wesentliche Eigenschaft ist:
- Die Gruppe
operiert scharf 3-fach-transitiv, d.h. zu je zwei Punktetripeln gibt es genau eine Abbildung, die das eine auf das andere abbildet.
Kollineation, Zentralkollineation, Projektivität
- Kollineation
- Eine Kollineation
einer projektiven Ebene ist eine bijektive Abbildung
der Punktmenge
auf sich, die kollineare Punkte auf kollineare Punkte abbildet.
permutiert sowohl die Menge der Punkte
als auch die Menge
der Geraden.
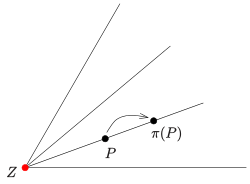
- Zentralkollineation
Wichtige Kollineationen einer projektiven Ebene sind die Zentralkollineationen (auch Perspektivitäten genannt).
- Eine Zentralkollineation lässt einen Punkt, das Zentrum, und alle Geraden durch diesen Punkt fest.
Man kann nachweisen, dass es dann eine Gerade, die Achse, gibt, deren Punkte alle fix bleiben. Es kann allerdings vorkommen, dass das Zentrum auch auf der Achse liegt. In diesem Fall nennt man die Zentralkollineation Elation, andernfalls Homologie. Ist die Achse die Ferngerade, so ist eine Zentralprojektion im endlichen (affinen) Teil eine Punktstreckung oder eine Translation (Verschiebung).
- Projektivität
- Eine Hintereinanderausführung von mehreren Zentralkollineationen nennt man projektive Kollineation oder Projektivität.
Für die reelle projektive Ebene gilt
- (PR): Jede Kollineation ist eine projektive Kollineation und kann in homogenen Koordinaten durch eine lineare Abbildung beschrieben werden.
- Beispiel
Die Translation
wird in homogenen Koordinaten (s.o.) durch
und damit als lineare Abbildung mit der Matrix
beschrieben.
Mehr Beispiele findet man in dem Artikel Homogene Koordinaten.
Die von den 3×3-Matrizen erzeugte projektive Kollineationsgruppe der reellen
projektiven Ebene ist die projektive
lineare Gruppe
Die Eigenschaft (PK) ist nicht allgemeingültig. So gibt es zum Beispiel in
der komplexen projektiven Ebene Kollineationen, die nur als semilineare
Abbildungen dargestellt werden können. Z.B.:
- Kollineation zwischen Inzidenzstrukturen
Eine projektive Ebene/Raum kann meistens mit wenigstens zwei Modellen
(inhomogen, homogen) beschrieben werden. Um nachzuweisen, dass zwei
Inzidenzstrukturen
dieselbe Geometrie beschreiben, ist es nötig, eine bijektive Abbildung von
auf
anzugeben, die kollineare Punkte auf kollineare Punkte abbildet. D.h. man muss
den Begriff Kollineation entsprechend erweitern. Im Allgemeinen ist
- eine Kollineation eine Abbildung von einer Inzidenzstruktur auf eine zweite, die Geraden auf Geraden abbildet.
Dualität, Polarität
- Eine bijektive Abbildung der Punkte
einer projektiven Ebene
auf die Menge der Geraden
, die kollineare Punkte auf kopunktale Geraden abbildet und umgekehrt, heißt Dualität oder in älterer Literatur Korrelation.
Eine Dualität ist also eine Kollineation einer projektiven Ebene auf ihre duale projektive Ebene.
Beispiel: Die Abbildung der reellen projektiven Ebene, die einem Punkt
(in homogenen Koordinaten) die Ebene mit der Gleichung
zuordnet und umgekehrt, ist eine Dualität.
Besondere Dualitäten sind Polaritäten:
- Eine Dualität
heißt Polarität, wenn aus der Inzidenz von
mit der Gerade
folgt, dass
auf
liegt.
heißt Polare von
und
Pol von
.
- Eine Polarität ist immer involutorisch, d.h.
Identität.
Die Dualität im obigen Beispiel ist eine Polarität.
- Gibt es bei einer Polarität Punkte, die auf ihrer Polaren liegen, so nennt man die Polarität hyperbolisch (z. B. Pol-Polare-Beziehung zu einem nicht ausgearteten Kegelschnitt), im anderen Fall elliptisch.
Das obige Beispiel einer Polarität ist elliptisch. Wesentlich hierfür ist
allerdings, dass die zugrunde liegende projektive Ebene die reelle Ebene
ist ! Sind die Koordinaten komplexe Zahlen, ist die Polarität
hyperbolisch, denn in diesem Fall hat die Gleichung
nichttriviale Lösungen: z.B. liegt der Punkt
auf seiner Polaren
.
Doppelverhältnis
Bei projektiven Abbildungen in einem projektiven Raum ist das Teilverhältnis nicht mehr invariant (z.B.: Der Mittelpunkt einer Strecke geht nicht mehr in den Mittelpunkt der Bildstrecke über). Das Analogon zum Teilverhältnis ist in der projektiven Geometrie das Doppelverhältnis (Verhältnis zweier Teilverhältnisse).
Im
ist das Teilverhältnis
,
in dem ein Punkt
eine Strecke
teilt, die durch die Beziehung
definierte Zahl
.
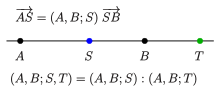
- Beispiele
1) Ist ,
so ist
der Mittelpunkt der Strecke
.
2) Für
teilt
die Strecke im Verhältnis
3) Für
liegt
außerhalb und
teilt die Strecke
im Verhältnis
.
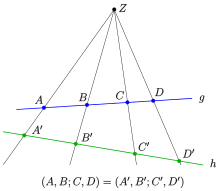
Im
ist das Doppelverhältnis
,
in dem ein Punktepaar
eine Strecke
teilt, die Zahl
(Verhältnis zweier Teilverhältnisse).
Das Doppelverhältnis, das hier zunächst nur für die affinen Punkte der reellen projektiven Ebene/Raum definiert wurde, lässt sich in homogenen Koordinaten mit Hilfe von Verhältnissen von Determinanten einheitlich ausdrücken (s. Doppelverhältnis).
Die große Bedeutung des Doppelverhältnisses beruht auf der Eigenschaft
- Das Doppelverhältnis ist bei Projektivitäten invariant.
Ist das Doppelverhältnis zweier Punktepaare ,
so spricht man von einer harmonischen
Teilung. Liegen die Punkte
harmonisch und ist
der Fernpunkt der Gerade, so ist
der Mittelpunkt der Strecke
.
Affine Beschränkung (schlitzen)
Aus einem projektiven Raum lassen sich immer durch Herausnehmen von Hyperebenen (schlitzen) wieder affine Räume herstellen. Damit lassen sich die in einem projektiven Raum gewonnenen Resultate durch eine geeignete Wahl einer Ferngerade/-Hyperebene dann auch affin beschreiben. So sind z.B. einige Eigenschaften von Parabel und Hyperbel einfach die affinen Versionen von Ausartungen des Satzes von Pascal für einen projektiven Kegelschnitt.
Projektiver Kegelschnitt, Quadriken
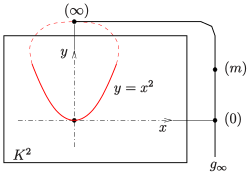
Projektiver Kegelschnitt
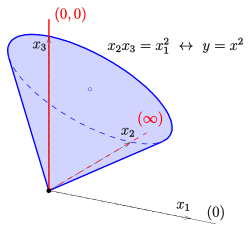
Stellt man die Parabel
gemäß obiger Umrechnung (
)
in homogenen Koordinaten dar, so erhält man die Gleichung
.
Diese Gleichung beschreibt im
einen Kegel mit der Spitze im Ursprung. Er berührt die Ebene
in der
-Achse.
Diese Gleichung ist also auch für den Fernpunkt
(der y-Achse) erfüllt. Das Nullstellengebilde der homogenen Gleichung besteht
aus den Parabelpunkten plus einem Fernpunkt.
- Man nennt die projektive Kurve mit der Gleichung
und alle dazu projektiven Bilder einen nicht ausgearteten projektiven Kegelschnitt.
(Ein n.a. projektiver Kegelschnitt lässt sich auch über andere Eigenschaften definieren. Z.B.: Steiner-Erzeugung, v.Staudt-Kegelschnitt oder durch Symmetrien. Siehe hierzu die Artikel über projektive Kegelschnitte und über Ovale.)
Stellt man die Hyperbel
in homogenen Koordinaten dar, so erhält man die Gleichung
.
Diese Gleichung ist auch für die beiden Fernpunkte
(der x- bzw. y-Achse) erfüllt. Man erkennt, dass diese Gleichung durch den
Koordinatenwechsel
(lineare Abbildung) in die aus der Parabel entstandene Kurve übergeht. Sie ist
damit auch ein projektiver Kegelschnitt.
Geht man vom Einheitskreis
aus, erhält man zunächst
und daraus
.
Auch diese Gleichung lässt sich durch eine lineare Abbildung in die erste
Gleichung transformieren.
Ein Kegelschnitt besitzt besonders viele Automorphismen (Kollineationen, die den Kegelschnitt invariant lassen).
- Die Automorphismengruppe eines projektiven Kegelschnitts ist
isomorph zur Gruppe
. (Diese ist 3-fach-transitiv, d.h. zu je zwei Tripeln von Punkten gibt es eine Kollineation, die das eine Tripel auf das andere abbildet.)
Projektive Quadriken
Analog zu einem projektiven Kegelschnitt lassen sich projektive Quadriken in projektiven Räumen in homogenen Koordinaten als Nullstellengebilde von quadratischen Formen beschreiben.
Wie bei Kegelschnitten fallen im 3-dimensionalen projektiven Raum affin verschiedene Quadriken zusammen. Z.B.: Kegel und Zylinder oder Ellipsoid und elliptisches Paraboloid.
Plücker-Koordinaten und Klein-Quadrik
Im 3-dimensionalen reellen projektiven Raum
lässt sich
ein Punkt (1-dim. Unterraum des )
in homogenen Koordinaten durch
und
eine Ebene (3-dim. Unterraum) mit der Gleichung
durch den (projektiven) Punkt
beschreiben.
Für die bei vielen Untersuchungen wichtigen Geraden (Ursprungsebenen) gibt es keine so einfache homogene Beschreibung. Überlegungen von J. Plücker führten zur Einführung der nach ihm benannten Plücker-Koordinaten :
Eine Gerade
ist durch ein Paar von Punkten
auf ihr eindeutig bestimmt. Plücker konnte zeigen, dass die sechs 2x2-Determinanten
bis auf ein gemeinsames Vielfaches die Gerade durch
eindeutig bestimmen. Die Gerade
lässt sich also durch den Punkt
des 5-dimensionalen reellen projektiven Raums
beschreiben.
Die durch die Geraden des
bestimmten Punkte überdecken allerdings nicht den ganzen
.
Denn die Determinanten müssen noch die homogene quadratische Gleichung, die
Plücker-Relation, erfüllen:
.
Diese Gleichung beschreibt eine projektive
Quadrik im 5-dimensionalen projektiven Raum, die als Klein-Quadrik
bezeichnet wird. Jeder Punkt der Klein-Quadrik repräsentiert eine Gerade des
.
Das Konzept der Plücker-Koordinaten lässt sich auf jeden 3-dimensionalen pappusschen projektiven Raum (der Koordinatenbereich ist ein Körper) übertragen.
Homogene Darstellung rationaler Kurven
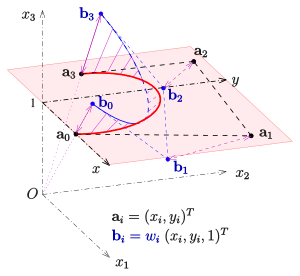
Eine Kurve mit einer rationalen Darstellung
wobei die Funktionen
und
Polynome sind, lässt sich in homogenen Koordinaten polynomial darstellen:
Eine ebene Kurve mit rationalen Koeffizientenfunktionen lässt sich also als
Zentralprojektion einer polynomialen Kurve des
auf die Einbettungsebene
auffassen.
Auf diese Weise lässt sich z.B. eine rationale Bezierkurve mit Hilfe einer Projektion einer gewöhnlichen (polynomialen) Bezier-Kurve darstellen. Insbesondere Ellipsen- und Hyperbelbögen sind Projektionen von Bezierkurven vom Grad 2 (Parabeln).
Axiomatische projektive Geometrie
In der axiomatischen projektiven Geometrie geht man zunächst von sehr schwachen Axiomen, den Inzidenzaxiomen aus. Eine so definierte projektive Ebene besteht aus einer Menge von Punkten und einer Menge von Geraden mit den einfachen Inzidenzeigenschaften
- (1:) Je zwei Punkte haben genau eine Verbindungsgerade und
- (2:) Je zwei Geraden haben genau einen Schnittpunkt.
Solch eine projektive Ebene ist noch sehr weit von der reellen projektiven Ebene entfernt. Erst durch ein zusätzliches Axiom (Satz von Pappos) ist solch eine projektive Ebene überhaupt erst mit Hilfe eines Vektorraums über einem Körper beschreibbar und damit lineare Algebra einsetzbar. Um zu erreichen, dass dieser Körper sogar die reellen Zahlen sind, sind noch einige weitere Axiome nötig. (Siehe Hilberts Axiomensystem der euklidischen Geometrie)
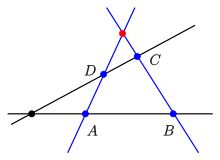
Da in einem projektiven Raum sich Geraden nicht unbedingt schneiden müssen, aber andererseits jede ebene Punktmenge eine projektive Ebene sein soll, muss man im Raum Axiom (2) durch das Veblen-Young-Axiom ersetzen:
- (Axiom
von Veblen-Young) Sind
,
,
,
vier Punkte, so dass
und
mit einem gemeinsamen Punkt inzidieren, so inzidieren auch
und
mit einem gemeinsamen Punkt.
In einem mindestens 3-dimensionalen projektiven Raum gilt, im Gegensatz zum ebenen Fall, immer der Satz von Desargues und der Raum ist dann über einem Schiefkörper (nicht notwendig kommutativer Körper) koordinatisierbar.
Im ebenen Fall gibt es zahlreiche sog. nicht desarguessche projektive Ebenen, die in der Regel durch einen Schließungssatz, z.B. dem kleinen Satz von Desargues (Zentrum liegt auf der Achse) oder durch die Reichhaltigkeit der Automorphismengruppe (Gruppe der Kollineationen auf sich) charakterisiert werden. Eine Klasseneinteilung der nichtdesargueschen Ebenen liefert die Lenz-Barlotti-Klassifikation.
Die Sätze von Desargues und Pappus
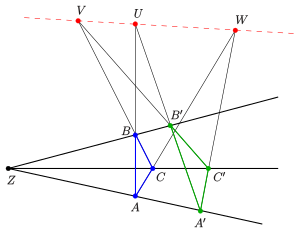
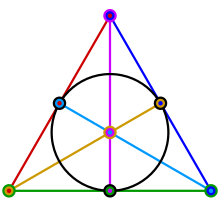
- Satz von Desargues
- Liegen zwei Dreiecke
und
perspektiv mit Zentrum
, so sind die Schnittpunkte
der Geraden durch sich entsprechende Seiten kollinear (s. oben, erstes Bild).
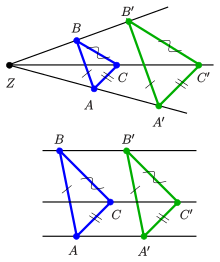
Die große Bedeutung dieses Satzes besteht in der Möglichkeit, eine projektive Ebene, in der für alle möglichen Konfigurationen der Satz gilt, einen Schiefkörper für eine inhomogene Koordinatisierung zu konstruieren. Dabei beschränkt man die projektive Ebene durch Herausnahme (Schlitzen) einer Gerade auf eine affine Ebene, in der dann die affine Formen des Satzes von Desargues gelten:
- (GD): (großer Desargues) Liegen zwei Dreiecke
und
perspektiv mit Zentrum
, so folgt aus der Parallelität zweier Seitenpaare die Parallelität des dritten Seitenpaares (s. Bild).
- (KD): (kleiner Desargues) Liegen zwei Dreiecke
und
auf drei parallelen Geraden, so folgt aus der Parallelität zweier Seitenpaare die Parallelität des dritten Seitenpaares (s. Bild).
In der nun affinen Ebene wählt man zwei sich in einem Punkt
schneidende Geraden
.
(
wird zum Ursprung des Koordinatensystems und
werden zur x- und y-Achse.) Mit Hilfe des kleinen Satzes von Desargues definiert
man zunächst Translationen und damit dann auf den Punkten der Gerade
eine Addition. Mit Hilfe des großen Satzes konstruiert man
Punktstreckungen und damit eine Multiplikation.
Schließlich lässt sich zeigen, dass Addition und Multiplikation aus der
Punktmenge von
einen Schiefkörper machen. Mit Hilfe einer Parallelprojektion (im Bild rot)
lässt sich dieser Koordinatenschiefkörper auch auf die Gerade
übertragen. Damit lässt sich dann jedem Punkt
der affinen Ebene in gewohnter Weise ein Koordinatenpaar
zuordnen. Eine Gerade wird (wie üblich) durch eine Gleichung
oder
beschrieben. Die so koordinatisierte affine Ebene lässt sich dann wieder durch
Hinzunahme von Fernpunkten (s.o.) zu einer inhomogenen Beschreibung der
projektiven Ebene erweitern. Auch die homogene Darstellung (s.o.) ist
möglich. Da der Koordinatenschiefkörper allerdings nicht notwendig kommutativ
ist, muss man auf die Reihenfolge bei der Multiplikation achten.

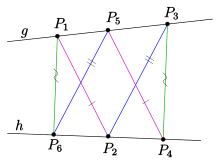
Liegen sechs Punkte
einer projektiven Ebene abwechselnd auf zwei Geraden
und
,
so sind die Punkte
kollinear, d.h., sie liegen auf einer Gerade
(siehe Bild).
Ist die Gerade
die Ferngerade, so erhält man die affine Form des Satzes.
Die Bedeutung dieses Satzes besteht darin, dass seine Gültigkeit in einer desarguesschen Ebene aus dem Koordinatenschiefkörper einen Körper (Multiplikation ist kommutativ) macht. Aber die Bedeutung des Satzes von Pappus ist noch viel größer, denn es gilt
- (Satz von Hessenberg) In einer projektiven Ebene, in der der Satz von Pappus gilt, gilt auch der Satz von Desargues.
Das heißt: Aus der alleinigen Gültigkeit des Satzes von Pappus lässt sich schon ein Körper konstruieren. Allerdings ist eine endliche desarguessche Ebene immer schon pappussch, da jeder endliche Schiefkörper kommutativ ist (Satz von Wedderburn).
Projektive Abbildungen von Punktreihen und Geradenbüschel
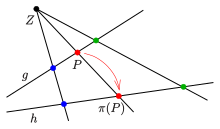
Sind
zwei Geraden einer projektiven Ebene und
ein Punkt, der nicht auf beiden Geraden liegt, so nennt man die Abbildung, die
einen Punkt
der Gerade
auf den Schnittpunkt
abbildet (projiziert) eine perspektive Abbildung (auch perspektive
Zuordnung genannt) von
auf
mit Zentrum
.
Eine Hintereinanderausführung mehrerer solcher Abbildungen nennt man eine projektive Abbildung. (Man beachte, dass hier nicht von einer Kollineation der projektiven Ebene die Rede ist. Es werden dabei lediglich die Punkte der Ausgangsgerade auf die Punkte der Zielgerade abgebildet.)
Ist die Zielgerade gleich der Ausgangsgerade
(nur bei echt projektiven Abbildungen), so gilt für die Menge
aller projektiven Abbildungen von
auf sich
- (1)
ist eine Gruppe,
- (2)
operiert auf der Punktmenge von
3-fach-transitiv, d.h. zu je zwei Tripeln von Punkten gibt es eine projektive Abbildung, die das eine Tripel auf das andere abbildet.
Die Bedeutung der projektiven Abbildungen zeigt der Satz
- (3) Eine projektive Ebene ist genau dann pappussch, wenn
eine projektive Abbildung einer Geraden
auf sich, die 3 Fixpunkte besitzt, nur die Identität sein kann. Daraus folgt, dass
sogar scharf transitiv ist.
Weiterhin gilt:
- (4) In einer pappusschen projektiven Ebene über einem Körper
ist
isomorph zu
.
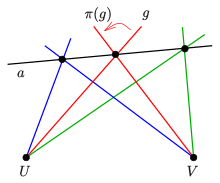
Aufgrund des Dualitätsprinzips gibt es auch perspektive/projektive Abbildungen von einem Geradenbüschel auf ein anderes:
Sind
zwei Punkte einer projektiven Ebene und
eine Gerade, die nicht durch die beiden Punkte geht, so nennt man die Abbildung,
die eine Gerade
des Geradenbüschels in
auf die Gerade
abbildet (projiziert) eine perspektive Abbildung des Geradenbüschels in
auf das Geradenbüschel in
mit Achse
.
Eine Hintereinanderausführung mehrerer solcher Abbildungen nennt man eine
projektive Abbildung des einen Büschels auf das andere.
Die Aussagen (1) – (4) gelten in analoger Weise auch für projektive Abbildungen von Geradenbüscheln.
Eine projektive Abbildung eines Geradenbüschels auf ein anderes spielt bei Steiners Definition eines projektiven Kegelschnitts (s. Satz von Steiner) eine wesentliche Rolle.
Endliche projektive Ebenen/Räume
Setzt man voraus, dass die Punktmenge (und damit auch die Geradenmenge) endlich ist, erhält man eine endliche projektive Ebene/Raum. Einfache Beispiele sind die projektiven Ebenen über endlichen Körpern. Da es keine echten endlichen Schiefkörper gibt (Satz von Wedderburn), ist jede endliche desarguessche Ebene bzw. Raum schon pappussch also über einem Körper koordinatisierbar.
Für eine endliche projektive Ebene gilt:
- Enthält eine Gerade
Punkte, so enthalten alle Geraden
Punkte, durch jeden Punkt gehen
Geraden und insgesamt gibt es
Geraden und
Punkte.
heißt in diesem Fall die Ordnung der endlichen Ebene.
Endliche projektive Ebenen spielen auch in der kombinatorischen Geometrie als Beispiele von Blockplänen eine Rolle.
Fano-Axiom
Es gibt (axiomatische) affine Ebenen, in denen sich die Diagonalen in einem Parallelogramm nicht schneiden, was unserer Erfahrung aus der reellen Ebene widerspricht. Um dies zu verhindern, schließt man solche Fälle mit dem affinen Fano-Axiom aus. Bei projektiven Ebenen leistet dies das projektive Fano-Axiom. Es lautet:
- (F): Die Schnittpunkte der Gegenseiten (Diagonalpunkte) in einem beliebigen vollständigen Viereck sind nicht kollinear.
Beschränkt man eine projektive Ebene, die dem Fano-Axiom genügt, so entsteht eine affine Ebene, in der die Diagonalen eines Parallelogramms nie parallel sind. Das Minimalmodell ist keine Fano-Ebene. Nimmt man aus dem Minimalmodell eine Gerade heraus, so entstehen Parallelogramme, deren Diagonalen parallel sind.
Pappussche Fano-Ebenen sind solche, die über einem Körper der Charakteristik
,
d.h.
,
beschrieben werden können.
Ovale, Ovoide, quadratische Mengen
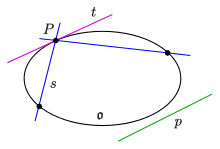
Neben Geraden und Ebenen spielen in projektiven Ebenen Ovale und in projektiven Räumen Ovoide als die nächst einfachen Kurven und Flächen eine Rolle.
- Ein Oval in einer projektiven Ebene ist eine Punktmenge, die von einer Gerade in höchstens zwei Punkten geschnitten wird und in jedem Punkt gibt es genau eine Tangente (Gerade mit einem Schnittpunkt).
Einfache Beispiele von Ovalen sind die n.a. projektiven Kegelschnitte. Während n.a. projektiven Kegelschnitte nur in pappusschen Ebenen existieren, gibt es Ovale fast in jeder projektiven Ebene. Die Kegelschnitte zeichnen sich durch Schließungssätze (Pascal, Brianchon) und durch besonders viele Symmetrien aus (s.o.).
In der reellen projektiven Ebene erhält man durch Zusammensetzen eines
Halbkreises und einer geeigneten Halbellipse Ovale, die keine Kegelschnitte
sind. Die Kurve mit der Gleichung
ist auch ein Oval, das kein Kegelschnitt ist.
Für endliche projektive Ebenen (d.h. die Punktmenge und Geradenmenge sind endlich) gilt
- In einer projektiven Ebene der Ordnung
(d.h. jede Gerade enthält
Punkte) ist eine Menge
genau dann ein Oval, wenn
ist und keine drei Punkte von
kollinear (auf einer Gerade) liegen.
Ist die Ebene pappussch und ungerader Ordnung gilt sogar:
- (Satz von Segre) In einer endlichen pappusschen Ebene ungerader Ordnung ist jedes Oval ein projektiver Kegelschnitt.
In einer pappusschen Ebene gerader Ordnung ist dieser Satz in seiner Allgemeinheit falsch. Es gibt Ovale, die keine Kegelschnitte sind.
Das räumliche Analogon zu einem Oval ist das Ovoid:
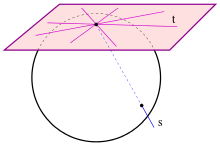
- Ein Ovoid in einem projektiven Raum ist eine Menge von Punkten, die von einer Gerade in höchstens zwei Punkten geschnitten wird und die Menge der Tangenten durch einen Punkt überdecken genau eine Hyperebene.
Einfache Beispiele von Ovoiden im reellen projektiven Raum sind Ellipsoide. Setzt man eine Halbkugel und ein Halbellipsoid passend zusammen erhält man ein Beispiel, das keine Quadrik ist.
Für endliche projektive Räume der Dimension
ist der Raum über einem Körper koordinatisierbar
und es gilt:
- Ist
ein Ovoid in einem endlichen projektiven Raum der Dimension
, so ist
(Es gibt also im endlichen Fall nur im 3-dimensionalen Raum Ovoide !)
- In einem projektiven Raum der Ordnung
und Dimension
ist eine Menge von Punkten
genau dann ein Ovoid, wenn
ist und keine drei Punkte von
kollinear (auf einer Gerade) liegen.
Eine Folge des Satzes von Segre ist:
- Im 3-dimensionalen Raum ungerader Ordnung ist jedes Ovoid schon eine Quadrik.
Wie im ebenen Fall ist dieser Satz für Räume gerader Ordnung falsch. Im geraden Fall gibt es Ovoide (Tits-Suzuki-Ovoide), die keine Quadriken sind.
Quadratische Mengen sind noch allgemeiner. Sie besitzen dasselbe Schnittverhalten mit Geraden wie Quadriken, müssen aber keine sein. Einfache Beispiele hierzu sind der Kegel und das einschalige Hyperboloid. Aber es gibt auch quadratische Mengen, die keine Quadriken sind.
Topologische projektive Ebenen
Eine topologische projektive Ebene ist eine projektive Ebene, auf deren Punkt- und Geradenmenge je eine Topologie so erklärt ist, dass die Bildung des Schnittpunktes von zwei Geraden und die Bildung der Verbindungsgeraden stetige Operationen sind.
Projektive algebraische Geometrie
Statt im affinen Raum
zu arbeiten, geht man in der algebraischen
Geometrie oft zum projektiven
Raum über. Der Hauptvorteil besteht dabei darin, dass sich die Anzahl der
Schnittpunkte zweier Varietäten dann leicht mit Hilfe des Satzes von Bézout
bestimmen lässt.
Projektiver Raum als Verband
Ein projektiver Raum und seine Unterräume lässt sich auch als ein spezieller Verband auffassen:
- Der Verband der Unterräume eines endlich dimensionalen projektiven Raums ist äquivalent zu einem endlich dimensionalen komplementierten atomaren modularen Verband.
Literatur
- F. Bachmann: Aufbau der Geometrie aus dem Spiegelungsbegriff, 1959, (2. Auflage. Springer 1973)
- W. Blaschke: Projektive Geometrie, Springer-Verlag, 2013, ISBN 3-0348-6932-0
- Albrecht Beutelspacher: Einführung in die endliche Geometrie. I. Blockpläne. B.I. Wissenschaftsverlag, Mannheim/Wien/Zürich 1982, ISBN 3-411-01632-9.
- A. Beutelspacher, U. Rosenbaum: Projektive Geometrie Vieweg + Teubner, Braunschweig u. a. 1992, ISBN 3-528-07241-5
- H. Brauner: Geometrie projektiver Räume I,II, BI-Verlag, 1976
- David Hilbert: Grundlagen der Geometrie. 14. Auflage. Teubner, Stuttgart 1999, ISBN 3-519-00237-X.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 15.01. 2022