Norton-Theorem

Das Norton-Theorem (nach Edward Lawry Norton; auch: Mayer-Norton-Theorem) besagt in der Theorie linearer elektrischer Netzwerke, dass jede mögliche Kombination von linearen Spannungsquellen, Stromquellen und Widerständen bezüglich zweier Klemmen elektrisch äquivalent zu einer Parallelschaltung aus einer Stromquelle und einem ohmschen Widerstand ist. Äquivalenz bedeutet, dass sich bei gleicher äußerer Belastung gleiches Verhalten von Spannung und Stromstärke einstellt.

Diese Ersatzschaltung wird Norton-Äquivalent oder Ersatzstromquelle genannt. Dieses Theorem wird zum Beispiel zur Vereinfachung in der Schaltungsanalyse verwendet.

Berechnung des Norton-Äquivalents

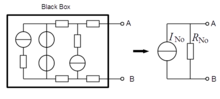
Jede elektrische Schaltung, die ausschließlich aus linearen Spannungsquellen, Stromquellen und Widerständen besteht, kann in ein Norton-Äquivalent umgewandelt werden.

Das Norton-Äquivalent besteht aus einem ohmschen Widerstand $R_{\text{No}}$ und einer Stromquelle mit dem Kurzschlussstrom $I_{\text{No}}$ . Um die zwei Unbekannten $R_{\text{No}}$ und $I_{\text{No}}$ zu bestimmen, werden zwei Gleichungen benötigt. Diese Gleichungen können auf verschiedene Art und Weise aufgestellt werden.

Wenn sich die Schaltung nicht wie eine ideale Spannungsquelle verhält, gilt für $I_{\text{No}}$ :

Der Ausgangsstrom bei Kurzschluss zwischen A und B ist zugleich $I_{\text{No}}$ .

Für $R_{\text{No}}$ gibt es verschiedene Methoden:

Im Schaltbild werden alle Spannungsquellen durch Kurzschlüsse ersetzt und alle Stromquellen durch Unterbrechungen. Die Innenwiderstände der Quellen verbleiben jedoch in der Schaltung. Damit wird der Ersatzwiderstand berechnet. Dieser ist gleich dem Norton-Äquivalentwiderstand.
Ist ein Leerlauf (keine Verbindung von A nach B) zulässig und die Leerlaufspannung $U_{\text{L}}$ bekannt, wird das ohmsche Gesetz benutzt:

$R_{\mathrm {No} }={\frac {U_{\text{L}}}{I_{\mathrm {No} }}}$

Ein bekannter Widerstand wird an A-B angeschlossen und die Stromstärke gemessen. Mit Hilfe des Stromteilergesetzes kann dann $R_{\mathrm {No} }$ bestimmt werden.

Besonders einfach ist die Auswertung, wenn der bekannte Widerstand so einstellbar ist, dass der halbe Kurzschlussstrom durch den Widerstand fließt. Dann ist der eingestellte Widerstand so groß wie $R_{\text{No}}$ .

Der Beweis des Norton-Theorems basiert auf dem Superpositionsprinzip.

Umwandlung zwischen Norton- und Thévenin-Äquivalent

Zwei äquivalente Quellen

Ein Norton-Äquivalent (lineare Stromquelle) und ein Thévenin-Äquivalent (lineare Spannungsquelle) sind gegenseitig äquivalente Quellen. Eine Austauschbarkeit ist unter folgenden zwei Festlegungen gegeben:

Das $R_{{\mathrm i}}$ ist in beiden nebenstehend gezeigten Schaltungen dasselbe (wobei $0<R_{\text{i}}<\infty$ sein muss)
$U_{0}=I_{{\mathrm K}}\cdot R_{{\mathrm i}}$

Frage zum Verständnis

Frage: »In zwei schwarzen Kistchen seien eine Stromquelle mit Parallelwiderstand und eine Spannungsquelle mit Serienwiderstand verborgen, so dass obige Gleichungen erfüllt sind. Kann man von außen feststellen, in welchem schwarzen Kistchen sich die Norton-Schaltung befindet?«

Antwort: Ja! Das Kistchen mit der Norton-Schaltung ist wärmer, denn es nimmt dauernd die Leistung $P_{\mathrm {No} }=I_{\mathrm {No} }^{2}R_{\mathrm {No} }$ auf. Die Thévenin-Schaltung nimmt keine Leistung auf und wird deshalb nicht wärmer. Die Äquivalenz besteht also nur bezüglich der Ausgangsklemmen. Belastet man beide Kistchen jedoch mit einem Kurzschluss, so nimmt das Kistchen mit der Thévenin-Schaltung die Leistung $P_{\mathrm {Th} }={\frac {U_{\mathrm {Th} }^{2}}{R_{\mathrm {Th} }}}$ auf, da nun Strom durch den Thévenin-Widerstand fließt. Die Norton-Schaltung dagegen nimmt keine Leistung mehr auf, da der Norton-Widerstand kurzgeschlossen ist. Die Leistung, die die Norton-Schaltung im offenen Fall aufnimmt, ist gleich groß, wie die Leistung, die von der Thévenin-Schaltung im kurzgeschlossen Fall aufgenommen wird.

Diese Frage bewährt sich, um die Grenzen der Theorie von Norton- und Thévenin-Äquivalent zu verdeutlichen.

Mit diesem Unterschied verbunden ist der Unterschied in den Wirkungsgraden der Spannungsquelle und der Stromquelle, siehe Wirkungsgrad der Stromquelle. Wo immer es auf die Erzielung eines hohen Wirkungsgrades ankommt, sind die Äquivalente nicht austauschbar.

Erweiterung für Wechselstrom

Das Norton-Theorem kann auch auf harmonische Wechselstromsysteme verallgemeinert werden, indem Impedanzen statt der ohmschen Widerstände verwendet werden. Bei Anwendung im Wechselstrombereich ergeben sich jedoch auch Quellen mit frequenzabhängiger Amplitude und Phase. Daher ist eine praktische Anwendung für Wechselstromersatzschaltungen eher selten bzw. auf eine Frequenz beschränkt.

Geschichte

Das Norton-Theorem ist eine Erweiterung des Thévenin-Theorems.

Es wurde 1926 gleichzeitig und unabhängig durch Hans Ferdinand Mayer (1895–1980) (bei Siemens & Halske) und Edward Lawry Norton (1898–1983) (bei Bell Labs) entdeckt. Mayer veröffentlichte seine Entdeckung in der Zeitschrift Telegraphen- und Fernsprech-Technik, Norton publizierte seine Entdeckung in einem internen Arbeitsbericht der Bell Labs.

Literatur

Karl Küpfmüller, W. Mathis, A. Reibiger: Theoretische Elektrotechnik. Springer, Berlin, Heidelberg 2006, ISBN 3-540-29290-X.

Basierend auf einem Artikel in:

Wikipedia.de