Beugungsscheibchen

Berechnetes Beugungsbild im Fernfeld hinter einer Kreisblende. In der Darstellung ist die Intensität logarithmisch auf die Helligkeitsskala umgesetzt. Dies kommt dem realen Eindruck durch das Auge nahe.

Beugungsscheibchen (auch: Beugungsringe) entstehen bei der Beugung eines Lichtstrahls an einer Blende. Ist die Blende kreisförmig, beobachtet man ein zentrales Maximum, umgeben von Ringen abnehmender Licht-Strahlungsintensität. In der Astronomie werden Beugungsscheibchen auch als Airy-Scheibchen (engl. Airy disc) bezeichnet, benannt nach dem englischen Astronomen George Biddell Airy. Nichtkreisförmige Blenden erzeugen gleichfalls Beugungsstrukturen, die sich deutlich von einem Beugungsscheibchen unterscheiden können (Spikes). Mathematisch wird die Beugung von Licht durch das Beugungsintegral beschrieben.

Phänomenologie

Fotografisches Beugungsbild einer mit rotem Laserlicht beleuchteten, 90 Mikrometer großen Lochblende mit 27. Beugungsordnungen

Selbst ein nach den Gesetzen der geometrischen Optik perfektes Instrument, ohne Abbildungsfehler, kann einen als Objekt gegebenen Lichtpunkt nicht genau auf einen Punkt abbilden, sondern durch die Beugung des Lichts an der Apertur entsteht in der Bildebene ein unscharfer Fleck. Die Form des Flecks hängt reziprok von der Form der Apertur ab, insbesondere ist seine Größe umgekehrt proportional zur Größe der Apertur. Bei kreisförmiger Apertur, gegeben etwa durch die runde Fassung einer Linse, ist auch der Fleck rotationssymmetrisch, mit einem zentralen Maximum und schwachen, konzentrischen Ringen. Da die Größe dieses Musters zudem von der Wellenlänge abhängt, sind bei weißem Licht die Beugungsringe kaum zu sehen. Der zentrale Beugungsfleck wird nach dem englischen Astronomen George Biddell Airy auch Airy-Scheibchen genannt.

Versucht man benachbarte Punkte eines Objektes auseinanderzuhalten und erhöht über die Bildweite die Vergrößerung, so wächst zwar der Abstand zwischen den entsprechenden Beugungsbildern, aber auch die Beugungsbilder selber werden im gleichen Verhältnis größer. Man spricht von Beugungsbegrenzung des Winkelauflösungsvermögens. Einfach zu berechnen sind Beugungsbilder für unendliche Bildweite. Das entspricht der Lochkamera und der Fresnelschen Näherung des Beugungsintegrals.

Aufgrund des mit der Blendenöffnung kleiner werdenden Beugungsscheibchens auf der einen Seite und des mit der Blendenöffnung größer werdenden Öffnungsfehlers auf der anderen Seite ergibt sich die größte Bildschärfe bei einer optischen Abbildung bei der kritischen Blende.

Beugung an einer Kreisblende

>Intensität hinter einer kreisförmigen Lochblende

Die Feldstärke E(r) hinter einer mit monochromatischem Licht bestrahlten Lochblende folgt der Funktion

$E(r)=E_{0}\cdot {\frac {2J_{1}(\pi r)}{\pi r}}$

wobei der Abstand vom Punkt maximaler Intensität und $J_{1}(r)$ die Besselfunktion erster Art ist.

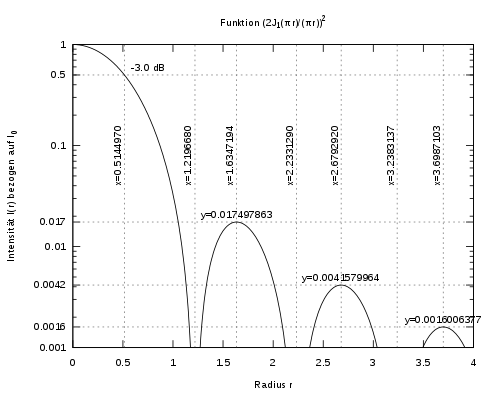
Die Lichtintensität I(r) ~ $E^{2}(r)$ folgt der Funktion

$I(r)=I_{0}\cdot \left({\frac {2J_{1}(\pi r)}{\pi r}}\right)^{2}$

Die Intensität geht in regelmäßigen Abständen auf Null und enthält nach außen schwächer werdende Nebenmaxima. Die Größe der zentralen Beugungsscheibe ergibt sich aus der ersten Nullstelle der Funktion $2J_{1}(\pi r)/(\pi r)$ , die bei $r=1{,}2196\ldots$ liegt.

Beugungsbild einer mit weißem Licht bestrahlten kreisförmigen Lochblende - je kürzer die Wellenlänge $\lambda$ , desto geringer werden die entsprechenden Farbanteile gebeugt

Der Winkel $\theta$ des Randes des zentralen Beugungsscheibchens ergibt sich aus dem Winkelradius zu:

$\sin \,\theta \approx 1{,}220\ \cdot {\frac {\lambda }{D}}$

und für $sin\,\theta =\theta +O(\theta ^{3})$ mit $\theta \ll 1,$

$\theta \approx 1{,}220\cdot {\frac {\lambda }{D}}$

mit

$\lambda$ = Wellenlänge des Lichts und
= Durchmesser der Blende.

Die Funktion $(2J_{1}(\pi r)/(\pi r))^{2}$

hat für den Funktionswert ,
die Standardabweichung des ersten Beugungsscheibchens beträgt $0{,}3950$ ,
hat für $r=0{,}5145$ den Funktionswert (50 % der Intensität),
hat für $r=0{,}7052$ den Funktionswert (25 % der Intensität),
hat bei $r=1{,}2197$ die erste Nullstelle
hat bei $r=1{,}6347$ das erste Nebenmaximum mit dem Funktionswert $0{,}01750$ (1,75 % der Intensität)
hat weitere Nullstellen bei $2{,}2331,\ 3{,}2383,\ \ldots$
hat weitere Nebenmaxima bei $2{,}6793,\ 3{,}6987,\ \ldots$
erhält man in Excel mittels (2*BESSELJ(PI()*x,1)/(PI()*x))^2 mit dem Argument x

Die Größe des Beugungsscheibchens, das sich aus dem effektiven Blendendurchmesser eines optischen Systems ergibt, bestimmt das Auflösungsvermögen. Zwei Punkte lassen sich dann sicher (nach dem Rayleigh-Kriterium) trennen, wenn die Maxima ihrer Abbilder mindestens um den Radius des Beugungsscheibchens auseinander liegen.

Bildet eine Linse aus dem Unendlichen mit der Brennweite ab, hat das zentrale Beugungsscheibchen den Durchmesser $d=\theta \cdot f$

$d=2{,}4392\dots \ \cdot {\frac {\lambda \cdot f}{D}}=2{,}4392\dots \ \cdot \lambda \cdot k$

mit

$\lambda$ = Wellenlänge des Lichtes,
= Brennweite der abbildenden Linse,
= Durchmesser der Linse und
= Blendenzahl

Je größer der Durchmesser beziehungsweise je kleiner die Blendenzahl k=f/D ist, desto kleiner ist der Winkel $\alpha$ beziehungsweise der Durchmesser des Beugungsscheibchens. Daher benötigen hoch auflösende Teleskope große Spiegel.

Näherungsformel zum Abschätzen

In der Praxis rechnet man oft mit folgenden Näherungsformeln (für grünes Licht mit 550 nm Wellenlänge):

d = 1 µm * f / D (Rayleigh-Kriterium ergibt d = 1,34 µm * f / D): Beispiel: eine Blende von f / D = 11 ergibt ein Beugungsscheibchen von 11 µm Durchmesser.

α = 100 mm / D * Winkelsekunden (Rayleigh-Kriterium ergibt α = 140 mm / D * Winkelsekunden): Beispiel: eine Objektivöffnung von D = 100 mm Durchmesser erlaubt eine Winkelauflösung von 1".

Andere Blendenformen

Links Blende, rechts berechnete Beugungsscheibchen.

Detailansicht: Beugungsbild einer Rechteckblende (kleines Bild oben links), Intensität der Nebenmaxima überhöht.

Weicht die Blende von der Kreisform ab, verändert sich die Form des Zentralmaximums und der höheren Beugungsordnungen. Das Bild links zeigt ein Beispiel für eine Rechteck-Blende. Ihre Orientierung ist oben links in der Bildecke angedeutet. Das Verhältnis von Höhe und Breite spiegelt sich auch im Zentralfleck wider, aber mit reziproken Verhältnissen, da Blende und Beugungsbild über die Fourier-Transformation verknüpft sind. Die Nebenmaxima sind am stärksten in den Hauptrichtungen ausgeprägt.

Das Bild rechts zeigt Beugungsscheibchen (rechts) unterschiedlicher Blenden (links). Die ringförmige Helligkeitsmodulation, die man bei einer kreisförmigen Blende erwartet, ist überlagert von strahlenförmigen Sternen, den sogenannten Spikes. Besonders deutlich treten sie bei der Dreiecksblende hervor.

Wird eine Dunkelblende verwendet, ergibt sich im Schatten der entsprechenden Kreisscheibe ebenfalls ein typisches Beugungsbild mit einem Poisson-Fleck in der Mitte.

Beispiele für beugungsbegrenzte Auflösung

Alle Betrachtungen erfolgen, wenn nichts anderes angegeben ist, bei einer im sichtbaren Bereich mittleren Wellenlänge von 555 nm (grün).

Ein beugungsbegrenztes Objektiv mit einer Blendenzahl von 3 erzeugt ein Beugungsscheibchen von zirka 4 µm Durchmesser. Dies ist auf extrem hochauflösenden Schwarz-Weiß-Negativfilmen im Kleinbildformat erkennbar. Bei einer Blendenzahl von 11 hat das Beugungsscheibchen schon einen Durchmesser von knapp 15 µm und ist auf vielen mittelauflösenden Filmemulsionen erkennbar. Gleiches gilt für Bildsensoren mit entsprechenden Pixelrasterabständen.
Wenn die Internationale Raumstation ISS mit einem Objektiv mit 14 cm Durchmesser ausgerüstet ist, lassen sich Details der Größe von 1" auflösen. Bei einer Flughöhe von 350 km entspricht das einer Auflösung von 1,7 m. Um diese Details fotografieren zu können, müssen sie größer als das Auflösungsvermögen des Sensors sein. Wenn dieses 4,8 µm beträgt, ist eine Brennweite von mindestens 1 m erforderlich.
Das Hubble-Weltraumteleskop umkreist die Erde in einer Höhe von 590 km. Sein Spiegel hat einen Durchmesser von 240 cm. Auf die Erde gerichtet hätte es unter optimalen Bedingungen eine Auflösung von 0,17 m.
Große Spiegel sind teuer. Spionagesatelliten kompensieren den Nachteil kleinerer Spiegel mit einer geringen Flughöhe. Bei einem Spiegeldurchmesser von 100 cm und einer Flughöhe von 150 km ist theoretisch eine Auflösung von 0,10 m möglich. Bei Drohnen mit entsprechend geringeren Flughöhen ist trotz noch kleinerer Objektive die erreichbare Auflösung von Objekten an der Erdoberfläche noch höher.
Ein alltäglich beobachtbares Beispiel für Beugungsscheibchen ist die intrinsische Wahrnehmung, also die Wahrnehmung eines Reizes, der im an der Wahrnehmung beteiligten Sinnesorgan selbst seinen Ursprung hat, die durch abgestorbene Zellen im Kammerwasser des Auges entsteht. Blickt man gegen eine helle, möglichst einfarbige Fläche (zum Beispiel gegen den Himmel) so sieht man schwache, transparente Kringel, die langsam nach unten sinken und sich oft zu Ketten zusammenschließen: eben die Beugungsscheibchen, die durch erwähnte im Kammerwasser schwimmende Zellen hervorgerufen werden.

Basierend auf einem Artikel in:

Wikipedia.de