Veranschaulichung einer Singulärwertzerlegung

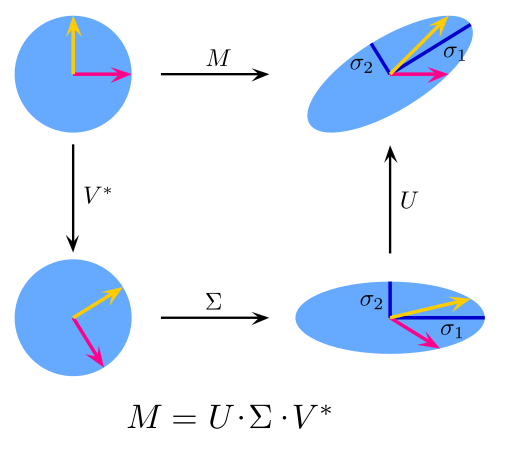
Oben links sieht man den Einheitskreis in blau zusammen mit den Standard-Einheitsvektoren. Oben rechts sieht man das Bild des Einheitskreises unter M: der Kreis wird zu einer Ellipse verzogen. Die SVD zerlegt M in drei einfache Transformationen: eine Rotation V^*, eine Dehnung Σ entlang der Koordinatenachsen und eine zweite Rotation U. Die Zerlegung lässt direkt die Längen σ₁ bzw. σ₂ der großen bzw. kleinen Halbachse der Ellipse erkennen; die Werte stehen in der Hauptdiagonalen von Σ. Die Rotation der Ellipse in Bezug auf das Koordinatensystem wird durch U beschrieben.

In diesem speziellen Fall sieht die Singulärwertzerlegung aus wie folgt::

σ₁ = Φ wobei Φ ≈ 1.618 den Goldenen Schnitt bezeichnet
σ₂ = 1/Φ
V^* = eine Drehung um α im Uhrzeigersinn, wobei tan(α) = Φ, d.h. V ist eine Drehung um −α ≈ −58.28°.
U = eine Drehung gegen den Uhrzeigersinn um β wobei gilt tan(β) = Φ−1, d.h. β ≈ 31.72°.

In der Zerlegung ist nur Σ eindeutig bestimmt; U und V sind es nicht: zu U und V könnten Drehungen um 180° oder Spiegelungen hinzugenommen werden.