Orthogonaltrajektorie
Eine Orthogonaltrajektorie ist in der Mathematik
- eine Kurve, die alle Kurven einer gegebenen Kurvenschar (in der Ebene) senkrecht schneidet.
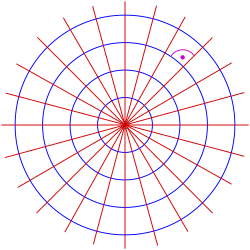
Zum Beispiel sind die Orthogonaltrajektorien einer Schar von konzentrischen Kreisen die Geraden durch den Mittelpunkt der Kreise. Der Teilbereich Differentialgleichung der Mathematik stellt zum Auffinden von Orthogonaltrajektorien geeignete Verfahren zur Verfügung. Beim Standardverfahren bestimmt man zunächst eine gewöhnliche Differentialgleichung 1. Ordnung für die gesuchten Orthogonaltrajektorien und löst diese anschließend mit Hilfe der Methode Trennung der Veränderlichen. Beide Schritte können schwierig bis unlösbar sein. Dann muss man auf numerische Verfahren zurückgreifen.
Orthogonaltrajektorien spielen z. B. in der Physik (Elektrostatik) eine Rolle als Feldlinien in einem elektrischen Feld. Sie stehen senkrecht auf den Äquipotentiallinien.
Lässt man beim Schnitt der Kurve mit der Kurvenschar beliebige aber feste Winkel zu, erhält man eine Isogonaltrajektorie.
Bestimmung der Orthogonaltrajektorien
In kartesischen Koordinaten
In der Regel geht man davon aus, dass die gegebene Kurvenschar implizit durch eine Gleichung der Form
- (0)
1. Beispiel
2. Beispiel
beschrieben wird, wobei
der Scharparameter ist. Falls die Kurvenschar explizit in der Form
gegeben ist, lässt sie sich auch durch
implizit beschreiben. Für die im Folgenden nötigen Ableitungen wird immer still
schweigend vorausgesetzt, dass sie existieren.
- 1. Schritt
Durch implizites Differenzieren nach x ergibt sich
- (1)
im 1. Beispiel
2. Beispiel
- 2. Schritt
Nun wird vorausgesetzt, dass man die Gleichung (0) nach dem Parameter
auflösen kann und damit
aus (1) eliminieren kann. Es entsteht dann eine Differentialgleichung erster
Ordnung der Form
- (2)
im 1. Beispiel
2. Beispiel
die von der gegebenen Kurvenschar erfüllt wird.
- 3. Schritt
Da die Steigung der Orthogonaltrajektorie im Punkt
der negative
Kehrtwert der Steigung der gegebenen Kurve in diesem Punkt sein muss, gilt
für die Orthogonaltrajektorie die Differentialgleichung
- (3)
im 1. Beispiel
2. Beispiel
- 4. Schritt
Diese Dgl. versucht man mit einem der zur Verfügung stehenden Verfahren zu
lösen.
In beiden Beispielen ist Trennung
der Veränderlichen geeignet. Als Lösung
im 1. Beispiel ergeben sich
die Geraden
und
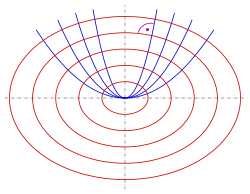
im 2. Beispiel die Ellipsen
In Polarkoordinaten
Liegt die gegebene Kurvenschar in Polarkoordinaten implizit durch
- (0p)
vor, so bestimmt man wie im kartesischen Fall die dazu gehörige parameterfreie Dgl.
- (1p)
- (2p)
der Kurvenschar. Die Dgl. der Orthogonaltajektorien in Polarkoordinaten ist dann (s. Heuser, S. 120)
- (3p)
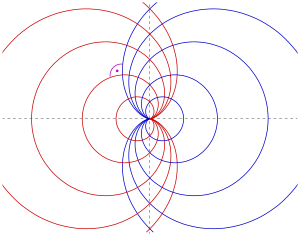
Beispiel: Kardioiden:
- (0p)
(im Bild: blau)
- (1p)
Elimination von
ergibt die Dgl. der gegebenen Schar:
- (2p)
Die Dgl. der Orthogonaltrajektorien ist dann:
- (3p)
Nach Lösen dieser Dgl. mit Trennung der Veränderlichen ergibt sich schließlich
Dies ist die Kardioidenschar (im Bild rot), die durch Spiegelung der gegebenen Schar an der y-Achse entsteht.
Isogonaltrajektorie
- Eine Kurve, die die Kurven einer gegebenen Kurvenschar in einem festen
Winkel
schneidet, nennt man Isogonaltrajektorie.
Für eine Isogonaltrajektorie zum Winkel
besteht im Punkt
zwischen der Steigung
der Kurve (der Schar) und der Steigung
der Trajektorie die Beziehung:
Dies folgt aus dem Additionstheorem
des Tangens, denn der Steigungswinkel der Trajektorie ist um
größer als der der gegebenen Kurve. Für
ergibt sich die Bedingung für die Orthogonaltrajektorie.
Zur Bestimmung der Isogonaltrajektorien einer Kurvenschar muss in der obigen Anleitung nur der 3. Schritt angepasst werden.
- 3. Schritt (Isog.-Traj.)
Die Differentialgleichung der Isogonaltrajektorie ist:
- (3i)
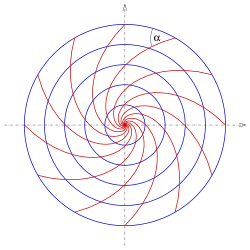
Im 1. Beispiel ergibt sich für den Schnittwinkel
- (3i)
Dies ist eine Ähnlichkeitsdifferentialgleichung,
die mit der Substitution
in eine separierbare
Dgl. übergeführt und gelöst werden kann. Nach Rücksubstitution erhält man
als Gleichung für die Lösungskurven:
In Polarkoordinaten vereinfacht sich diese zu
Dies Gleichung beschreibt logarithmische Spiralen (s. Bild).
Numerische Verfahren
Falls die auftretende Differentialgleichung der Trajektorien mit den theoretischen Verfahren nicht lösbar ist, muss man auf numerische Verfahren zum Lösen einer gewöhnlichen Dgl 1. Ordnung zurück greifen: z. B. auf das Runge-Kutta-Verfahren.
Siehe auch
Literatur
- K. Meyberg,P. Vachenauer: Höhere Mathematik 2, Springer-Verlag, 2003, ISBN 978-3-540-41851-1.
- F. Paech: Analysis – anschaulich und anwendungsorientiert, Fachbuchverlag, Leipzig, 2013, ISBN 978-3-446-43175-1.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 12.12. 2021