Polylogarithmus

Der Polylogarithmus ist eine spezielle Funktion, die durch die Reihe

$\operatorname {Li} _{s}(z)=\sum _{k=1}^{\infty }{\frac {z^{k}}{k^{s}}}$

definiert ist. Für s=1 geht der Polylogarithmus in den gewöhnlichen Logarithmus über:

$\operatorname {Li} _{1}(z)=-\ln(1-z)$

In den Fällen s=2 und s=3 spricht man entsprechend von Dilogarithmus bzw. Trilogarithmus. Die Definition gilt für komplexe und mit |z|<1 . Durch analytische Fortsetzung lässt sich diese Definition auf weitere ausdehnen.

In den wichtigsten Anwendungsfällen ist s=n eine natürliche Zahl. Für diese Fälle kann man den Polylogarithmus rekursiv durch

$\operatorname {Li} _{0}(z)={\frac {z}{1-z}}$

$\operatorname {Li} _{n}(z)=\int _{0}^{z}{\frac {\operatorname {Li} _{n-1}(t)}{t}}\,{\text{d}}t\quad {\mbox{für}}\quad n=1,2,3,\dotsc$

definieren, wonach der Dilogarithmus ein Integral des Logarithmus ist, der Trilogarithmus ein Integral des Dilogarithmus und so fort. Für negative ganzzahlige Werte von lässt sich der Polylogarithmus durch rationale Funktionen ausdrücken.

Der Polylogarithmus taucht beispielsweise im Zusammenhang mit der Fermi-Dirac-Verteilung und der Bose-Einstein-Verteilung auf. Zudem kann mit ihm im hexadezimalen Zahlensystem eine beliebige Stelle von polylogarithmischen Konstanten (z.B. $\pi$ ) einzeln berechnet werden.

Funktionswerte und Rekursionen

Graphen einiger ganzzahliger Polylogarithmen

Einige explizite Funktionsterme für spezielle ganzzahlige Werte von :

$\operatorname {Li} _{1}(z)=-\ln \left(1-z\right)$

$\operatorname {Li} _{0}(z)={\frac {z}{1-z}}$

$\operatorname {Li} _{-1}(z)={\frac {z}{(1-z)^{2}}}$

$\operatorname {Li} _{-2}(z)={\frac {z(1+z)}{(1-z)^{3}}}$

$\operatorname {Li} _{-3}(z)={\frac {z(1+4z+z^{2})}{(1-z)^{4}}}$

$\operatorname {Li} _{-4}(z)={\frac {z(1+z)(1+10z+z^{2})}{(1-z)^{5}}}$

Formal kann man $\operatorname {Li} _{-n}(z):=(z{\tfrac {\text{d}}{{\text{d}}z}})^{n}H(z)$ mit der (für alle divergierenden) Reihe $\textstyle H(z)=\sum _{k=-\infty }^{\infty }z^{k}$ definieren. Obwohl diese Reihe nicht konvergiert, kann diese Definition zum Beweis von Funktionalgleichungen (im Ring der formal definierten Laurent-Reihen) verwendet werden.

Für alle ganzzahligen nichtpositiven Werte von kann der Polylogarithmus als Quotient von Polynomen geschrieben werden. In diesen Fällen ist er also eine rationale Funktion. Für die drei kleinsten positiven Werte von sind im Folgenden die Funktionswerte an der Stelle 1/2 angegeben:

$\operatorname {Li} _{1}\left({\tfrac {1}{2}}\right)=\ln 2$

$\operatorname {Li} _{2}\left({\tfrac {1}{2}}\right)={\tfrac {1}{12}}\left(\pi ^{2}-6\,\ln ^{2}2\right)$

$\operatorname {Li} _{3}\left({\tfrac {1}{2}}\right)={\tfrac {1}{24}}\left(4\,\ln ^{3}2-2\pi ^{2}\,\ln 2+21\,\zeta (3)\right)$

$\zeta$ ist dabei die Riemannsche Zetafunktion. Für größeres sind keine derartigen Formeln bekannt.

Es gilt

$\operatorname {Li} _{s}(1)=\zeta (s)$

und

$\operatorname {Li} _{s}(-1)=-\eta (s)$

mit der dirichletschen $\eta$ -Funktion.

Verschiedene Polylogarithmusfunktionen in der komplexen Ebene

$\operatorname {Li}_{{-3}}(z)$	$\operatorname {Li}_{{-2}}(z)$	$\operatorname {Li}_{{-1}}(z)$	$\operatorname {Li}_{{0}}(z)$

$\operatorname {Li}_{{1}}(z)$	$\operatorname {Li}_{{2}}(z)$	$\operatorname {Li}_{{3}}(z)$

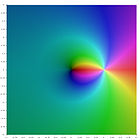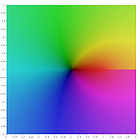Ableitung

Die Ableitung der Polylogarithmen sind wieder Polylogarithmen:

${\frac {\text{d}}{{\text{d}}x}}\operatorname {Li} _{n}(x)={\frac {1}{x}}\operatorname {Li} _{n-1}(x)$

Integraldarstellung

Der Polylogarithmus lässt sich für alle komplexen z,s durch

$\operatorname {Li} _{s}(z)={\frac {z}{2}}+\ln ^{s-1}\,{\frac {1}{z}}\,\Gamma (1-s,-\ln \,z)+2z\int _{0}^{\infty }{\frac {\sin(s\arctan t-t\,\ln \,z)}{(1+t^{2})^{s/2}(\mathrm {e} ^{2\pi \,t}-1)}}\,{\text{d}}t$

mit Hilfe des Integralausdrucks für die Lerchsche Zeta-Funktion darstellen. Dabei ist $\textstyle \Gamma (s,z)=\int _{z}^{\infty }t^{s-1}\mathrm {e} ^{-t}\,{\text{d}}t$ die unvollständige Gammafunktion der unteren Grenze.

Verallgemeinerungen

Mehrdimensionale Polylogarithmen

Die mehrdimensionalen Polylogarithmen sind folgendermaßen definiert:

$\operatorname {L} _{a_{1},\dotsc ,a_{m}}(z)=\sum _{n_{1}>\dotsb >n_{m}>0}{\frac {z^{n_{1}}}{n_{1}^{a_{1}}\dotsb n_{m}^{a_{m}}}}$

Lerchsche Zeta-Funktion

Der Polylogarithmus ist ein Spezialfall der transzendenten Lerchschen Zeta-Funktion:

$\operatorname {Li} _{s}(z)=z\cdot \Phi (z,s,1)$

Nielsens verallgemeinerte Polylogarithmen

Nielsen fand folgende Verallgemeinerung für den Polylogarithmus:

$\operatorname {S} _{n,p}(z)={\frac {(-1)^{n+p-1}}{(n-1)!p!}}\int \limits _{0}^{1}{\frac {\left(\ln(t)\right)^{n-1}\left(\ln(1-zt)\right)^{p}}{t}}{\text{d}}t$

Es gilt:

$\operatorname {S} _{n-1,1}(z)=\operatorname {Li} _{n}(z)$

Basierend auf einem Artikel in:

Wikipedia.de