
Bild (Mathematik)
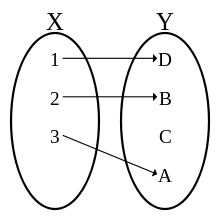
{A, B, D}
Bei einer mathematischen
Funktion
ist das Bild, die Bildmenge oder der Bildbereich einer Teilmenge
des Definitionsbereichs
die Menge der Werte aus der Zielmenge
,
die
auf
tatsächlich annimmt.
Häufig werden dafür auch die Wörter Wertemenge
oder Wertebereich
benutzt, die aber bei anderen Autoren zur Bezeichnung der ganzen Zielmenge
verwendet werden.
Definition
Üblichste Notation
Für eine Funktion
und eine Teilmenge
von
bezeichnet man die folgende Menge als das Bild von M unter f:
Das Bild von f ist dann das Bild der Definitionsmenge unter ,
also:
Im Allgemeinen nutzt man die übliche Mengennotation, um die Bildmenge darzustellen, in obigem Beispiel:
Alternative Notationen
- Für
wird auch die Notation
verwendet, um kenntlich zu machen, dass
nicht auf
als Ganzem, sondern elementweise auf die Mitglieder dieser Menge anzuwenden ist. Als weitere Bezeichnungsweise kommt gelegentlich
vor.
- Für
ist auch die englische Bezeichnung
(„im“ vom englischen Wort image) gebräuchlich.
Beispiele
Wir betrachten die Funktion
(ganze
Zahlen) mit
.
- Hierbei werden verschiedene Eingabemengen nicht unbedingt auf verschiedene Bildmengen geschickt:
- Insgesamt ist die Menge der Quadratzahlen das Bild der Funktion:
Eigenschaften
Es sei
eine Funktion und
und
seien Teilmengen von
:
Die Aussagen über Vereinigung und Durchschnitt lassen sich von zwei Teilmengen auf beliebige nichtleere Familien von Teilmengen verallgemeinern.
Siehe auch


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 09.01. 2022