Fokalkegelschnitt

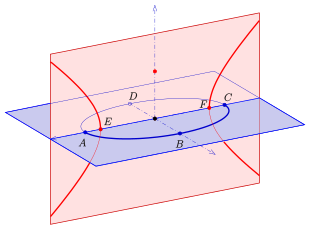
Fokalkegelschnitte: Ellipse, Hyperbel
A,C: Hauptscheitel der Ellipse und Brennpunkte der Hyperbel
E,F: Brennpunkte der Ellipse und Scheitel der Hyperbel

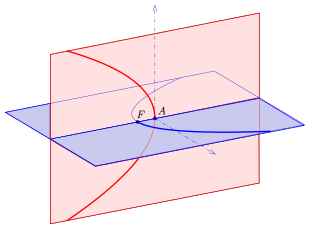
Fokalkegelschnitte: zwei Parabeln
A: Scheitel der roten Parabel und Brennpunkt der blauen Parabel
F: Brennpunkt der roten Parabel und Scheitel der blauen Parabel

In der Geometrie sind Fokalkegelschnitte ein Kurvenpaar bestehend aus entweder

einer Ellipse und einer Hyperbel, wobei die Hyperbel in einer zur Ellipsenebene senkrechten Ebene liegt und deren Scheitel die Brennpunkte der Ellipse und deren Brennpunkte die Hauptscheitel der Ellipse sind (siehe Bild).

oder

zwei Parabeln in zueinander senkrechten Ebenen, wobei der Scheitel der einen der Brennpunkt der anderen ist.

Fokalkegelschnitte ergeben sich in natürlicher Weise bei der Beantwortung der Frage „Welche Rotationskegel enthalten als Schnitt eine vorgegebene Ellipse bzw. Hyperbel bzw. Parabel?“ (siehe unten)

Weiterhin spielen sie in der Geometrie eine wesentliche Rolle

bei der Erzeugung von Dupinschen Zykliden. Sie sind dort Leitkurven für die Darstellung einer Zyklide als Kanalfläche.
bei der Fadenkonstruktion von 3-achsigen Ellipsoiden.

In der physikalischen Chemie verwendet man Fokalkegelschnitte (engl.: focal conics) bei der Beschreibung von geometrischen Eigenschaften von Flüssigkristallen.

Man sollte Fokalkegelschnitte nicht mit konfokalen Kegelschnitten verwechseln. Bei letzteren haben alle Kegelschnitte dieselben Brennpunkte.

Gleichungen und Parameterdarstellungen

Ellipse und Hyperbel

Gleichungen

Beschreibt man die Ellipse in der x-y-Ebene wie üblich durch die Gleichung

${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1\;,$

genügt die zugehörige Fokalhyperbel in der x-z-Ebene der Gleichung

${\frac {x^{2}}{c^{2}}}-{\frac {z^{2}}{b^{2}}}=1\;,$

wobei die lineare Exzentrizität der Ellipse ist, d.h. es gilt $\;c^{2}=a^{2}-b^{2}\;.$

Parameterdarstellungen: Ellipse: $\quad {\vec {u}}(\varphi )=(a\cos \varphi ,b\sin \varphi ,0)^{T}\$ und; Hyperbel: $\ {\vec {v}}(\psi )=(c\cosh \psi ,0,b\sinh \psi )^{T}\ .$

Zwei Parabeln

Zwei Parabeln in der x-y-Ebene bzw. x-z-Ebene:

1. Parabel: $\ y^{2}=p^{2}-2px\$ und

2. Parabel: $\ z^{2}=2px\ .$

Dabei ist der Halbparameter der beiden Parabeln.

Kreiskegel (grün) durch eine Ellipse (blau)

Rotationskegel durch eine Ellipse bzw. eine Hyperbel

Die Spitzen der Rotationskegel durch eine vorgegebene Ellipse (Hyperbel) liegen auf der zur Ellipse (Hyperbel) gehörenden Fokalhyperbel (Fokalellipse).

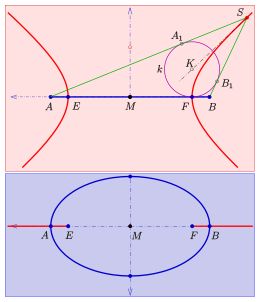
oben: Rotationskegel (grün, Spitze S) durch die Ellipse (blau),
k: Dandelinsche Kugel (lila, Mittelpunkt K)

Nachweis

Gegeben: Ellipse mit Hauptscheitel A,B und Brennpunkten $E,F$ und ein die Ellipse enthaltender Rotationskegel (im Bild grün) mit Spitze .

Aus Symmetriegründen muss die Rotationsachse des Kegels in der zur Ellipsenebene senkrechten Ebene durch die Hauptachse der Ellipse liegen. Es gibt eine Dandelinsche Kugel , die die Ellipsenebene in dem Brennpunkt und den Kegel in einem Kreis berührt. Mit Hilfe des Bildes und der Tatsache, dass alle tangentialen Abstände eines Punktes von einer Kugel gleich sind, erkennt man:

$|AS|=|AA_{1}|+|A_{1}S|=|AF|+|B_{1}S|$

$|BS|=|BB_{1}|+|B_{1}S|=|BF|+|B_{1}S|$

Also ist:

$|AS|-|BS|=|AF|-|BF|=|EF|=const.$

und die Menge aller möglichen Kegelspitzen liegen auf der Hyperbel mit den Scheiteln $E,F$ und den Brennpunkten A,B .

Lässt man die Kegelspitze ins Unendliche wandern, geht der Kegel in einen Zylinder über mit der Asymptote der Hyperbel als Achse und mit der kleinen Ellipsenhalbachse (= kleine Hyperbelhalbachse) als Radius.

Analog beweist man den Fall, dass eine Hyperbel gegeben ist.

Schnitt der Kegel durch Fokalkegelschnitte

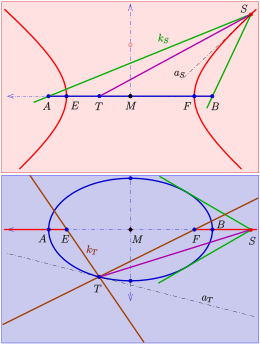
Orthogonale Kegel (grün, braun) durch ${\overline {ST}}$ (lila)

Die einem Paar von Fokalkegelschnitten zugeordneten senkrechten Kreiskegel durch die Kegelschnitte (s. vorigen Abschnitt) spielen bei der Anwendung des Satzes von Dupin auf Dupinsche Zykliden eine wichtige Rolle. Denn es gilt

Wählt man einen beliebigen Punkt der Hyperbel und einen beliebigen Punkt der Ellipse und ist $k_{S}$ der Kreiskegel (grün) durch die Ellipse mit Spitze und $k_{T}$ der Kreiskegel (braun) durch die Hyperbel mit Spitze , so schneiden sich beide Kegel in der gemeinsamen Gerade ${\overline {ST}}$ senkrecht.

Der Schlüssel zum Beweis liegt in der Tatsache, dass die Kegelachse $a_{S}$ von $k_{S}$ die Tangente an die Hyperbel im Punkt ist. Analog gilt: Die Achse a_T des Kegels $k_{T}$ ist Tangente an die Ellipse in . Beide Aussagen folgen aus den Brennstrahleigeneschaften einer Ellipse bzw. Hyperbel (siehe Bild).

Da es sich um senkrechte Kreiszylinder handelt, genügt es zu zeigen, dass die Normalebenen der Kegel durch ${\overline {ST}}$ sich orthogonal schneiden:

Ist

$S:{\vec {s}}=(c\cosh \psi ,0,b\sinh \psi )^{T}\$ und $\ T:{\vec {t}}=(a\cos \varphi ,b\sin \varphi ,0)^{T}\$ , so ist

${\vec {s}}'=(c\sinh \psi ,0,b\cosh \psi )^{T}\$ und $\ {\vec {t}}'=(-a\sin \varphi ,b\cos \varphi ,0)^{T}\$ .

Es gilt: $\ c^{2}=a^{2}-b^{2}\$ (s. oben).

Es ist nachzuweisen, dass die Normalenvektoren der beiden Normalebenen senkrecht zueinander stehen, d.h., dass

$({\vec {s}}'\times ({\vec {s}}-{\vec {t}}))\cdot ({\vec {t}}'\times ({\vec {s}}-{\vec {t}}))=0\$ ist.

Beim Nachrechnen kann man das Kreuzprodukt mit Hilfe der Lagrange-Identität vermeiden:

$({\vec {s}}'\times ({\vec {s}}-{\vec {t}}))\cdot ({\vec {t}}'\times ({\vec {s}}-{\vec {t}}))=({\vec {s}}'\cdot {\vec {t}}')\;({\vec {s}}-{\vec {t}})^{2}-({\vec {t}}'\cdot ({\vec {s}}-{\vec {t}}))\;({\vec {s}}'\cdot ({\vec {s}}-{\vec {t}}))\$

Literatur

Georg Glaeser, Hellmuth Stachel, Boris Odehnal: The Universe of Conics, Springer, 2016, ISBN 3662454505.
E. Müller, E. Kruppa: Lehrbuch der darstellenden Geomelrie, Springer-Verlag, Wien, 1961, ISBN 978-3-211-80589-3.

Basierend auf einem Artikel in:

Wikipedia.de