Helmholtzschicht
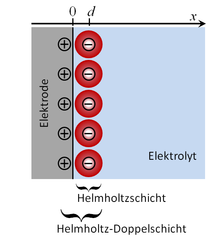
Eine Helmholtzschicht ist ein schmaler Bereich innerhalb eines Elektrolyten, der direkt an eine Elektrode angrenzt und der eine Überschussladung trägt. Das ist möglich, wenn die Summe der Ladung der Kationen nicht gleich der Summe der Ladung der Anionen in diesem Bereich ist. Im einfachsten Fall gibt es einwertige Kationen und einwertige Anionen in unterschiedlicher Zahl. Zur Helmholtzschicht gehören nur die Ionen, die entweder ohne Hydrathülle direkt an der Elektrode anliegen oder die maximal durch eine Hydrathülle von der Elektrode getrennt sind. Die Helmholtzschicht ist nur ein Teil der gesamten elektrochemischen Doppelschicht, die sich mit ihrem diffusen Teil weit in den Elektrolyten erstrecken kann.
Die Helmholtz-Doppelschicht besteht aus der genannten Helmholtzschicht und der entgegengesetzt geladenen Schicht in der Elektrode.
Die Innere Helmholtzebene ist eine Ebene parallel zur Elektrodenoberfläche durch die Schwerpunkte der ohne Hydrathülle direkt an der Elektrode anliegenden Ionen. Solche Ionen nennt man spezifisch adsorbiert. Die Äußere Helmholtzebene ist eine Ebene parallel zur Elektrodenoberfläche durch die Mittelpunkte der Ionen, deren Hydrathülle direkt an der Elektrodenoberfläche anliegen, sie sind nicht spezifisch adsorbiert.
Wegen der festgelegten Abstände der Helmholtzebenen und als Gegensatz zum diffusen Teil der Doppelschicht nennt man die Helmholtz-Doppelschicht auch starre Doppelschicht. Das bedeutet aber nicht, dass sich die Ionen nicht bewegen würden: Sie diffundieren sowohl in der Ebene als auch im Austausch mit der diffusen Doppelschicht. Im Rahmen des Modells von Otto Stern nennt man die Helmholtzschichten auch innere Stern-Schicht.

Historisches
Der Begriff der „Doppelschicht“ stammt von Hermann von Helmholtz. Ohne auf die Grenzfläche Elektrode-Elektrolyt explizit hinzuweisen schrieb er 1853: „Ich werde im Folgenden unter einer elektrischen Doppelschicht stets nur solche zwei Schichten verstehen, welche an den entgegengesetzten Seiten einer Fläche in unendlich kleiner Entfernung vor ihr liegen, und deren eine ebenso viele positive Elektrizität enthält, als die andere negative.“ In einer 1879 veröffentlichten Arbeit erläutert Helmholtz, dass an „metallische Elektroden in einem Electrolyten“ „electrische Doppelschichten an den Electrodenflächen ausbilden, deren electrisches Moment dem zur Zeit vorhandenen Potentialsprunge zwischen der betreffenden Electrode und der Flüssigkeit entspricht“. 1882 veröffentlichte Helmholtz eine Studie der Doppelschicht mit der Quecksilbertropfelektrode, in der er schreibt: „Dehnung der Fläche verdünnt die vorhandene elektrische Doppelschicht derselben und vermindert damit den Potentialunterschied zwischen Quecksilber und Elektrolyten.“
Die Begriffe „innere“ und „äußere“ Ebene wurden vom amerikanischen Chemiker David C. Grahame, der am Amherst College arbeitete, geschaffen und geprägt. Er wies auch darauf hin, dass im Falle kleiner Kationen und großer Anionen die „innere“ Ebene mit den spezifisch adsorbierten Ionen außerhalb der „äußeren“ mit den hydratisierten Kationen liegen kann.
Berechnung des Potentialverlaufs
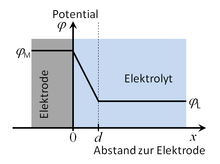
Für den Zusammenhang zwischen Raumladungsdichte ρ und dem Potential φ gilt, wenn man das Potential als Funktion der Koordinate x senkrecht zur Elektrodenoberfläche betrachtet, die Poissongleichung
.
Da zwischen der Elektrodenoberfläche und der inneren Helmholtz-Ebene keine Ladungsdichte auftritt, gilt dort ρ = 0. Daraus folgt die Laplacegleichung
.
Dies bedeutet, dass sich das Potential zwischen der Elektrodenoberfläche und der inneren Helmholtz-Ebene linear ändert.
Auch im Inneren des Metalls tritt keine Ladung auf (ρ = 0). Auch im Inneren des Elektrolyten ist trotz der Anionen und Kationen die mittlere Ladungsdichte Null (ρ = 0); in diesen Fällen ist die Änderung nicht nur konstant, sondern Null. Anhand dieser Randbedingungen erhält man für den Potentialverlauf:
Durchmesser der Schicht und elektrische Feldstärke
Helmholtz schrieb zum Durchmesser der Schicht: „Kohlrausch’s Untersuchungen über die Capicität von Platinflächen bei der Electrolyse des Wassers ergeben den mittlern Abstand solcher Schichten gleich dem 2 475 000sten Theil eines Millimeters, wenn man die Polarisation auf beide Platten gleichmässig vertheilt annimmt“. Dies ist ein Abstand d von 0,40 nm. Das stimmt recht gut mit typischen Ionenradien überein, z.B. 0,17 nm für Chlorid, 0,18 nm für Bromid. Der effektive Durchmesser des Sulfations wird mit 0,40 nm angegeben, der des hydratisierten Natriumions Na+ mit 0,45 nm.
Die Radien der meisten einfachen Ionen liegen im Bereich von 0,1 nm bis 1 nm, selbst dann, wenn sie hydratisiert sind. Damit erwartet man auch, dass der Abstand zwischen Elektrode und Helmholtzebene im Bereich von 0,1 nm bis 1 nm liegt. Elektrochemische Spannungen können wegen der Zersetzungsspannung des jeweiligen Elektrolyts, die für Wasser 1,23 V beträgt, wenige Volt nicht überschreiten. Mit einer Spannung von 0,1 V bis 1 V ergeben sich deswegen elektrische Feldstärken im Bereich von 108 bis 1010 V/m. Diese Werte liegen oberhalb der Durchschlagsfestigkeit vieler Materialien, z.B. beträgt die von Glas nur 107 V/m, die von Wasser 7 107 V/m. Das bedeutet, dass aus makroskopischen Experimenten erhaltene Werte der Durchschlagfestigkeit auf atomarer Skala nicht ohne weiteres angewendet werden können. Die hier auftretenden Spannungen sind aufgrund der kleinen Abstände klein.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 17.11. 2021