Abzählbares Auswahlaxiom

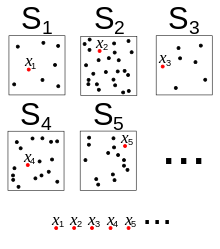
Jede Menge in der abzählbaren Folge von Mengen $(S_{i})_{i}$ enthält mindestens ein Element. Das Axiom von der abzählbaren Auswahl erlaubt es aus jeder Menge gleichzeitig ein Element auszuwählen.

Das abzählbare Auswahlaxiom, auch Axiom von der abzählbaren Auswahl genannt, (von englisch axiom of countable choice, daher kurz AC_ω, für die Bedeutung des Symbols ω siehe Ordinalzahlen) ist eine schwache Form des Auswahlaxioms, das besagt, dass jede abzählbare Menge nichtleerer Mengen eine Auswahlfunktion besitzt.

Das Axiom der abhängigen Auswahl (DC) Impliziert das abzählbare Auswahlaxiom, die Umkehrung gilt nicht.

ZF + AC_ω genügt, um nachzuweisen, dass die abzählbare Vereinigung abzählbarer Mengen wieder abzählbar ist. Ebenso genügt es, um zu zeigen, dass jede unendliche Menge Dedekind-unendlich ist.

AC_ω ist insbesondere bei der Ausarbeitung der Analysis nützlich, wo Ergebnisse oftmals davon abhängen, aus einer abzählbaren Menge von Teilmengen der reellen Zahlen auszuwählen. Beispielsweise um zu zeigen, dass jeder Häufungspunkt einer Folge reeller Zahlen der Grenzwert einer Teilfolge ist, wird sogar nur eine schwächere Form von AC_ω gebraucht. Für allgemeine metrische Räume ist die Aussage sogar äquivalent zu AC_ω.

Formulierung

Folgendermaßen kann das abzählbare Auswahlaxiom formuliert werden, die logischen Äquivalenzen ergeben sich leicht:

Ist eine abzählbare Menge nichtleerer Mengen, so gibt es eine Funktion $f\colon A\to \bigcup A$ mit $f(a)\in a.$ (Eine Funktion mit dieser Eigenschaft nennt man eine Auswahlfunktion.)
Das abzählbare kartesische Produkt nichtleerer Mengen ist nicht leer.
Ist $\left(A_{n}\right)_{n\in \mathbb {\omega } }$ eine Folge nichtleerer Mengen, so gibt es eine Folge $\left(a_{n}\right)_{n\in \mathbb {\omega } }$ mit $a_{n}\in A_{n}.$

Ersetzt man in den ersten beiden Aussagen „abzählbar“ durch „endlich“, so erhält man Aussagen, die ohne Auswahlaxiom, also in ZF beweisbar sind. Lässt man hingegen beliebige Mengen zu, so erhält man das allgemeine Auswahlaxiom.

Natürlich lässt sich zu bestimmten (ggf. auch überabzählbaren) Mengen nichtleerer Mengen eine Auswahlfunktion auch ohne das (abzählbare) Auswahlaxiom angeben, z.B.

wenn der Schnitt $\bigcap A$ nicht leer ist, denn dann gibt es eine konstante Auswahlfunktion,
wenn sich die Vereinigung $\bigcup A$ wohlordnen lässt, denn dann kann jeweils das kleinste Element der Wohlordnung genommen werden, und
wenn es sich um eine Familie von Intervallen von reellen Zahlen handelt, denn dann kann immer das Element in der Mitte genommen werden.

Andererseits kann schon bei einer abzählbaren Familie von zwei-elementigen Mengen die Existenz einer Auswahlfunktion nicht in ZF bewiesen werden.

Folgerungen

Jede unendliche Menge ist auch Dedekind-unendlich

Denn sei unendlich. Für $n\in \mathbb {N}$ sei $A_{n}$ die Menge der $2^{n}$ -elementigen Teilmengen von . Da unendlich ist, sind alle $A_{n}$ nichtleer. Die erste Anwendung von AC_ω liefert eine Folge > $\left(B_{n}\right)_{n\in \mathbb {\omega } }$ , wobei $B_{n}$ eine Teilmenge von mit $2^{n}$ Elementen ist. Die Mengen $B_{n}$ sind nicht notwendigerweise disjunkt, setze jedoch

$C_{n}=B_{n}\setminus \bigcup _{j=0}^{n-1}C_{j}$ .

Offensichtlich enthält jedes $C_{n}$ zwischen einem und $2^{n}$ Elementen und die $C_{n}$ sind disjunkt. Eine weitere Anwendung von AC_ω liefert eine Folge $\left(c_{n}\right)_{n\in \omega }$ , wobei $c_{n}\in C_{n}$ ist.

Somit sind alle $c_{n}$ verschieden und besitzt eine abzählbare Teilmenge. Die Funktion, die $c_{n}$ auf $c_{n+1}$ abbildet und alle anderen Elemente von unverändert lässt, ist injektiv aber nicht surjektiv und beweist, dass Dedekind-unendlich ist.

Die Vereinigung abzählbarer Mengen ist abzählbar

Für eine abzählbare Menge abzählbarer Mengen $\left(A_{n}\right)_{n\in \mathbb {\omega } }$ wähle man für jedes $A_{n}$ eine Funktion $f_{n}$ aus, die $A_{n}$ bijektiv auf $\omega$ abbildet. (Hier wird AC_ω gebraucht.) Die Abbildung

$f:\omega \times \omega \to \bigcup _{n\in \omega }A_{n}$

$f:(n,m)\mapsto f_{n}(m)$ ist surjektiv, daher ist die Vereinigung abzählbar.

Basierend auf einem Artikel in:

Wikipedia.de