Stabilitätstheorie

Die mathematische Stabilitätstheorie beschäftigt sich mit der Entwicklung von Störungen, die als Abweichung von bestimmten Zuständen dynamischer Systeme auftreten. Ein solcher Zustand kann etwa eine Ruhelage oder ein bestimmter Orbit sein, z.B. ein periodischer Orbit.

Neben ihrer theoretischen Bedeutung wird die Stabilitätstheorie in der Physik und in der Theoretischen Biologie angewendet sowie in technischen Gebieten, z.B. in der Technischen Mechanik oder der Regelungstechnik.

Die Lösungsansätze für die Probleme der Stabilitätstheorie sind gewöhnliche und partielle Differentialgleichungen.

Mathematische Stabilitätsbegriffe

Für die Charakterisierung der Stabilität der Ruhelage eines dynamischen Systems $\dot{\vec{x}} = f(\vec{x})$ existieren mehrere Stabilitätsbegriffe mit jeweils etwas unterschiedlicher Aussage:

Eine Ruhelage ${\vec {x}}_{R}$ heißt Ljapunow-stabil, wenn eine hinreichend kleine Störung auch stets klein bleibt. Präziser formuliert: Für jedes $\varepsilon >0$ existiert ein $\delta (\varepsilon )>0$ derart, dass für alle Zeiten $t\geq 0$ und alle Trajektorien ${\vec {x}}(t)$ mit $\|{\vec {x}}(0)-{\vec {x}}_{R}\|<\delta (\varepsilon )$ gilt: $\|{\vec {x}}(t)-{\vec {x}}_{R}\|<\varepsilon$ .
Eine Ruhelage ${\vec {x}}_{R}$ heißt attraktiv, wenn es ein $\eta >0$ derart gibt, dass jede Trajektorie ${\vec {x}}(t)$ mit $\|{\vec {x}}(0)-{\vec {x}}_{R}\|<\eta$ für alle $t\geq 0$ existiert und die folgende Grenzwertbedingung erfüllt: $\lim _{{t\to \infty }}{\vec {x}}(t)={\vec {x}}_{R}.$
Eine Ruhelage heißt asymptotisch stabil, wenn sie Ljapunow-stabil und attraktiv ist.
Eine Ruhelage heißt neutral stabil oder marginal stabil, wenn sie stabil, aber nicht asymptotisch stabil ist.

Für den Fall diskreter Systeme, die durch Differenzengleichungen ${\vec {x}}_{{k+1}}=f({\vec {x}}_{k})$ beschrieben werden, ist die Ruhelage gleichzeitig Fixpunkt der Rekursionsgleichung ${\vec {x}}_{{k+1}}=f({\vec {x}}_{k})$ und es sind ähnliche Stabilitätsdefinitionen üblich.

Lineare zeitinvariante Systeme

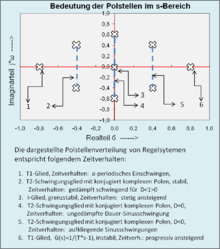
Bedeutung der Pole und der konjugiert komplexen Polpaare in der linken und rechten s-Halbebene

Bei linearen zeitinvarianten Systemen kann die Stabilität an der Übertragungsfunktion durch die Lage der Pole in der s-Ebene abgelesen werden:

Asymptotische Stabilität: wenn sämtliche Pole in der linken s-Halbebene liegen,
Grenzstabilität: wenn kein Pol in der rechten s-Halbebene liegt und mindestens ein einfacher Pol, aber kein mehrfacher Pol, auf der imaginären Achse der s-Halbebene liegt,
Instabilität: sonst (wenn mindestens ein Pol in der rechten s-Halbebene liegt oder wenn mindestens ein mehrfacher Pol auf der imaginären Achse der s-Ebene liegt).

Direkte Methode von Ljapunow und Ljapunow-Funktion

Alexander Michailowitsch Ljapunow entwickelte 1883 die sogenannte Direkte oder Zweite Methode (die Erste Methode war die Linearisierung, siehe unten), um die oben genannten Stabilitätseigenschaften an konkreten Systemen zu überprüfen. Hierzu definiert man zunächst zu einem dynamischen System der Form $\dot{\vec{x}} = f(\vec{x})$ und einer reellwertigen differenzierbaren Funktion $V({\vec {x}})$ die orbitale Ableitung

${\dot {V}}({\vec {x}}):=\left\langle \operatorname {grad}\,V({\vec {x}}),{\dot {{\vec {x}}}}\right\rangle =\left\langle \operatorname {grad}\,V({\vec {x}}),f({\vec {x}})\right\rangle$ .

Eine reellwertige differenzierbare Funktion heißt Ljapunow-Funktion (für das Vektorfeld ), wenn ${\dot V}({\vec {x}})\leq 0$ für alle Punkte ${\vec {x}}$ aus dem Phasenraum gilt. Eine Ljapunow-Funktion ist ein ziemlich starkes Hilfsmittel für einen Stabilitätsbeweis, wie die folgenden beiden Kriterien zeigen:

Erstes Kriterium von Ljapunow: Gegeben sei ein dynamisches System $\dot{\vec{x}} = f(\vec{x})$ . Gelten die Bedingungen

${\vec {x}}_{R}$ ist eine Ruhelage des Systems,
$V({\vec {x}})$ ist eine Ljapunow-Funktion für ,
$V({\vec {x}})$ besitzt an der Stelle ${\vec {x}}_{R}$ ein striktes lokales Minimum,

dann ist die Ruhelage ${\vec {x}}_{R}$ stabil.

Zweites Kriterium von Ljapunow: Gilt zusätzlich zu den Voraussetzungen des ersten Kriteriums noch

4. für ${\vec {x}}\neq {\vec {x}}_{R}$ in einer Umgebung der Ruhelage ${\vec {x}}_{R}$ gilt ${\dot V}({\vec {x}})<0$ ,

dann ist die Ruhelage asymptotisch stabil.

Die Verwendung einer Ljapunow-Funktion nennt man Direkte Methode, weil sich damit direkt aus dem Vektorfeld ohne Kenntnis der Trajektorien (also ohne, dass man die Differentialgleichung lösen müsste) Aussagen über die Stabilität einer Ruhelage gewinnen lassen.

Ljapunowgleichung

Für den Fall linearer Systeme ${\dot {{\vec {x}}}}=A{\vec {x}}$ kann zum Beispiel immer eine positiv definite quadratische Form $v({\vec {x}})={\vec {x}}^{T}R{\vec {x}}$ als Ljapunow-Funktion Verwendung finden. Sie erfüllt offensichtlich die obigen Bedingungen (1) und (2). Bedingung (3) führt auf die Ljapunow-Gleichung

$A^{T}R+RA=-Q$ ,

welche eine spezielle Form der Sylvester-Gleichung ist. Falls positiv definit ist, so ist $v({\vec {x}})={\vec {x}}^{T}R{\vec {x}}$ eine Ljapunow-Funktion. Für stabile lineare Systeme lässt sich eine solche Funktion $v({\vec {x}})={\vec {x}}^{T}R{\vec {x}}$ immer finden.

Stabilitätsanalyse linearer und nichtlinearer Systeme

Ein dynamisches System sei gegeben durch die Differentialgleichung $\dot{\vec{x}} = f(\vec{x})$ .

Wir betrachten eine Störung $\delta ={\vec {x}}(t)-{\vec {x}}_{R}$ zum Zeitpunkt als Abweichung von der Ruhelage ${\vec {x}}_{R}$ :

wenn das System linear ist, kann diese Störung vollständig durch die Jacobi-Matrix ${\mathbf {J}}$ der ersten Ableitungen nach ${\vec {x}}$ ausgedrückt werden.
ist das System nichtlinear und die Störung klein genug, so kann man es "linearisieren", d.h. die Funktion nach $\delta$ um ${\vec {x}}_{R}$ Taylor-entwickeln.

In beiden Fällen ergibt sich für die Zeitentwicklung von $\delta$ :

${\dot {\delta }}=\mathbf {J} ({\vec {x}}_{R})\,\delta$

Diese Entwicklung wird demnach maßgeblich von den Eigenwerten der Jacobi-Matrix bestimmt. Konkret ergeben sich die folgenden drei Fälle:

Der Realteil aller Eigenwerte der Jacobi-Matrix ist negativ. Dann fällt $\delta$ exponentiell ab, und die Ruhelage ist asymptotisch stabil.
Der Realteil eines Eigenwertes der Jacobi-Matrix ist positiv. Dann wächst $\delta$ exponentiell an, und die Ruhelage ist instabil.
Der größte Realteil aller Eigenwerte der Jacobi-Matrix ist Null. Dies bedeutet für ein lineares System:
- falls für alle Eigenwerte mit verschwindendem Realteil die algebraische Vielfachheit gleich der geometrischen Vielfachheit ist: marginale Stabilität der Ruhelage.
- sonst, d.h. falls nicht für alle Eigenwerte mit verschwindendem Realteil die algebraische Vielfachheit gleich der geometrischen Vielfachheit ist: Instabilität der Ruhelage.

Bei nichtlinearen Systemen, die nur um die Ruhelage linearisiert wurden, kann die Stabilität auch noch von Termen höherer Ordnung in der Taylorentwicklung bestimmt werden. In diesem Fall vermag die lineare Stabilitätstheorie keine Aussage zu machen.

Siehe auch Autonome Differentialgleichung.

Beispiel

Ein untersuchter Verformungszustand der Festigkeitslehre oder ein Bewegungszustand der Dynamik können ab einer zu bestimmenden Stabilitätsgrenze in einen anderen Zustand wechseln. Damit verbunden sind in der Regel nichtlinear ansteigende Verformungen oder Bewegungen, die zur Zerstörung von Tragwerken führen können. Um diese zu vermeiden, ist die Kenntnis der Stabilitätsgrenze ein wichtiges Kriterium zur Bemessung von Bauteilen.

Weitere Beispiele:

Stabilitätsprüfung von Regelkreisen,
Dynamik von Insektenpopulationen,
Eulerscher Knickstab,
Kippen von schlanken Trägern,
Beulen von Platten und Schalen,
Wachstum kleiner Störungen in einer Grenzschicht, die zum laminar-turbulenten Umschlag führen.

Siehe auch

Eigenbewegung (Regelungstechnik)
Lineare Stabilitätstheorie zur Stabilitätstheorie in der Strömungslehre

Basierend auf einem Artikel in:

Wikipedia.de