
Gibbssche Phasenregel
Die Gibbssche Phasenregel (nach Josiah Willard Gibbs 1876, auch einfach Phasengesetz) gibt an, wie viele Freiheitsgrade ein im thermodynamischen Gleichgewicht befindliches System in Abhängigkeit von der Zahl der enthaltenen Substanzen und der Zahl der gleichzeitig existierenden Phasen besitzt.
Da die Zahl der Freiheitsgrade nicht kleiner als Null sein kann, trifft die Phasenregel damit auch eine Aussage über die maximale Anzahl von Phasen, die in einem System mit einer gegebenen Anzahl von Substanzen gleichzeitig existieren können.
Aus der Version der Phasenregel für die einfachsten thermodynamischen Systeme lässt sich ableiten, dass für die Beschreibung solcher Systeme über die zur Beschreibung der stofflichen Zusammensetzung nötigen Variablen hinaus nur zwei intensive Zustandsgrößen nötig sind.
Phasenregel
Für die einfachsten thermodynamischen Systeme lautet die Phasenregel:
: Anzahl der Freiheitsgrade des Systems
: Anzahl der unabhängigen Substanzen im System
: Anzahl der Phasen im System
Die Anzahl der Freiheitsgrade ist die Anzahl der intensiven
Zustandsvariablen, die gleichzeitig beliebig geändert werden können, ohne dass
das Gleichgewicht zwischen den Phasen zerstört wird und die Zahl der Phasen des
Systems sich ändert.
Sie ist auch die Anzahl der Variablen, deren Werte
festgelegt werden müssen, wenn das System einen bestimmten vorgegebenen Zustand
annehmen soll.
Die Anzahl der unabhängigen Substanzen (auch: Anzahl der Komponenten) ist in Systemen ohne chemische Reaktionen gleich der Anzahl der im System vorhandenen Substanzen. In Systemen, in denen chemische Reaktionen ablaufen und chemisches Gleichgewicht herrscht, ist sie die Anzahl der im System vorhandenen Substanzen abzüglich der Anzahl der unabhängigen Reaktionen.
Die Zahl 2 ist nur für die einfachsten thermodynamischen Systeme gültig, was aber die meisten Flüssigkeiten und Gase einschließt. Für komplexere Systeme können andere Zahlen auftreten.
Beispiele
In Tabellenform lässt sich die Phasenregel wie folgt darstellen:
| K = 1 | K = 2 | K = 3 | |
|---|---|---|---|
| P = 1 | f = 2 | 3 | 4 |
| P = 2 | 1 | 2 | 3 |
| P = 3 | 0 | 1 | 2 |
| P = 4 | - | 0 | 1 |
Aus der Tabelle folgt für das Beispiel eines einkomponentigen Systems ():
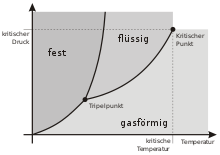
- Liegt im System nur eine Phase vor (
), hat es zwei Freiheitsgrade (
). Sein Zustandspunkt liegt im Phasendiagramm innerhalb einer Phasengebiets-Fläche und ist ringsherum von diesem Phasengebiet umgeben. Er kann sich grundsätzlich (wenn auch vielleicht nur eine kleine Strecke) im Diagramm beliebig sowohl nach oben oder unten wie auch nach links oder rechts bewegen, ohne das Phasengebiet zu verlassen.
Beispiel: Flüssiges Wasser bei Raumtemperatur und Atmosphärendruck bleibt flüssig, auch wenn Temperatur und Druck (um nicht zu große Beträge) unabhängig voneinander in beliebigen Richtungen geändert werden.
- Liegen im System gleichzeitig zwei Phasen vor (
), gibt es genau einen verbleibenden Freiheitsgrad (
). Das System befindet sich im Phasendiagramm auf einer eindimensionalen Koexistenzlinie zwischen zwei Phasengebieten und kann sich, wenn das Gleichgewicht zwischen den Phasen nicht zerstört werden soll, nur entlang dieser Linie bewegen.
Beispiel: Damit flüssiges und dampfförmiges Wasser bei einer gegebenen Temperatur im Gleichgewicht stehen, muss der Druck beider Phasen einen bestimmten Wert haben, nämlich den der Temperatur entsprechenden Gleichgewichtsdampfdruck des Wassers. Ändert man Temperatur und Druck beliebig, verlässt das System im Allgemeinen die Koexistenzlinie und wandert in eines der angrenzenden Phasengebiete, die andere Phase geht verloren (Verdunstung des gesamten Wassers oder Kondensation des gesamten Dampfes). Man kann also nur eine der beiden Variablen beliebig ändern (beispielsweise die Temperatur), die Änderung der anderen kann nicht beliebig erfolgen, sondern muss mit der ersten so abgestimmt sein, dass der neue Zustand nach wie vor auf der Koexistenzlinie liegt.
- Liegen im System gleichzeitig drei Phasen vor (
), so verbleibt kein Freiheitsgrad mehr (
). Das System ist auf einen Punkt im Phasendiagramm beschränkt, den Tripelpunkt. Verlässt es diesen Tripelpunkt, wird das Gleichgewicht zwischen den drei Phasen zerstört und mindestens eine Phase verschwindet.
Beispiel: Wasser kann an seinem Tripelpunkt (Temperatur 273,16 K, Druck 611,7 Pa) gleichzeitig in den Aggregatzuständen fest, flüssig und gasförmig vorliegen. Bei jeder Abweichung vom Tripelpunkt verschwindet mindestens eine der Phasen.
- Es können im System nicht mehr als drei Phasen gleichzeitig vorliegen, weil die Zahl der Freiheitsgrade nicht kleiner als Null werden kann.
Die Anzahl
der gleichzeitig existenzfähigen Phasen in Abhängigkeit von
und
wird in der folgenden Tabelle dargestellt:
| K = 1 | K = 2 | K = 3 | |
|---|---|---|---|
| f = 0 | P = 3 | 4 | 5 |
| f = 1 | 2 | 3 | 4 |
| f = 2 | 1 | 2 | 3 |
| f = 3 | - | 1 | 2 |
Demnach kann es in einem einkomponentigen System ()
maximal drei koexistierende Phasen geben (
),
da die Anzahl der Freiheitsgrade nicht kleiner als Null werden kann.
Entsprechend können in einem zweikomponentigen System (
)
maximal vier Phasen koexistieren (
)
und so weiter.
Erläuterung
Thermodynamischer Zustand
Möchte man den Zustand eines makroskopischen Systems physikalisch vollständig beschreiben, indem man die Orte, Geschwindigkeiten und inneren Zustände aller enthaltenen Moleküle aufzeichnet, läge die Anzahl der zu erfassenden Zahlen in der Größenordnung der Avogadro-Zahl 1023 und damit klar außerhalb praktischer Möglichkeiten. Die Thermodynamik verzichtet auf die vollständige, detaillierte Kenntnis des Zustands und gibt sich mit der Erfassung und Verarbeitung einer wesentlich geringeren Anzahl von Variablen zufrieden. Der „thermodynamische Zustand“ eines Systems, das sich im thermodynamischen Gleichgewicht befindet, lässt sich mit einer kleinen Anzahl von Variablen wie Temperatur, Druck und so weiter vollständig beschreiben. Es stellt sich die Frage, wie viele Variablen dazu mindestens benötigt werden.
Thermodynamische Variablen
Man unterscheidet extensive und intensive thermodynamische Größen. Extensive Größen beschreiben Eigenschaften, die proportional zur Größe des Systems sind. Beispiele sind das Volumen des Systems, seine Masse, oder seine innere Energie. Intensive Größen beschreiben Eigenschaften, die unabhängig von der Größe des Systems sind. Beispiele sind der Druck, die Temperatur, oder die spezifische (also durch die Masse dividierte) innere Energie. Denkt man sich ein homogenes System, in dem eine einheitliche Temperatur und ein einheitlicher Druck herrschen, in zwei halb so große Teilsysteme aufgeteilt, dann sind Masse, Volumen und innere Energie der Teilsysteme als extensive Größen nur halb so groß wie die des Originalsystems. Druck, Temperatur und spezifische innere Energie der Teilsysteme haben als intensive Größen dieselben Werte wie im Originalsystem.
Minimalsatz von Variablen
Zwei intensive Variablen
Wie die Erfahrung zeigt, werden zur vollständigen thermodynamischen Beschreibung der einfachsten geschlossenen Systeme drei Variablen benötigt, wovon mindestens eine eine extensive Variable sein muss. Die extensive Variable liefert Information über die Größe des Systems. Interessiert man sich nur für intensive Eigenschaften des Systems wie beispielsweise dessen Materialeigenschaften, wird keine Information über die Systemgröße benötigt und es genügen zwei intensive Variablen.
Sobald in einem solchen Fall zwei unabhängige intensive Variablen festgelegt
sind, sind damit auch alle anderen intensiven Variablen fixiert, der
„thermodynamische Zustand“ des Systems (außer seiner Größe) ist eindeutig
festgelegt. Wenn beispielsweise von einer Probe Wasser bekannt ist, dass ihre Viskosität
0,506·10−3 N s m−2 beträgt und ihr Brechungsindex den Wert
1,3289 hat, dann folgt daraus, dass ihre Dichte 0,9881 g cm−1
beträgt, ihre Temperatur 50 °C ist, und so weiter.
Ein oft benutztes Variablenpaar sind aufgrund ihrer Praxisnähe der Druck
und die Temperatur
:
Den thermodynamischen Zustand ohne Berücksichtigung der Systemgröße bezeichnet man auch als den „intensiven Zustand“. Bei den Systemen, deren intensiver Zustand bereits durch zwei intensive Variablen vollständig beschrieben werden kann, handelt es sich insbesondere um Systeme, die makroskopisch homogen, isotrop und ungeladen sind, die groß genug sind, so dass Oberflächeneffekte vernachlässigt werden können, und auf die keine elektrischen oder magnetischen Felder und keine Gravitationsfelder einwirken. Solche Systeme besitzen also beispielsweise keine elektrische Ladung und keine elektrischen oder magnetischen Dipol- oder höheren Momente. Es treten keine elastischen Scherspannungen oder ähnliche mechanische Erscheinungen auf. Sie besitzen eine unveränderliche chemische Zusammensetzung.
Zusätzliche Variablen
Kompliziertere Systeme benötigen in der Regel eine größere Anzahl von Variablen. Für die thermodynamische Beschreibung von Festkörpern werden oft zusätzliche Größen benötigt, weil sie Inhomogenitäten, Anisotropien, innere mechanische Spannungen und so weiter aufweisen können. Bei Systemen, die mit der genannten Minimalanzahl von Variablen auskommen, handelt es sich meistens um Fluide, also um Gase oder Flüssigkeiten.
Zusätzliche Variablen werden auch benötigt, wenn das System eine
veränderliche chemische Zusammensetzung besitzt. In diesem Fall könnte die
Zusammensetzung durch Angabe der vorhandenen Mengen der beteiligten
Substanzen beschrieben werden. Solche Mengenangaben sind extensive Größen. Wenn
nur intensive Größen von Interesse sind, bietet es sich an, die Anteile
der einzelnen Substanzen am Gesamtsystem als intensive Variablen zu benutzen.
Für diesen Zweck werden oft die Molenbrüche
der Substanzen verwendet, also ihre jeweilige Molzahl dividiert durch die
Molzahl des Gesamtsystems. Weil die Summe der Molenbrüche ihrer Definition
entsprechend Eins sein muss, genügt bei Vorliegen von
Substanzen die Angabe von
Molenbrüchen. Ein solcher Satz von Molenbrüchen beschreibt die „Zusammensetzung“
des Systems. Ein Variablensatz für ein solches System könnte beispielsweise
sein. Sofern über die Beschreibung der Zusammensetzung hinaus das System nur
die genannten zwei intensiven Variablen benötigt, umfasst der Variablensatz des
Systems
Variablen. Falls das System zwar eine Mischung mehrerer Substanzen enthält, sich
deren Zusammensetzung im Laufe des betrachteten Prozesses aber nicht ändert,
werden auch keine Variablen zur Beschreibung der Zusammensetzung benötigt.
Im Folgenden wird vorausgesetzt, dass das betrachtete System außer gegebenenfalls Variablen zur Beschreibung der Zusammensetzung nur zwei intensive Variablen benötigt. Für andere Systeme muss die Phasenregel individuell angepasst werden.
Einführendes Beispiel
Man betrachte ein System, das aus einer einzigen Substanz besteht, die in
zwei Phasen
und
vorliegt (beispielsweise flüssiges und gefrorenes Wasser). Zur Beschreibung
jeder der Phasen seien zwei intensive Variablen ausreichend, als solche seien
jeweils Temperatur
und Druck
gewählt. Damit beide Phasen im Gleichgewicht stehen, müssen ihre Temperaturen,
Drücke und chemischen
Potentiale dieselben sein. Andernfalls würden Wärmeströme zwischen den
Phasen fließen, bis die Temperaturen ausgeglichen sind, würden sich die Volumina
der Phasen ändern, bis die Drücke ausgeglichen sind, und würde Substanz zwischen
den Phasen ausgetauscht (beispielsweise ein Teil des Wassers schmelzen), bis die
chemischen Potentiale ausgeglichen sind.
Da die chemischen Potentiale
Funktionen von Druck und Temperatur sind, liegen die vier unabhängigen Variablen
,
,
und
vor. Im Gleichgewichtszustand existieren zwischen diesen vier Variablen
drei Gleichungen:
Da die Anzahl der unabhängigen Gleichungen kleiner ist als die Anzahl der unabhängigen Variablen, handelt es sich um ein unterbestimmtes Gleichungssystem. Im vorliegenden Fall kann eine der Variablen frei gewählt werden, die anderen drei sind durch diese Wahl dann eindeutig festgelegt. Im Phasendiagramm des Systems liegt der Zustand auf der Koexistenzlinie, entlang welcher die beiden Phasen koexistieren. Eine andere Wahl der (einen) freien Variablen entspricht einem anderen Ort auf der (eindimensionalen) Koexistenzlinie. Das System hat einen Freiheitsgrad.
Enthält das System eine dritte Phase ,
dann liegen sechs Variablen
,
,
,
,
,
vor, zwischen denen sechs Gleichungen bestehen:
Da jetzt die Anzahl der unabhängigen Gleichungen gleich der Anzahl der unabhängigen Variablen ist, hat das Gleichungssystem genau eine Lösung. Im Gleichgewichtszustand dieses thermodynamischen Systems sind die Werte aller seiner Variablen festgelegt. Keine der Variablen kann frei gewählt werden, ohne das Gleichgewicht zu zerstören. Das System hat keinen Freiheitsgrad. Im Phasendiagramm befindet es sich am Tripelpunkt der betreffenden Substanz.
Die Phasenregel dient dazu, die Anzahl der Freiheitsgrade allgemeiner Systeme zu ermitteln.
Phasenregel für nicht chemisch reagierende Substanzen
Das Interesse gilt im Folgenden ausschließlich intensiven Variablen. Es sei
ein System mit
Substanzen gegeben, die nicht chemisch miteinander reagieren. Es sei zunächst
angenommen, dass in jeder Phase alle Substanzen vorhanden sind. Die
Zusammensetzung jeder Phase wird dann durch
Molenbrüche beschrieben. Zusammen mit Druck und Temperatur umfasst der
Variablensatz für jede Phase insgesamt
Variablen. Es seien
Phasen vorhanden, für das ganze System ist also die
.
Im Gleichgewicht bestehen zwischen diesen Variablen die folgenden Gleichungen:
-
also Gleichungen zwischen den Temperaturen,
also Gleichungen zwischen den Drücken,
also Gleichungen zwischen den chemischen Potentialen von Substanz 1,
also Gleichungen zwischen den chemischen Potentialen von Substanz 2,
... also Gleichungen zwischen den chemischen Potentialen von Substanz
.
Jede dieser
Zeilen enthält
Gleichungen. Es ist daher die
.
Gäbe es keine Gleichungen (Bedingungen) zwischen den Variablen, könnten sie alle unabhängig voneinander variiert werden. Jede der Gleichungen reduziert die Anzahl der Variablen, die unabhängig voneinander variiert werden können, um eins. Die Anzahl der unabhängig variierbaren Variablen (die Anzahl der Freiheitsgrade des Systems) ist daher gleich der Anzahl der Variablen minus der Anzahl der zwischen ihnen bestehenden Gleichungen:
Dies ist die Phasenregel für nicht chemisch reagierende Substanzen.
Falls entgegen der oben genannten Annahme nicht alle Substanzen in jeder Phase vorhanden sind, bleibt das Ergebnis trotzdem dasselbe. Wenn beispielsweise eine Substanz in einer der Phasen nicht enthalten ist (etwa weil sie grundsätzlich in dieser Phase nicht löslich ist), entfällt eine Variable, nämlich der Molenbruch für diese Substanz in dieser Phase. Andererseits entfällt auch eine der Bedingungsgleichungen, nämlich jene, die die Gleichheit des chemischen Potentials der Substanz in dieser Phase mit den chemischen Potentialen der Substanz in den anderen Phasen feststellt (wenn die Substanz in dieser Phase unlöslich ist, ist ihr chemisches Potential in dieser Phase größer als in den anderen Phasen).
Phasenregel für chemisch reagierende Substanzen
Das betrachtete System enthalte nun
Substanzen, von denen einige oder alle chemisch miteinander reagieren und sich
im chemischen Gleichgewicht befinden. Die hier zusätzlich auftretenden
Bedingungen, dass Reaktionsgleichgewichte zwischen den betreffenden Substanzen
herrschen sollen, reduzieren die Freiheitsgrade des Systems weiter. Sei
die Anzahl der unabhängigen chemischen Reaktionen (siehe unten) und
wieder die Anzahl der vorliegenden Phasen.
Wie im vorigen Abschnitt wird der Zustand des Systems beschrieben durch
Temperaturen,
Drücke und
Molenbrüche. Es ist also die
.
Es bestehen wieder
Gleichungen zwischen den Temperaturen,
Gleichungen zwischen den Drücken,
Gleichungen zwischen den chemischen Potentialen der auf
Phasen verteilten
Substanzen (nämlich
Gleichungen für jede der
Substanzen). Zusätzlich kommen jetzt
durch die Reaktionen vermittelte Gleichgewichtsbedingungen zwischen den
chemischen Potentialen hinzu. Also ist die
.
Die Differenz aus der Anzahl der Variablen und der Anzahl der Gleichungen ist wiederum die
Die Phasenregel hat in diesem Fall dieselbe Form wie im vorigen Abschnitt,
nur ist die dortige Anzahl
der nichtreagierenden Substanzen nun ersetzt durch die Anzahl der vorhandenen
Substanzen minus der Anzahl der unabhängigen Reaktionen,
.
Beide Formen der Phasenregel lassen sich durch dieselbe Formel ausdrücken,
wenn die folgende Bezeichnung benutzt wird: Die so genannte „Anzahl der
unabhängigen Substanzen“
ist die Anzahl der vorhandenen Substanzen minus der Anzahl der zwischen ihnen
ablaufenden unabhängigen chemischen Reaktionen.
Falls keine Reaktionen ablaufen, ist die Anzahl der unabhängigen Substanzen
gleich der Anzahl der vorhandenen Substanzen.
Mit diesen Bezeichnungen lautet die Phasenregel für Systeme mit oder ohne chemische Reaktionen:
Falls Reaktionen ablaufen, ist die Anzahl der unabhängigen Substanzen auch die Anzahl der Substanzen, die in das System eingesetzt werden müssen, damit die chemischen Reaktionen aus ihnen alle Substanzen erzeugen können, die im Gleichgewichtszustand des Systems vorhanden sind (siehe unten für ein Beispiel). Die Anzahl der unabhängigen Substanzen heißt daher auch „Anzahl der Komponenten“.
Phasenregel für komplexere Systeme
Abweichende Voraussetzungen
Die in den oben abgeleiteten Phasenregeln auftretende Zahl 2 ergibt sich aus den Annahmen, dass
- der Druck in allen Phasen derselbe ist,
- neben den die Zusammensetzung beschreibenden Variablen genau zwei weitere Variablen zur Beschreibung des Systems benötigt werden (in den Herleitungen wurden dafür Temperatur und Druck gewählt).
Diese Annahmen treffen nicht für alle möglichen Systeme zu. In Systemen, in denen osmotische Drücke auftreten, können auch im Gleichgewicht in verschiedenen Phasen unterschiedliche Drücke herrschen. In komplexeren Systemen können über die Zusammensetzung hinaus mehr als zwei weitere Variablen benötigt werden, etwa eine magnetische Feldstärke. In solchen Fällen muss die Phasenregel entsprechend modifiziert werden. Wenn ein thermodynamisches System gegen die Phasenregel oder ein anderes thermodynamisches Gesetz zu verstoßen scheint, liegt die Ursache oft darin, dass bei der Beschreibung des Systems noch nicht alle wesentlichen Zustandsvariablen berücksichtigt wurden.
Feststoffe
Feststoffe sind ein Beispiel für den Fall, dass eine kleinere Anzahl von Variablen ausreichend sein kann. Bei ihnen hat eine (begrenzte) Änderung des Druckes in der Regel nur geringe und oft vernachlässigbare Auswirkungen. In diesem Fall kann auf die Betrachtung der Variablen Druck verzichtet werden und die Phasenregel lautet, falls keine weiteren Variablen aus anderen Gründen benötigt werden:
Diese Vereinfachung gilt jedoch nicht bei höheren Drücken, wie sie beispielsweise bereits in der Erdkruste vorliegen. Für die Druck- und Temperaturermittlung in der Geothermobarometrie ist dies für die korrekte Erfassung der jeweiligen Gleichgewichts-Paragenese von großer Bedeutung.
Nebenbedingungen
Es kann vorkommen, dass das System zusätzlichen Nebenbedingungen unterworfen ist. Jede dieser Nebenbedingungen erhöht die Gesamtzahl der Bedingungen um eins und verringert dadurch die Anzahl der Freiheitsgrade um eins.
Falls das System beispielsweise dem Atmosphärendruck ausgesetzt ist, besteht über die übliche Gleichgewichtsbedingung hinaus, dass der Druck in allen Phasen derselbe sein muss, zusätzlich die Nebenbedingung, dass dieser Druck gleich dem Atmosphärendruck sein muss. Betrachtet man etwa Wasser, das mit seinem Dampf im Gleichgewicht steht und gleichzeitig durch Kontakt mit der Atmosphäre auf Atmosphärendruck gehalten wird (ein offenes Glas Wasser in einem Raum mit wasserdampfgesättigter Luft), dann ergeben sich mehrere Möglichkeiten zur Beschreibung des Systems:
- Falls der Einfluss des Außendrucks auf das System vernachlässigbar ist,
genügt es, das System als nur aus Wasser bestehend zu betrachten und die
Nebenbedingung zu ignorieren. Es ist dann
und
, also
. Demnach kann – in Übereinstimmung mit der Erfahrung – die Temperatur des Systems frei gewählt werden, der Dampfdruck stellt sich dann auf einen durch die Temperatur bestimmten Wert ein.
Bei der Betrachtung des Gleichgewichtsdampfdrucks von Wasser wird in der Tat meistens der Einfluss des Atmosphärendrucks ignoriert. Die meisten gängigen Dampfdrucktafeln und -formeln setzen voraus, dass nur Wasser (als Flüssigkeit und als Dampf) vorhanden ist und dass der in beiden Phasen herrschende Druck der Gleichgewichtsdampfdruck ist. Unter diesen Bedingungen beträgt beispielsweise bei 20 °C der Gleichgewichtsdampfdruck des Wassers 2339,2 Pa. Stehen Wasser und Dampf hingegen unter Atmosphärendruck, wie es in Alltag und Labor in der Regel der Fall ist, erhöht die Poynting-Korrektur den Gleichgewichtsdampfdruck um den Faktor 1,00072. Diese Korrektur ist für die meisten praktischen Fälle vernachlässigbar.
- Das System kann als zweikomponentig aufgefasst werden: Die beiden
Komponenten sind das Wasser und die Atmosphärenluft, die beiden Phasen sind
das Wasser (mit etwas gelöster Luft) und das Luft/Dampf-Gemisch. Aus
,
und einer zusätzlichen Bedingung (fixer Gesamtdruck) folgt wieder
.
- Das System kann sogar als dreikomponentig aufgefasst werden, bestehend aus
der Flüssigkeit sowie dem Stickstoff und dem Sauerstoff der Atmosphäre. Aus
,
und zwei zusätzlichen Bedingungen (fixer Gesamtdruck, fixes Sauerstoff-Stickstoff-Verhältnis) folgt wieder
.
Eine wichtige Nebenbedingung liegt auch in ionischen Lösungen vor: Die Konzentrationen der Anionen und Kationen beeinflussen sich aufgrund der zwischen ihnen wirkenden Coulomb-Kräfte so, dass die Lösung als Ganzes elektrisch neutral ist.
Unabhängige Reaktionen und Substanzen
Wie die obigen Herleitungen zeigen, ist die Phasenregel nicht Ausdruck speziell chemischer Gesetzmäßigkeiten, sondern folgt aus den mathematischen Eigenschaften von Gleichungssystemen. Aus diesem Zusammenhang erklärt sich auch der Bezug auf „unabhängige“ Reaktionen beziehungsweise Substanzen, die im Folgenden näher erläutert werden.
Anzahl der unabhängigen Gleichungen
Ein lineares Gleichungssystem ist eindeutig lösbar, wenn es ebensoviele Gleichungen wie Variablen (Unbekannte) enthält. Gibt es weniger Gleichungen als Unbekannte, kann die der Differenz entsprechende Anzahl von Unbekannten frei gewählt werden, die übrigen sind dann durch diese Wahl festgelegt. Für die Anzahl der Gleichungen gilt Folgendes:
Das als Beispiel betrachtete Gleichungssystem
besteht aus zwei Gleichungen mit zwei Unbekannten, besitzt also eine
eindeutige Lösung (nämlich ).
Diese Lösung löst aber auch alle weiteren Gleichungen, die aus den ersten beiden
durch Multiplikation mit einer Konstanten und/oder durch Addition miteinander
erhalten werden können. Auf diese Weise könnte im Prinzip ein aus beliebig
vielen Gleichungen bestehendes Gleichungssystem angeschrieben werden,
beispielsweise
(Die dritte Gleichung ist das Dreifache der ersten, die vierte ist die Summe
aus der zweiten und der dritten.) Da die hinzugefügten Gleichungen aber keine
unabhängige neue Information enthalten, ändert ihr Hinzufügen nichts an der
Lösung. Ausschlaggebend für die Lösbarkeit des Systems ist also nicht die Anzahl
der vorliegenden Gleichungen, sondern die kleinste Anzahl von
Gleichungen, auf die sich das Gleichungssystem ohne Informationsverlust
reduzieren lässt. Es existieren mathematische Verfahren zur Ermittlung dieser
Anzahl. Diese Anzahl ist die Anzahl der unabhängigen Gleichungen und
damit diejenige Kennzahl, die die Lösungseigenschaften bestimmt. Welche
der möglichen Gleichungen als minimales Gleichungssystem ausgewählt werden,
spielt für das Lösungsverhalten keine Rolle. Im obigen Beispiel könnten auch die
dritte und die vierte Gleichung als Repräsentanten des Gleichungssystems mit der
unveränderten Lösung
ausgewählt werden:
Anzahl der unabhängigen Reaktionen
Ähnliche Überlegungen gelten für die Anzahl der unabhängigen Reaktionen und die Anzahl der unabhängigen Substanzen, wenn im betrachteten System chemische Reaktionen ablaufen können.
Man betrachte als Beispiel ein geschlossenes System, das im
Gleichgewichtszustand die fünf Substanzen
und
enthält.
Die Reaktionsketten, die im Gleichgewicht zwischen solchen Substanzen auftreten,
können eventuell sehr komplex sein. Unter Umständen führen mehrere
Reaktionspfade gleichzeitig von einer Ausgangssubstanz zum selben
Reaktionsprodukt. Für die Frage, um welche Anzahl die Freiheitsgrade des Systems
durch diese Reaktionen (Gleichgewichtsbedingungen) reduziert werden, dürfen die
alternativen Reaktionspfade nicht mitgezählt werden, ähnlich wie im obigen
Beispiel die abhängigen Gleichungen im Gleichungssystem für die Untersuchung der
Lösbarkeit nicht mitgezählt werden durften.
Da die Anzahl der Atome der einzelnen Elemente konstant bleibt, kann für jede
Atomsorte eine Bilanzgleichung aufgestellt werden (es ist nicht nötig, alle
denkbaren Reaktionsgleichungen zwischen den vorhandenen Stoffen aufzulisten).
Die Analyse dieses Gleichungssystems, im Beispiel je eine Gleichung für ,
und
,
erlaubt ähnlich wie im obigen Beispiel eine Aussage über die Anzahl der
unabhängigen Reaktionen, um die die Anzahl der Freiheitsgrade des Systems
vermindert wird. Im vorliegenden Beispiel ergibt die Analyse, dass nur zwei
unabhängige Reaktionen vorliegen.
Alle anderen im System ablaufenden Reaktionen sind abhängig, lassen sich also
rechnerisch durch Kombination der unabhängigen Reaktionen darstellen und tragen
nicht zur Reduktion der Freiheitsgrade bei.
Anzahl der unabhängigen Substanzen
Die „Anzahl der unabhängigen Substanzen“ ist wie oben erwähnt die Anzahl der
vorhandenen Substanzen (im Beispiel 5) abzüglich der Anzahl der unabhängigen
Reaktionen (im Beispiel 2), im vorliegenden Beispiel also .
Wie sich zeigen lässt, ist sie gleich der so genannten „Anzahl der Komponenten“,
nämlich der minimalen Anzahl der Ausgangsstoffe, die eingesetzt werden müssen,
damit die ablaufenden chemischen Reaktionen im System nach Erreichen des
Gleichgewichtszustands die eingangs beschriebene Zusammensetzung erzeugen
können.
Im vorliegenden Beispiel müssen also mindestens 3 Ausgangssubstanzen eingesetzt
werden. Welche dafür ausgewählt werden, ist für die Phasenregel
unerheblich, eine mögliche Wahl wären etwa
,
und
.
Extensive Variablen
.de.svg.png)
Die Phasenregel beschreibt die Anzahl der Freiheitsgrade des intensiven Zustands des Systems, also die Anzahl der intensiven Zustandsvariablen, die gleichzeitig unabhängig voneinander verändert werden können, ohne dass die Anzahl der koexistierenden Phasen sich ändert. Die Phasenregel macht keine Aussage über die Variierbarkeit der extensiven Variablen.
Wenn beispielsweise Wasser im Tripelpunktszustand vorliegt, können Druck und Temperatur (die beiden intensiven Variablen) nicht geändert werden, ohne dass das System den Tripelpunkt verlässt. Das Volumen des Systems (als extensive Variable) kann dagegen durch Hinzufügen von weiterem Wasser (mit Tripelpunktsdruck und -temperatur) beliebig vergrößert werden, ohne dass das System den intensiven Tripelpunktszustand verlässt. In dem oben im Artikel gezeigten zweidimensionalen p-T-Diagramm ist daher der Tripelpunktszustand als Punkt dargestellt, während er im nebenstehenden Diagramm, in dem die extensive Variable Volumen hinzugenommen wurde, als zur Volumenachse parallele Linie dargestellt ist. Alle Zustände auf dieser Linie haben denselben Druck und dieselbe Temperatur, aber verschiedene Volumina.
Auch die Größenverhältnisse der koexistierenden Phasen untereinander können sich ändern, ohne den intensiven Tripelpunktszustand zu verlassen. In einer Tripelpunktszelle wird der unvermeidliche Zu- oder Abstrom von Wärme durch entsprechenden Latentwärmeumsatz kompensiert, indem sich das Mengenverhältnis der Phasen durch Schmelz-, Gefrier-, Verdunstungs-, Kondensations- oder Sublimationsvorgänge entsprechend verschiebt. Druck und Temperatur bleiben konstant, bis eine der Phasen aufgezehrt ist.
Ob und in welchem Umfang die Variierbarkeit der extensiven Variablen eingeschränkt ist, wird durch die Systemeigenschaften und die Prozessbedingungen bestimmt. Ein System beispielsweise, das in einem starren Behälter eingeschlossen ist, kann nur isochore Prozesse ausführen, bei denen das Systemvolumen konstant bleibt.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 13.11. 2023