Reflexion (Physik)

Reflexion (lateinisch reflexio ‚Zurückbeugung‘, vom Verb reflectere ‚zurückbeugen‘, ‚zurückdrehen‘) bezeichnet in der Physik das Zurückwerfen von Wellen an einer Grenzfläche, an der sich der Wellenwiderstand oder der Brechungsindex des Ausbreitungsmediums ändert.
Bei glatten (also gegenüber der Wellenlänge kleinen Rauigkeitsstrukturen) Oberflächen gilt das Reflexionsgesetz, es liegt der Fall der gerichteten Reflexion vor. An rauen Oberflächen werden Wellen oder (je nach Betrachtungsweise) Strahlung diffus gestreut und in diesem Fall gilt näherungsweise das lambertsche Strahlungsgesetz.
In der Regel wird bei der Reflexion nur ein Teil der Energie der einfallenden Welle reflektiert, man spricht in diesem Zusammenhang auch von partieller Reflexion (teilweiser Reflexion). Der restliche Anteil der Welle breitet sich im zweiten Medium weiter aus (= Transmission), durch den geänderten Wellenwiderstand erfährt die Welle dabei eine Richtungs- (vgl. Brechung) und Geschwindigkeitsänderung. Der Brechungswinkel lässt sich mit dem snelliusschem Brechungsgesetz und die Amplituden der Reflexion und Transmission mit den fresnelschen Formeln berechnen – abhängig von Wellenwiderstand und Polarisation.
Ein Spezialfall der Reflexion ist die Totalreflexion, bei der die Welle beim Einfall auf ein Medium mit niedrigerem Wellenwiderstand vollständig an der Grenzfläche reflektiert wird. Genau betrachtet tritt dies nur bei ideal transparenten Medien auf. Ist beispielsweise das zweite Medium in einem bestimmten Frequenzbereich absorbierend, kommt es zur sogenannten abgeschwächten Totalreflexion, bei der sich das Reflexionsverhalten in diesem Bereich ändert. Angewendet wird die Totalreflexion beispielsweise bei der Retroreflexion (Reflexion einer Welle in Richtung der Quelle).
Eindimensionaler Spezialfall
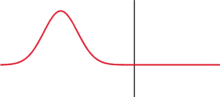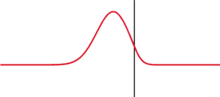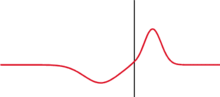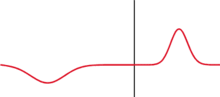
Wenn der Wellenträger die Ausbreitung der Welle nur in einer Raumrichtung zulässt, spricht man von einer eindimensionalen Welle. Beispiele wären Seilwellen, Schallwellen in engen Röhren, elektromagnetische Wellen in Wellenleitern usw. Am Ende eines solchen Wellenträgers kommt es zur Reflexion. Die einlaufende Welle und die gegenläufige reflektierte Welle überlagern sich. Setzt man idealisierend voraus, dass es zu keinem Energieverlust kommt (keine Dämpfung, vollständige Reflexion), so sind die Amplituden der einlaufenden und der auslaufenden Welle gleich. Es bilden sich stehende Wellen aus. Dabei unterscheidet man die Reflexion „am festen Ende“ und „am losen Ende“:
- Am festen Ende ist die Auslenkung der Welle zu jedem Zeitpunkt gleich Null. Die einlaufende und die reflektierte Welle weisen also hier einen Phasenunterschied von π auf, d.h., sie sind gegenphasig und interferieren destruktiv. Am festen Ende entsteht dadurch ein Knoten. Weitere Schwingungsknoten befinden sich jeweils im Abstand halber Wellenlängen. Die Schwingungsbäuche liegen jeweils dazwischen.
- Am losen Ende ist die Auslenkung der Welle maximal. Die einlaufende und die reflektierte Welle weisen keinen Phasenunterschied auf, d.h., sie sind gleichphasig und interferieren konstruktiv. Am losen Ende entsteht dadurch ein Bauch. Weitere Schwingungsbäuche befinden sich im Abstand halber Wellenlänge. Die Schwingungsknoten liegen jeweils dazwischen.
Ob ein Ende fest oder lose ist, hängt davon ab, welche Amplitudengröße man für die Beschreibung der Welle nutzt. So stellt z.B. ein offenes Rohrende für eine Schallwelle ein festes Ende dar, wenn man über den Schalldruck spricht, während sie ein loses Ende für die Schallschnelle ist. Schallschnelle und Schalldruck sind dabei um π/2 phasenverschoben. Findet Reflexion an beiden Enden des Wellenträgers statt, so kann es nur dann zu zeitlich unveränderlichen stehenden Wellen kommen, wenn eine Resonanzbedingung erfüllt ist:
- Hat der Wellenträger zwei feste oder zwei lose Enden, so tritt Resonanz
auf, wenn die Länge des Wellenträgers
ein ganzzahliges Vielfaches der halben Wellenlänge ist:
- Ist das eine Ende des Wellenträgers fest und das andere lose, so lautet
die Resonanzbedingung:
Die auf diese Weise erzeugten stehenden Wellen nutzt man bei vielen Musikinstrumenten aus.
So ist beispielsweise eine Gitarrensaite ein eindimensionaler Wellenträger mit
zwei festen Enden. Zupft man sie an, so schwingt die Saite in den Frequenzen,
die die Resonanzbedingung erfüllen. Für
erhält man die Frequenz des Grundtons. Alle anderen Frequenzen ergeben das Obertonspektrum.
Reflexion einzelner Impulse
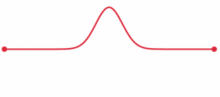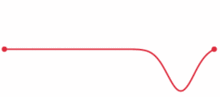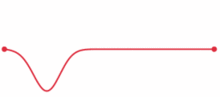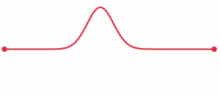
Ein Impuls beliebiger Kurvenform ist ein Wellenpaket, das nach den Regeln der Fourieranalyse in eine Summe von Sinusschwingungen unterschiedlicher Wellenlänge λ zerlegt werden kann. Zwischen zwei Reflektoren im Abstand A sind nur solche erlaubt, für die gilt:
wobei n eine natürliche Zahl ist. Unter bestimmten Voraussetzungen bleibt die Kurvenform des daraus zusammengesetzten Impulses gleich und dieses Soliton kann ungedämpft zwischen den beiden Reflektoren pendeln, wie im Bild zu sehen ist. Durch Vergleich dieser Pendeldauer mit den exakten Zeitmarken einer Atomuhr kann man extrem hohe Frequenzen bestimmen (Frequenzkamm).
Reflexionsgesetz
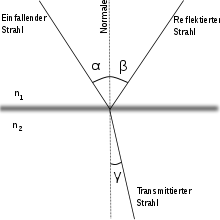
Das Reflexionsgesetz besagt, dass der Ausfallswinkel (auch Reflexionswinkel)
genau so groß wie der Einfallswinkel ist, ,
und beide mit dem Lot in einer Ebene, der Einfallsebene,
liegen. Im Fall von Wellen muss dabei die Wellenlänge erheblich größer sein als
die Abstände zwischen den Streuzentren (beispielsweise Atome). Andernfalls kann
es zur Ausbildung mehrerer „Reflexionsstrahlen“ kommen,
beispielsweise bei Röntgenstrahlen, die an einem Kristall reflektiert werden
(siehe Röntgenbeugung).
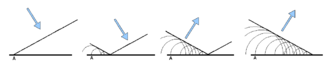
Das Reflexionsgesetz kann mithilfe des huygensschen Prinzips hergeleitet werden (vgl. nebenstehende Abbildung): Im ersten und zweiten Bild sieht man, wie eine Wellenfront schräg auf eine spiegelnde Oberfläche trifft und dabei kreisförmige Elementarwellen um die jeweiligen Auftreffpunkte erzeugt. Die Radien dieser Wellen wachsen mit der Phasengeschwindigkeit der Welle im betreffenden Medium an. In den folgenden Bildern ist dargestellt, wie sich die entstandenen Elementarwellen zu einer neuen Wellenfront überlagern, die nach rechts oben läuft. Die Winkel zwischen den einlaufenden und auslaufenden Wellenfronten und Ebene sind (spiegelverkehrt) gleich. Dies besagt das Reflexionsgesetz.
Eine andere Herleitung macht sich das fermatsche Prinzip zunutze: Der Lichtweg vom Punkt A zum Punkt B ist dann extremal (genauer gesagt: minimal), wenn die Reflexion genau so erfolgt, dass Einfalls- und Ausfallswinkel gleich groß sind.
Gerichtete Reflexion

Das Wellenfeld an einer gerichtet reflektierenden Fläche lässt sich durch „Spiegelquellen“ beschreiben. Zu jeder Originalquelle wird hierbei eine Spiegelquelle hinter der reflektierenden Fläche „angebracht“, mit dem gleichen Abstand zur reflektierenden Fläche wie die Originalquelle. Das Wellenfeld ergibt sich durch Überlagerung der Wellenfelder von Original- und Spiegelquellen.
Anwendungen findet die gerichtete Reflexion in ebenen und nicht ebenen Spiegeln, beispielsweise konkav gekrümmte Hohlspiegel als Rasierspiegel oder bei Spiegelteleskopen. Konvex gekrümmte Spiegel werden als Außenspiegel an Kraftfahrzeugen eingesetzt.
Diffuse Reflexion
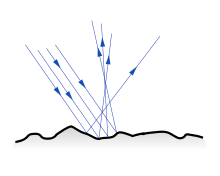
Grenzflächen mit einer großen Rauheit relativ zur Wellenlänge reflektieren diffus. Enthält das Material viele Streuzentren, folgt die Reflexion dem lambertschen Gesetz. Die Hauptrückstreuung erfolgt dann senkrecht zum Material, unabhängig von der Einstrahlungsrichtung. Beispiele sind Milch, Wandfarbe oder Papier. Bei Milch haben die Fetttropfen im Wasser die Größenordnung der Wellenlänge des sichtbaren Lichtes und bilden die Streuzentren für Lichtwellen, gleiches gilt für die Lufteinschlüsse zwischen den Fasern bei Papier.
Anwendungen diffuser Reflexion, also der gleichmäßigen Verteilung von Licht, sind
- Ulbricht-Kugel,
- Projektionsschirm,
- Vermeidung spiegelnder Reflexe an Bildschirmen und fotografischen Abzügen.
Die Summe spiegelnder und diffuser Reflexion wird auch Remission genannt, bezogen auf die eingestrahlte Lichtmenge Remissionsgrad. Für nicht perfekt diffus streuende, gekrümmte und womöglich farbstichige Oberflächen gibt es unterschiedliche Möglichkeiten der Definition. In der Meteorologie gibt die Albedo den Anteil des Sonnenlichts an, der von der Erdoberfläche, oder von Wolken diffus reflektiert wird. Die Albedo von anderen nicht selbst leuchtenden Himmelskörpern geht in der Astronomie in die Helligkeit ein, mit der dieser Himmelskörper von der Erde aus zu sehen ist.
In der Industrie sind verschiedene Definitionen des Weißgrads üblich. Einige Definitionen berücksichtigen unter anderem, dass das menschliche Auge für manche Wellenlängen empfindlicher ist als für andere.
Reflexion elektromagnetischer Wellen in der Optik
.png)
.svg.png)
Im Folgenden soll die Reflexion am Beispiel elektromagnetischer Wellen erklärt werden. Zum einfacheren Verständnis wird dabei das Strahlmodell der geometrischen Optik genutzt.
In der Schemazeichnung (siehe Reflexionsgesetz) trifft ein Strahl von links oben auf die Oberfläche eines Mediums mit anderen Strahlungsausbreitungseigenschaften. Ein Teil der Strahlung wird zum Lot hin gebrochen (transmittierter Teil), ein anderer reflektiert. Dabei gilt das Reflexionsgesetz: Der Einfallswinkel ist gleich dem Reflexionswinkel. Unter geeigneten Bedingungen kann jedoch die einfallende Strahlung vollständig reflektiert werden, wie bei Totalreflexion.
Die Reflexion von elektromagnetischer Strahlung an einer Grenzfläche erfolgt in der Regel nur teilweise, der andere Teil wird transmittiert. Der Reflexionsgrad ist definiert als das Verhältnis der reflektierten zur einfallenden Lichtintensität
Der Reflexionsgrad kann über den Reflexionsfaktor aus den fresnelschen Formeln berechnet werden. Er ist vom Einfallswinkel und Polarisation des Lichts sowie von den Eigenschaften der beteiligten Materialien abhängig. Bei zirkular polarisierten Wellen ändert sich bei jeder Reflexion die Helizität.
Der Brechungsindex ist im Allgemeinen abhängig von der Wellenlänge. Das heißt, Wellen unterschiedlicher Wellenlänge können unterschiedlich stark reflektiert werden. Beispielsweise besitzen Metalle aufgrund der Absorption durch das Elektronengas einen hohen Extinktionskoeffizienten für elektromagnetische Strahlung im Infrarot-Bereich, sie sind damit undurchsichtig und weisen einen sehr hohen Reflexionsgrad von im Allgemeinen mehr als 90 Prozent auf. Hingegen sinkt der Reflexionsgrad von Metallen im sichtbaren oder ultravioletten Bereich mitunter innerhalb eines kleinen Frequenzbereichs sehr schnell (siehe Bild mit dem Beispiel Silber). In der Reflexionsspektroskopie schließt man vom gemessenen Reflexionsspektrum auf im Material wirksame Mechanismen und deren Parameter wie die Dichte der Elektronen im Leitungsband, oder Polarisierbarkeiten.
Durch den unterschiedlichen Reflexionsgrad in Abhängigkeit vom Einfallswinkel
und von der Polarisation des Lichts ändert sich diese bei jeder schrägen
Reflexion. Das heißt, fällt unpolarisiertes Licht auf eine schräge Grenzfläche,
so ist das reflektierte und das gebrochene Licht (bei
und
)
teilweise polarisiert. In dem Sonderfall
wird der parallel zur Einfallsebene polarisierte Lichtanteil überhaupt nicht
reflektiert, sondern vollständig gebrochen (Brewster-Winkel).
Der reflektierte Anteil ist danach vollständig senkrecht polarisiert und der
transmittierte enthält beide Polarisationsrichtungen. Dieser Effekt ermöglicht
es zum Beispiel, Laserstrahlung ohne
Reflexionsverlust durch ein Brewsterfenster
aus der Kavität austreten zu lassen.
Weiteren Einfluss auf die Reflexion hat der von der Kristallorientierung abhängige Indexellipsoid von doppelbrechenden Materialien. Hier unterscheidet sich der Reflexionsgrad zusätzlich abhängig von der Kristallorientierung der Kristalloberfläche. Auch ein Magnetfeld kann die Reflexion beeinflussen, was technisch bei magnetooptischen Speichermedien ausgenutzt wird.
Eine Verringerung oder Erhöhung der Reflexion kann durch Interferenz an einer oder mehreren dielektrischen Schichten erreicht werden und wird zur Antireflexbeschichtung oder zur Herstellung dichroitischer Spiegel genutzt.
Anwendung
Ein wesentlicher Anwendungsbereich der Reflexion von elektromagnetischen Wellen bzw. Strahlen ist deren gezielte Führung. Ausgenutzt wird das u.a. beim Spiegel, der zum Beispiel das von einer Person gestreute Licht gerichtet zurückwirft, sodass die Person sich selbst sehen kann. Technisch wird die Reflexion an ebenen Spiegeln oder Prismen zur Strahlumlenkung angewendet, beispielsweise in Periskopen oder im Umlenkprisma bzw. dem Klappspiegel von Spiegelreflexkameras.
Reflexion lässt sich auch zur berührungslosen Erfassung bzw. Vermessung spiegelnder Oberflächen (Deflektometrie) oder zur Messung des Abstands einer Strahlungsquelle zu einer reflektierenden Oberfläche nutzen (Laufzeitmessung oder Interferometrie). Beispiele sind Laser-Entfernungsmesser, Reflexlichtschranken oder die Zeitbereichsreflektometrie
Des Weiteren wird die Reflexion an Hohlspiegeln benutzt, um elektromagnetische Strahlen zu bündeln. Mit Parabolantennen wird eine Richtwirkung erreicht. Beispiele für optische Wellenlängen sind Scheinwerfer oder Spiegelteleskope.

Die Art und Weise, wie ein Körper aufgrund von Material, Form und Oberflächenbeschaffenheit Licht reflektiert, wird auch in vielen gestalterischen Bereichen wie dem Produktdesign oder der Architektur eingesetzt. So werden beispielsweise Oberflächen poliert, um einen glänzenden, spiegelnden Eindruck zu erzeugen, oder aufgeraut/geschliffen, um diffus zu reflektieren. Ähnliche Wirkung kann auch mit der Verwendung unterschiedlicher Lacke (z.B. glänzend, seidenmatt, matt) erzeugt werden.
Die Art der Reflexion kann Einfluss auf technische Parameter haben, so wird bei matten Bildschirmen der störende Einfluss von Streulichtreflexionen mithilfe der diffusen Reflexion an einer rauen Oberfläche reduziert. Die raue Oberfläche vermindert im Vergleich zu spiegelnden Displays jedoch auch den Schwarzeindruck und die Farbbrillanz des durch die Schutzscheibe transmittierten Lichts.
Da bei der Reflexion ein für ein Material charakteristischer Intensitätsanteil reflektiert wird, können auf diese Weise auch Eigenschaften von Materialien, wie Brechungsindex, Dicke, Verunreinigungen usw., bestimmt werden. Hierbei werden sowohl Messungen bei einer einzigen Wellenlänge also auch spektrale Verteilungen genutzt (reflektometrische Dünnschichtmessung, Ellipsometrie). Letztere bilden die Grundlage für die Spektroskopie, bei der, neben der Transmission, die Reflexion von polarisierten als auch unpolarisierten elektromagnetischen Wellen eine häufig genutzte Untersuchungstechnik darstellt.
Reflexion bei elektrischen Leitungen
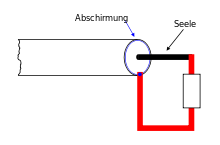
Wenn eine elektrische Welle mit der Amplitude A0 durch eine
Leitung geführt wird,
die mit ihrem Wellenwiderstand
abgeschlossen ist, wird sie dort vollständig, ohne Reflexion und unabhängig von
ihrer Frequenz absorbiert. Der Abschluss kann ein Lastwiderstand sein, eine
Antenne, der Eingangswiderstand einer analogen oder digitalen Schaltung oder
auch eine oder mehrere weitere Leitungen. Bei Fehlanpassung
kommt es – Linearität vorausgesetzt – zu einer reflektierten Welle gleicher
Frequenz und (meist) geänderter Amplitude AR. Das Verhältnis
AR/A0 bezeichnet man als Reflexionsfaktor
:
Darin sind
die Impedanz des Abschlusses und
der Wellenwiderstand der Leitung.
Im Allgemeinen ist
frequenzabhängig und komplex,
typischerweise mit Betrag kleiner als 1; sein Argument
bedeutet eine Phasenänderung. In der Praxis wird stets ein reeller Wert
angestrebt.
Spezialfälle:
bedeutet, dass die Welle nicht reflektiert wird, es gibt also kein Echo. (Fall: angepasste Leitung).
bedeutet, dass die Welle vollständig reflektiert wird (offenes Ende = Spannungsverdopplung durch Überlagerung der vorlaufenden und reflektierten Welle).
bedeutet, dass die Welle voll reflektiert, dabei aber invertiert wird (Kurzgeschlossenes Ende; Spannung = 0 durch Überlagerung der vorlaufenden und reflektierten Welle).
Eine Anwendung wird im Artikel Zeitbereichsreflektometrie beschrieben. Die auf der Leitung laufenden vorlaufenden und reflektierten Wellen können sich überlagern und zu einer ortsabhängigen Verteilung von Strom und Spannung führen (stehende Wellen).
Reflexion von Spannungssprüngen
Schlägt ein Blitz in eine Hochspannungsleitung ein, läuft ein Hochspannungsimpuls bis zum Ende der Leitung und kann dort Zerstörungen hervorrufen. Ähnliches beobachtet man in Kabeln und Leitungen (Flachbandleitung, Koaxialkabel mit Leitungsimpedanz Z), wenn ein Spannungssprung eingespeist wird – zum Beispiel, indem der Kabelanfang an eine Gleichspannung geschaltet wird. Die Gleichspannung werde von einer Stromversorgung mit dem Innenwiderstand R=Z geliefert, sodass ein reflexionsfreier Einlauf des Spannungssprungs in das Kabel stattfindet.
Unendlich langes Kabel
Wird die Gleichspannung U zum Zeitpunkt Null an ein unendlich langes verlustfreies Kabel gelegt, würde ewig ein konstanter Strom I fließen:
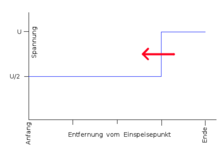
Am Einspeisepunkt tritt unabhängig davon, ob und wie das Kabelende beschaltet ist, eine konstante Spannung U/2 auf. Man kann am Einspeisepunkt nicht unterscheiden, was am Kabelende ist. Das Kabel speichert die elektrische Energie und nach unendlich langer Zeit ist das Kabel „geladen“ (Magnetfeld, elektrisches Feld).
Man kann den Zeitpunkt der Ankunft des Spannungssprungs an einem entfernten
Messpunkt vorhersagen, denn die Ausbreitungsgeschwindigkeit des Sprunges ist
cmedium. Das Isolationsmaterial mit der relativen Permittivität
zwischen den Leitern des Kabels bestimmt die Impulsgeschwindigkeit
im Kabel
Endliche Kabellänge
Hat das Kabel im obigen Gedankenversuch die endliche Länge L, kommt der Spannungssprung nach der Zeit
am Kabelende an. Der dortige Abschluss entscheidet, wie es weitergeht:
Reflexionsfreier Abschluss
Sind Innen- und Außenleiter des Koaxialkabels über einen Widerstand R = Z verbunden, fließt die elektrische Energie reflexionsfrei in diesen Abschlusswiderstand, der sich entsprechend erwärmt. Am Einspeisepunkt (Kabelanfang) kann man diesen Fall nicht von einem unendlich langen Kabel unterscheiden.
Offenes Ende
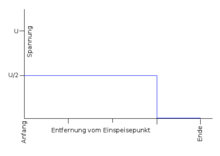
Sind Innen- und Außenleiter nicht verbunden, wird der Spannungssprung phasengleich reflektiert. Das führt zu einer Verdopplung der Spannung und der überlagerte Spannungssprung läuft mit cmedium zurück zum Kabelanfang (siehe Bild rechts oben). Zurück am Einspeisepunkt, wird er dort nicht reflektiert, weil der Innenwiderstand der Stromversorgung der Leitungsimpedanz entspricht (reflexionsfreier Abschluss). Sobald der Spannungssprung am Einspeisepunkt eintrifft, ist der Gleichgewichtszustand erreicht, es fließt kein weiterer Strom und an jedem Punkt des Kabels misst man zwischen den Leitern die Spannung U. Mit einem Speicheroszilloskop lässt sich diese „Spannungstreppe“ auf zunächst U/2 und dann – ab dem Zeitpunkt 2T – auf U aufzeichnen.
Kurzgeschlossenes Ende
Sind die Leiter am Ende kurzgeschlossen, wird der Spannungssprung gegenphasig reflektiert. Die vor- und rücklaufende Welle überlagert sich zu Null. Das misst man am Kabelanfang aber erst dann, wenn der reflektierte Spannungssprung nach der Zeit 2·T dort ankommt. Mit einem Oszilloskop lässt sich dieser rechteckige Impuls (Null auf U/2 beim Einschalten und nach der Zeit 2T auf Null) aufzeichnen. Ein am Ende kurzgeschlossenes Kabel wirkt also wie ein „verzögerter Kurzschluss“.
Anwendung
Kabel mit definierter Länge, die am Ende kurzgeschlossen, angepasst oder offen sind, werden als Zeitglied (Laufzeit), zur Impulsverzögerung oder -speicherung, als Leitungskreis (Schwingkreis, Sperrkreis, Filter, Impedanztransformation, Phasendrehung) oder mit veränderlicher Länge zum Messen der Wellenlänge bzw. Frequenz eingesetzt.
Siehe auch Lecherleitung.
Reflexion in der Akustik
Typen von Reflexionen
In der Akustik ist die Schallreflexion gemeint, also der Rückwurf von Schall. Ebene, schallharte, nicht absorbierende Oberflächen reflektieren gut die Schallwellen. Beim Erkennen dieser Schallreflexionen spielt die Echowahrnehmungsschwelle eine bedeutende Rolle. Je nach Anordnung und Anzahl der reflektierenden Flächen und Art der Beschallung ergibt sich ein unterschiedlicher Höreindruck:
- Echos (Felswand in größerem Abstand)
- Flatterecho (zwei parallele reflektierende Wände)
- Nachhall (große Räume mit harten Wänden, wie in Kirchen)
- hohe Räumlichkeit (akustisches Raumempfinden in Konzertsälen)
- trockener Klang (in Räumen mit wenig reflektierenden Flächen)
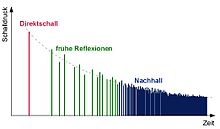
Für den akustischen Eindruck wichtig sind:
- Anteil des Direktschalls am Gesamtschallpegel
- Zeitverzögerung und Richtung von frühen Reflexionen, sowie deren Anteil am Gesamtschallpegel
- Einsatzverzögerung und räumliche Verteilung des Nachhalls, sowie dessen Anteil am Gesamtschallpegel und dessen zeitlicher Verlauf (Nachhallzeit)
Raumakustisches Design
Bei Räumen sind je nach Nutzung andere raumakustische Eigenschaften und damit jeweils ein anderes Reflexionsverhalten der Wände sinnvoll:
- Bis zu einer gewissen Grenze reflexionsarme Räume bei Tonstudios (also keine schalltoten Räume), damit der akustische Charakter des Aufnahmeraums möglichst geringen Einfluss auf die Aufnahme bekommt.
- Räume mit mäßig reflektierenden Wänden für Unterrichtsräume. Einerseits soll die Stimme des Lehrers durch frühe Reflexionen bis 15 ms unterstützt werden, andererseits darf die Sprachverständlichkeit aber nicht durch zu starke späte Reflexionen und zu hohe Nachhallzeit vermindert werden. Die günstige Nachhallzeit für Normalhörende nach DIN 18041 „Hörsamkeit in kleinen bis mittelgroßen Räumen“ liegt abhängig vom Raumvolumen zwischen 0,3 und 0,8 Sekunden. In Klassenzimmer mit einem Volumen von 125 bis 250 m³ ist eine Nachhallzeit von 0,4 bis 0,6 Sekunden optimal. Für Hörbehinderte sollten Nachhallzeiten um 0,3 Sekunden angestrebt werden.
- Räume mit stark reflektierenden Wänden und einem ausgewogenen Verhältnis von Direktschall, frühen Reflexionen und Nachhall für Konzertsäle. Hier ist es das Ziel, durch frühe Wandreflexionen die seitlich auf die Ohren einfallen ein möglichst „räumliches“ Musikerlebnis zu erzielen. Auch eine hohe Diffusität, also Streuung des Schalls ist wichtig. Günstige Nachhallzeit liegt bei 1,5 bis 2 Sekunden.
Eine ganz besondere Bedeutung bei der räumlichen Raumerkennung hat die Anfangszeitlücke (ITDG).
Zusammenhang Reflexion, Absorption, Transmission
Folgende Größen spielen bei Schallreflexionen eine Rolle:
- Der Schallreflexionsgrad
oder
ist ein Maß für die reflektierte Schallintensität.
- Der Schallabsorptionsgrad
oder
ist ein Maß für die absorbierte Schallintensität.
- Der Schalltransmissionsgrad
oder
ist ein Maß für die durchgelassene Schallintensität.
- Der Schalldissipationsgrad
oder
ist ein Maß für die „verlorengegangene“ Schallintensität.
Bei Auftreffen auf Begrenzungsflächen wird die eintreffende Schallintensität entweder an der Begrenzungsfläche reflektiert oder von der Begrenzungsfläche absorbiert. Es gilt somit
Der absorbierte Anteil der Schallintensität wird hierbei entweder von der Begrenzungsfläche durchgelassen (transmittiert) oder in den Materialien der Begrenzungsfläche in Wärme umgewandelt (dissipiert). Es gilt somit
Somit gilt insgesamt
In der Akustik gehören folgende Wörter zur gestörten Schallausbreitung
Reflexion von Wasserwellen
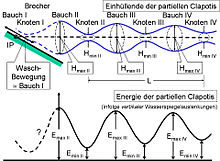
Wellenreflexion bedeutet bei fortschreitenden Wasserwellen das Zurückwerfen eines Teils ihrer Energie an einem Bauwerk (Wellenbrecher, Uferböschung) oder an Orten, wo sich die Konfiguration des natürlichen Meeresgrundes (stark) ändert. Zugleich wird ein anderer Anteil der Wellenenergie fortgeleitet und der restliche Anteil durch die Prozesse des Wellenbrechens, der Flüssigkeits- und Bodenreibung dissipiert und absorbiert, vergleiche dazu Wellentransformation, Wellenabsorption.
Dementsprechend lautet das Gesetz von der Erhaltung der Energie:
Darin bedeuten
= Energie der anlaufenden Wellen
= Energie der (durch das Bauwerk) fortgeleiteten (transmittierten) Wellen
= Energie der am Bauwerk reflektierten Wellen
= Energieverlust infolge der Wellenabsorption.
Werden die genannten Energieanteile ,
,
jeweils in das Verhältnis zur Energie der anlaufenden Wellen
gesetzt, können solche Werte als Transmissionskoeffizient,
Reflexionskoeffizient
und Absorptionskoeffizient
angegeben werden. Im Allgemeinen ist der Reflexionskoeffizient
.
Nur im theoretischen Fall der perfekten Reflexion (bei Vorliegen einer
perfekten Clapotis) ist
.
Nur hierfür gilt auch die Aussage, dass bei der Reflexion an einer ideal glatten
vertikalen Wand ein Phasensprung
nicht auftritt. Insbesondere bei partieller Reflexion an steilen, ebenen
Uferböschungen kann der Phasensprung etwa 180° betragen, vergl. nebenstehendes
Bild.
Da die Wellenenergie dem
Wellenhöhenquadrat proportional ist, kann der Reflexionskoeffizient auch
einfacher als Quotient der Höhe der reflektierten Welle
und der Höhe der anlaufenden Welle
geschrieben werden
.
Reflexion durch ein anziehendes Potential
In der klassischen Mechanik kann in einer Dimension eine Reflexion nur an einem abstoßenden Potential erfolgen. Im Rahmen der Quantenmechanik ist jedoch auch eine Reflexion an einem anziehenden Potential möglich. Dieser der Anschauung widersprechende Vorgang wird Quantenreflexion genannt.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 10.06. 2024