Plasmahalbwertszeit

Als Plasmahalbwertszeit, fallweise auch als Eliminationshalbwertszeit bezeichnet, definiert man diejenige Zeitspanne, die nach intravenöser Verabreichung zwischen der Maximalkonzentration eines Arzneistoffes im Blutplasma bis zum Abfall auf die Hälfte dieses Wertes verstreicht. Dieser Parameter stellt eine wichtige Kenngröße in der Pharmakokinetik dar und wird häufig mit dem Symbol $t_{1/2}$ angegeben.

Die Plasmahalbwertszeit ist abhängig von zahlreichen Einflussgrößen auf das zirkulierende Vollblut im Organismus. Arzneistoffe können unter anderem in der Leber metabolisiert werden, sich in Geweben anreichern, von der Niere ausgeschieden werden oder die Blut-Hirn-Schranke überwinden. Wird der Arzneistoff durch die Leber abgebaut, so ergibt sich meist ein exponentieller Ablauf der Arzneistoffkonzentration über die Zeit, der mit folgender Gleichung beschrieben werden kann:

$C(t)=C_{0}e^{-kt}$

mit

$C(t)$ : Konzentration nach der Zeit $t$

$C_{0}$ : Anfangskonzentration ( $t=0$ )

$k$ Eliminationskonstante

Die Beziehung zwischen der Eliminationskonstante und der Halbwertszeit ist durch folgende Gleichung beschrieben:

$k={\frac {\ln 2}{t_{1/2}}}$

mit

$t_{1/2}$ : Zeitraum, in der sich die Konzentration halbiert

Obige Zusammenhänge gelten nur nach intravenöser Verabreichung im Ein-Kompartiment-Modell (d. h., es findet keine Verteilung in „tiefere“ Kompartimente statt). In allen anderen Fällen (etwa auch nach extravasaler Verabreichung) wird die Plasmahalbwertszeit zu möglichst späten Zeiten aus der Konzentrations-Zeit-Kurve bestimmt, um verfälschende Einflüsse der Absorption oder Verteilung gering zu halten.

Terminale Halbwertszeit

Weist eine Substanz eine ausgeprägtes Verteilungverhalten auf, so resultiert ein biphasischer Verlauf im Abfall der Plasmakonzentrations-Zeit-Kurve: initial fällt die Kurve rasch ab, bis ein Verteilungsgleichgewicht erreicht ist, danach flacht der Verlauf ab und wird hauptsächlich durch die Elimination (Metabolisierung und Ausscheidung) bestimmt.^[1] Terminale Halbwertszeit (t_½β) wird der Zeitraum genannt, in dem der Plasmaspiegel in der Eliminationsphase (terminale Phase) auf jeweils die Hälfte absinkt.^[2]

Kontextsensitive Halbwertszeit

Insbesondere in der Anästhesiologie sind im Zusammenhang mit der Infusion von Schmerz- und Narkosemitteln therapeutisch bedeutsame Umverteilungsprozesse zu berücksichtigen, so dass 1992 der Begriff der sogenannten kontextsensitiven Halbwertszeit eingeführt wurde. Sie ist definiert als die Zeit, die notwendig ist, bis die Plasmakonzentration eines Wirkstoffs nach kontinuierlicher Infusion von definierter Dauer („Kontext“) auf die Hälfte abgesunken ist.^[3]


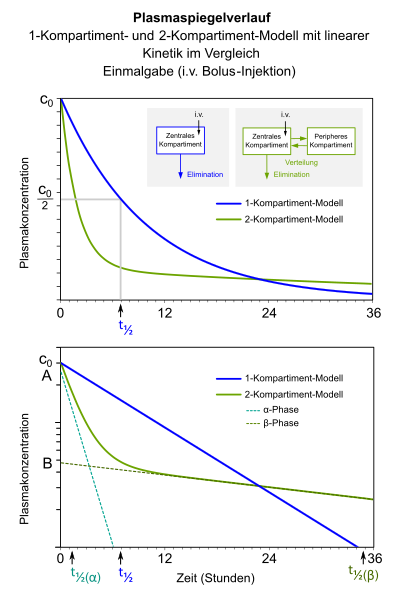
	Simulation von Plasmaspiegelverläufen nach i.v.-Bolus-Injektion eines Wirkstoffes in einem 1-Kompartiment-Modell (blau) und einem 2-Kompartiment-Modell (grün); oben lineare, unten halblogarithmische Darstellung. Im 1-Kompartiment-Modell verläuft die Elimination aus dem zentralen Kompartiment mit der Geschwindigkeitskonstante ${\mathrm {k} _{e}}$ exponentiell abfallend. Die Plasmahalbwertszeit $t_{1/2}$ , also der Zeitraum, in dem die Ausgangskonzentration $C_{0}$ des Wirkstoffes im Plasma auf die Hälfte absinkt, ergibt sich als $t_{1/2}={\frac {\ln 2}{\mathrm {k} _{e}}}$ . Das 2-Kompartiment-Modell berücksichtigt zusätzlich zum Eliminationsvorgang eine Verteilung in ein peripheres Kompartiment. Hier verläuft die Konzentrations-Zeit-Kurve biphasisch: die $\alpha$ -Phase mit dem raschen Abfall ist durch den Verteilungsvorgang geprägt, die ${\beta }$ -Phase zeigt eine langsamere Abnahme, da die Elimination zum Teil durch die Rückverteilung kompensiert wird. Der Konzentrations-Zeit-Verlauf ist durch die zwei Plasmahalbwertszeiten $t_{{1/2}({\alpha })}$ (initiale Halbwertszeit) und $t_{{1/2}({\beta })}$ (terminale Halbwertszeit) charakterisiert. Sie lassen sich aus den Hybridkonstanten $\alpha$ und $\beta$ der Exponentialfunktionen in ${\mathrm {C} _{t}}}=A\cdot {{e}^{{-\alpha }{\mathrm {t} }}}+B\cdot {{e}^{{-\beta }{\mathrm {t} }}$ berechnen. Es gilt $A+B=C_{0}$ .^[4] Die terminale Halbwertszeit ist bedeutsam mit Blick auf die Anreicherung von Wirkstoffen (Akkumulation) im Körper bei längerer Anwendung.

Die Plasmahalbwertszeit ist begrifflich abzugrenzen von der Stabilität eines Arznei- oder biologischen Stoffs im Blutplasma selbst. Für diese Fragestellung wird der Begriff Plasmastabilität verwendet, diese ist beispielsweise bei Lagerung, Transport und Analytik von Plasmaproben,^[5] aber auch für die Entwicklung von Arzneistoffen^[6] von Bedeutung.

Siehe auch

Einzelnachweise

↑ G. Geisslinger et al.: Mutschler Arzneimittelwirkungen. 11. Auflage. WVG, Stuttgart 2019, S. 32 f.
↑ A. Röper, P.M. Lauven: Pharmakologisches Wissen – Pharmakodynamik und Pharmakokinetik. In: Franz-Josef Kretz, Frank Teufel (Hrsg.): Anästhesie und Intensivmedizin. Springer-Verlag, 2006. S. 5.
↑ M. Schäfer, C. Zöllner: Opioide in der Anästhesiologie. In: Rossaint et al. (Hrsg.): Die Anästhesiologie. Springer Reference Medizin. Springer, Berlin, Heidelberg. 2016. S. 1–24.
↑ In Anlehnung an: M. Gibaldi, D. Perrier: Pharmacokinetics. Marcel Dekker, New York, 1975. S. 45 ff.
↑ G. A. Reed: Stability of Drugs, Drug Candidates, and Metabolites in Blood and Plasma. In: Current protocols in pharmacology. Band 75, 12 2016, S. 7.6.1–7.6.12, doi:10.1002/cpph.16, PMID 27960029, PMC 5198715 (freier Volltext).
↑ L. Di, E. H. Kerns, Y. Hong, H. Chen: Development and application of high throughput plasma stability assay for drug discovery. In: International journal of pharmaceutics. Band 297, Nummer 1–2, Juni 2005, S. 110–119, doi:10.1016/j.ijpharm.2005.03.022, PMID 15876500.

Basierend auf einem Artikel in:

Wikipedia.de