Probit

Ein Probit ist in der Statistik die zu einer Wahrscheinlichkeit $p\in (0,1)$ gebildete Größe $\Phi ^{-1}(p)\in \mathbb {R}$ , wobei $\Phi ^{-1}$ die Umkehrfunktion der Verteilungsfunktion $\Phi$ der Standardnormalverteilung bezeichnet. Unter der Probit-Transformation versteht man die Transformation von Wahrscheinlichkeiten in Probits. Diese Transformation wird im Probit-Modell, einem speziellen verallgemeinerten linearen Modell, zur Spezifikation der Kopplungsfunktion verwendet.

Darstellung der Probit-Funktion

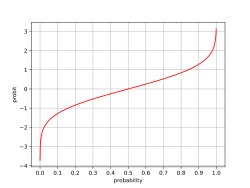
In der Biometrie werden in der sogenannten Probitanalyse zur Untersuchung von Dosis-Wirkung-Beziehungen die Begriffe Probit und Probit-Transformation in einer verwandten, aber abweichenden Bedeutung verwendet.

Definition

Für eine Wahrscheinlichkeit $0<p<1$ heißt

$\operatorname {probit} (p)=\Phi ^{-1}(p)$

Probit von $\Phi$ die Verteilungsfunktion der Standardnormalverteilung bezeichnet. Die Funktion $\operatorname {probit} \colon (0,1)\to \mathbb {R}$ heißt auch Probit-Funktion. Wenn Wahrscheinlichkeiten $p\in (0,1)$ in $\operatorname {probit} (p)\in \mathbb {R}$ transformiert werden, spricht man auch von einer Probit-Transformation.

Eigenschaften

Es gilt

$\operatorname {probit} (p){\begin{cases}<0&{\text{für }}p<1/2\\=0&{\text{für }}p=1/2\\>0&{\text{für }}p>1/2\end{cases}}\;.$

Die Probit-Funktion besitzt die Symmetrieeigenschaft

$\operatorname {probit} (1-p)=-\operatorname {probit} (p)\quad {\text{für alle }}0<p<1$

Die Probit-Funktion ist streng monoton und hat die Grenzwerte

$\lim _{p\to 0}\operatorname {probit} (p)=-\infty \quad {\text{und}}\quad \lim _{p\to 1}\operatorname {probit} (p)=\infty \;.$

Die Probit-Funktion ist differenzierbar und hat die Ableitungsfunktion

$\operatorname {probit} '(p)={\frac {1}{\varphi (\Phi ^{-1}(p))}}>0\quad {\text{für alle }}0<p<1,$

wobei $\varphi$ die Dichtefunktion der Standardnormalverteilung bezeichnet.

Die Probit-Funktion ist invertierbar. Ihre Umkehrfunktion ist die Verteilungsfunktion der Standardnormalverteilung.
Formal ist $\operatorname {probit} (p)$ das $p$ -Quantil der Standardnormalverteilung und die Probit-Funktion ist die Quantilfunktion einer standardnormalverteilten Zufallsvariablen.

Anwendungen

Die Bezeichnung Probit hat sich in bestimmten Anwendungsgebieten der Statistik durchgesetzt, auch als sprachliche Parallele zu Logit.
Mit binären Regressionsmodellen wird die Wahrscheinlichkeitsverteilung einer erklärten binären Variable mit den möglichen Werten 0 und 1 durch eine affin lineare Funktion erklärender Variablen bestimmt. Im Probit-Modell^[1]^[2] wird die Probit-Funktion zur Verbindung der Verteilung der erklärten Variablen mit den erklärenden Variablen verwendet,

$\mathrm {probit} (P(Y_{i}=1))=\beta _{0}+\sum _{j=1}^{p}\beta _{j}x_{ij}\quad i=1,\dots ,n\;.$

Dabei ist $x_{ij}$ der $i$ -te beobachtete Werte der $j$ -ten erklärenden Variablen und $n$ ist die Anzahl der Beobachtungen. Eine häufig verwendete Alternative zum Probit-Modell ist das Logit-Modell, bei dem die Logit-Funktion $\mathrm {logit} (p)=\ln(p/(1-p)$ an die Stelle der Probit-Funktion tritt.

Mit ordinalen Regressionsmodellen wird die Wahrscheinlichkeitsverteilung einer erklärten ordinalen Variable, die eine endliche Anzahl von Kategorien hat, durch eine affin lineare Funktion erklärender Variablen bestimmt. Im ordinalen Probit-Modell werden in der Variante des kumulativen Modells für die erklärte kategoriale Variable mit $K$ Kategorien die Wahrscheinlichkeiten $P(Y_{i}\leq k)$ für $k=1,\dots ,K$ als

$\mathrm {probit} (P(Y_{i}\leq k))=\beta _{0k}+\sum _{j=1}^{p}\beta _{j}x_{ij},\quad i=1,\dots ,n$

modelliert.^[3] Dabei gilt $\beta _{01}\leq \beta _{02}\leq \dots \leq \beta _{0k}$ . Wie im binären Probit-Modell kann anstelle der Probit-Funktion die Logit-Funktion verwendet werden.

Im Bereich der Ökonometrie wird das Probit-Modell gerne verwendet, da es als ein Schwellenwert-Modell mit einem latenten normalverteilten Fehlerterm interpretiert werden kann.^[4] Dagegen wird in biometrischen Anwendungen überwiegend die Logit-Variante des Modells verwendet, da die Logits Logarithmen der Odds (bzw. der kumulativen Odds im Fall des ordinalen Modells) sind, da Odds und Chancenverhältnisse im Bereich der Biometrie eine wichtige Rolle spielen.^[3]

Probitanalyse in der Biometrie

In der Biometrie heißt ein Teilgebiet der Untersuchung von Dosis-Wirkung-Beziehungen Probitanalyse^[5]^[6]. Dort findet sich folgende abweichende Terminologie für den Begriff Probit-Transformation. Für eine Zufallsvariable $X$ , deren dekadischer Logarithmus $\lg X$ einer Normalverteilung mit den Parametern $\mu$ und $\sigma ^{2}$ genügt, ist die Zufallsvariable $(\lg X-\mu )/\sigma$ standardnormalverteilt und die Zufallsvariable $5+(\lg X-\mu )/\sigma$ nimmt mit sehr großer Wahrscheinlichkeit positive Werte an. Die Transformation der Messwerte

$x\mapsto 5+{\frac {\lg x-\mu }{\sigma }}$

heißt in diesem Zusammenhang Probit-Transformation. In diesem Zusammenhang wird der zu einer Wahrscheinlichkeit $p$ gehörende Probit als der Wert $\Phi ^{-1}(p)+5$ definiert.^[7]

Einzelnachweise

↑ Gerhard Tutz: Die Analyse kategorialer Daten – Anwendungsorientierte Einführung in Logit-Modellierung und kategoriale Regression. Oldenbourg, München / Wien 2000, ISBN 3-486-25405-7, 4.2.1 Probit-Modell, S. 122.
↑ Gerhard Tutz: Regression for Categorical Data. Cambridge University Press, Cambridge 2012, ISBN 978-1-107-00965-3, Probit Model, S. 123–124.
↑ ^{Hochspringen nach: a} ^b Gerhard Tutz: Regression for Categorical Data. Cambridge University Press, Cambridge 2012, ISBN 978-1-107-00965-3, Probit Model, S. 248.
↑ Gerhard Tutz: Modelle für kategoriale Daten mit ordinalem Skalenniveau – Parametrische und nonparametrische Ansätze. Vandenhoeck & Ruprecht, Göttingen 1990, ISBN 3-525-11268-8, S. 76–77.
↑ P. H. Müller (Hrsg.): Lexikon der Stochastik – Wahrscheinlichkeitsrechnung und mathematische Statistik. 5. Auflage. Akademie-Verlag, Berlin 1991, ISBN 978-3-05-500608-1, Probitanalyse, S. 307–309.
↑ D. J. Finney: Probit Analysis. 3. Auflage. Cambridge University Press, Cambridge 1971.
↑ P. H. Müller (Hrsg.): Lexikon der Stochastik – Wahrscheinlichkeitsrechnung und mathematische Statistik. 5. Auflage. Akademie-Verlag, Berlin 1991, ISBN 978-3-05-500608-1, Probitanalyse, S. 308.

Basierend auf einem Artikel in:

Wikipedia.de