Periodische Funktion
In der Mathematik sind periodische Funktionen eine besondere Klasse von Funktionen. Sie haben die Eigenschaft, dass sich ihre Funktionswerte in regelmäßigen Abständen wiederholen. Die Abstände zwischen dem Auftreten der gleichen Funktionswerte werden Periode genannt. Periodische Folgen können als Spezialfälle der periodischen Funktionen verstanden werden.
Reelle periodische Funktionen
Definition
Eine reelle Zahl
ist eine Periode einer in
definierten
Funktion,
wenn gilt:
Die Funktion
ist periodisch, wenn sie mindestens eine Periode
zulässt. Man sagt dann auch,
sei „
-periodisch“.
Eigenschaften der Menge der Perioden und Beispiele
Für die Periode gelten folgende Eigenschaften:
- Ist
eine Periode von
, so ist auch
eine Periode von
;
- Sind
und
zwei Perioden von
, so ist auch
mit
eine Periode von
.
Meist interessiert man sich für die kleinste positive Periode. Diese
existiert für jede nichtkonstante stetige
periodische Funktion. (Eine konstante Funktion ist periodisch mit jeder
beliebigen Periode ungleich 0.) Wenn
eine kleinste positive Periode hat, so sind die Perioden von
die Vielfachen von
.
Im anderen Fall ist die Menge der Perioden von
dicht
in
.
Beispiele
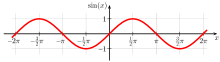
Bekannte periodische Funktionen sind die trigonometrischen Funktionen, insbesondere der Sinus, der eine immer gleich bleibende Schwingung zwischen -1 und 1 durchführt, die sich im Abstand von 2π (π ist die Kreiszahl pi) wiederholt.
Definition
Der Begriff der periodischen Funktion beschränkt sich nicht nur auf reelle Funktionen. Man kann ihn allgemeiner Definieren für Funktionen, auf deren Quellmenge eine Addition erklärt ist.
Sei also
eine (additive) Halbgruppe,
eine Menge
und
eine Funktion. Existiert ein
mit
für alle ,
dann heißt die Funktion
periodisch mit Periode
.
Beispiele
Periodische Folgen
Da eine reelle Folge
eine Funktion von den natürlichen
Zahlen
in die reellen Zahlen
ist, kann der Begriff der periodischen Folge als Spezialfall einer periodischen
Funktion aufgefasst werden. Eine Folge heißt periodische, falls es ein
gibt, so dass für alle
die Gleichheit
gilt. Hierbei wurde ausgenutzt, dass die Menge der natürlichen Zahlen eine
Halbgruppe ist.
Periodische Funktionen als Funktionen auf der Kreislinie
Es sei
der Einheitskreis. Man kann
periodische Funktionen auf
mit Periode
mit Funktionen auf
identifizieren: Einer Funktion
auf
entspricht die
-periodische
Funktion
.
Hierbei ist
eine Funktion auf dem Einheitskreis also einer Teilmenge der komplexen Zahlen.
Eigenschaften der Funktionen wie Beschränktheit, Stetigkeit oder Differenzierbarkeit
übertragen sich jeweils auf die andere Sichtweise.
Beispielsweise entsprechen Fourier-Reihen
unter dieser Abbildung den Laurent-Reihen
.
Periodische Funktionen auf reellen Vektorräumen
Es sei
ein
-dimensionaler
reeller Vektorraum, z.B.
.
Eine Periode einer stetigen, reell- oder komplexwertigen Funktion
auf
oder einem (offenen,
zusammenhängenden)
Teil
von
ist ein Vektor
,
so dass
- der Definitionsbereich
von
invariant unter der Translation mit
ist, d.h.
- für alle
gilt:
.
Die Menge
aller Perioden von
ist eine abgeschlossene
Untergruppe von
.
Jede solche Untergruppe ist die direkte
Summe aus einem Untervektorraum
von
und einer diskreten
Untergruppe; letztere lässt sich beschreiben als die Menge der ganzzahligen Linearkombinationen
einer Menge linear unabhängiger Vektoren.
Wendet man diese Theorie auf den reell zweidimensionalen Vektorraum
an und betrachtet nur holomorphe Funktionen
,
so gibt es die folgenden Fälle:
:
ist nicht periodisch.
:
ist eine gewöhnliche periodische Funktion; beispielsweise ist die Exponentialfunktion periodisch mit Periode
.
enthält einen nichttrivialen reellen Unterraum: Eine holomorphe Funktion, die entlang einer Gerade konstant ist, ist insgesamt konstant.
:
hat zwei reell linear unabhängige Perioden. Ist
auf der ganzen Ebene meromorph, so spricht man von einer elliptischen Funktion.
Siehe auch


© biancahoegel.de;
Datum der letzten Änderung: Jena, den: 25.02. 2020